Problem

Sort an array

Similar Sorts

3-way Merge Sort

Solution

Mergesort is one of the older algorithms known since 1945. It is very good example of divide and conquer paradigm and is better than other simpler sort algorithms like selection, insertion or bubble sort.

Method 1 - Recursive Top Down Merge Sort

Merge sort is a recursive algorithm that repeatedly calls itself on progressively smaller subsets of the problem.

Algorithm

We start by splitting the array into two halves, then sort each half, and finally merge them back together. This splitting continues until the base case of a single-element array is reached, allowing us to exit the recursion.

After reaching the base case, we merge the sorted halves to form the combined array. This merging step combines the two sorted arrays into a single sorted array.

So, this sums up merge sort algorithm:

  1. Divide: Split the array into two halves.
  2. Conquer: Recursively sort each half.
  3. Combine: Merge the two sorted halves into a single sorted array.

Here is a visual representation of merge sort:

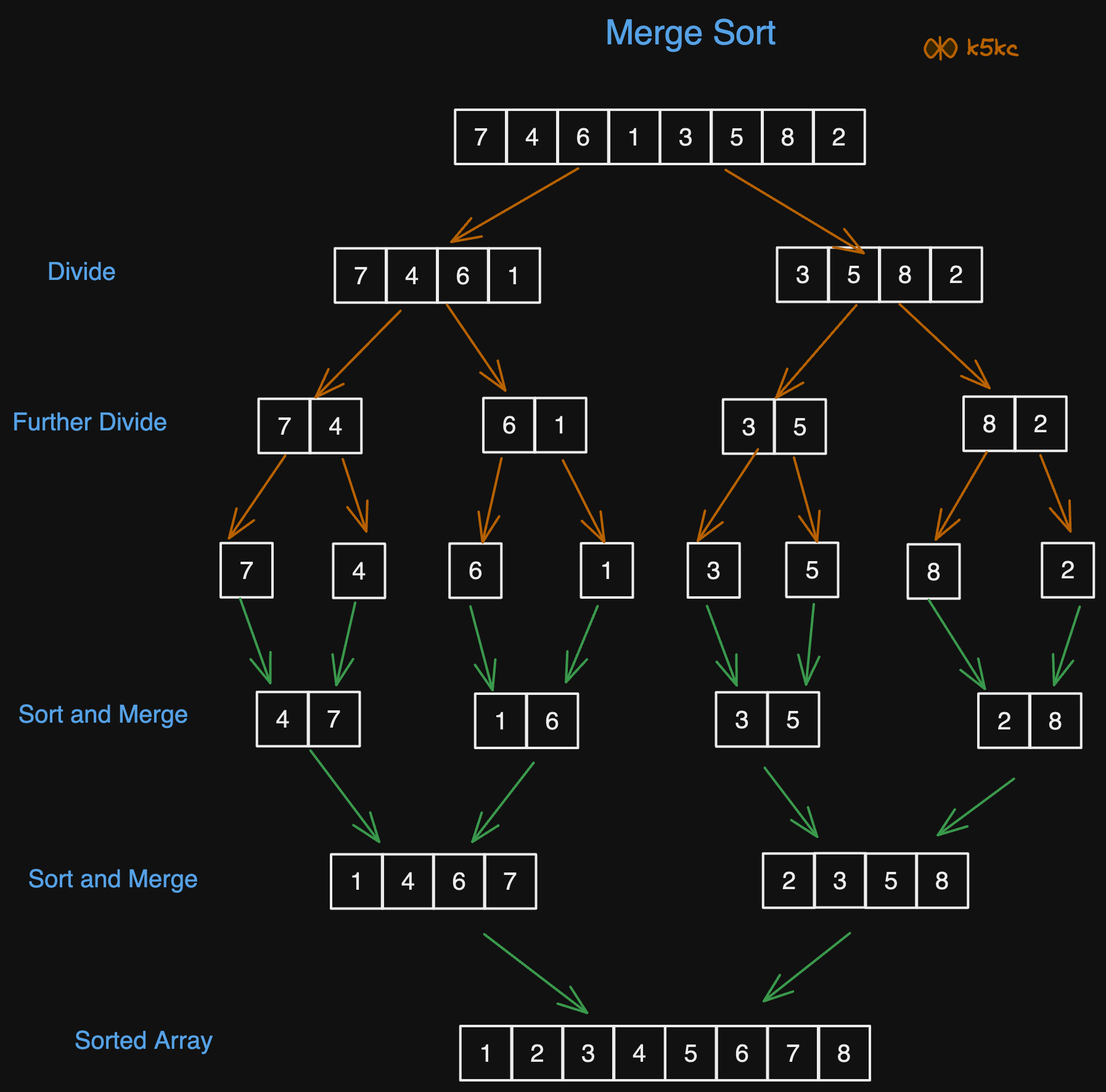
Here is the video explanation:

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

class Solution {
	
	public int[] sortArray(int[] nums) {
		int[] copy = Arrays.copyOf(nums, nums.length);
		mergeSort(copy);
		return copy;
	}
	
	public void mergeSort(int[] nums) {
		mergeSort(nums, 0, nums.length - 1);
	}
	
	// Helper method to sort the array
	private void mergeSort(int[] nums, int left, int right) {
		if (left >= right) {
			return;
		}
		// Find the middle point
		int mid = left + (right - left) / 2;

		// Sort the first half
		mergeSort(nums, left, mid);

		// Sort the second half
		mergeSort(nums, mid + 1, right);

		// Merge the sorted halves
		merge(nums, left, mid, right);
	}

    // Helper method to merge two halves
    private void merge(int[] nums, int left, int mid, int right) {
        // Find sizes of two subarrays to be merged
        int nLeft = mid - left + 1;
        int nRight = right - mid;

        // Create temporary arrays
        int[] leftArr = new int[nLeft];
        int[] rightArr = new int[nRight];

        // Copy data to temporary arrays
        System.arraycopy(nums, left, leftArr, 0, nLeft);
        System.arraycopy(nums, mid + 1, rightArr, 0, nRight);

        // Merge the temporary arrays

        // Initial indexes of first and second subarrays
        int i = 0, j = 0;

        // Initial index of merged subarray array
        int k = left;

        while (i < nLeft && j < nRight) {
            if (leftArr[i] <= rightArr[j]) {
                nums[k] = leftArr[i];
                i++;
            } else {
                nums[k] = rightArr[j];
                j++;
            }

            k++;
        }

        // Copy remaining elements of leftArray if any
        while (i < nLeft) {
            nums[k] = leftArr[i];
            i++;
            k++;
        }

        // Copy remaining elements of rightArray if any
        while (j < nRight) {
            nums[k] = rightArr[j];
            j++;
            k++;
        }
    }


}

Complexity

  • ⏰ Time complexity: O(n log n), where n is number of elements. At each step in recursion, we are splitting array in two halves. This takes O(1) time, but we are doing for log n levels. Then at each step, we are merging the sorted arrays that takes O(n) time, but for all the levels it is O(log n * n)
  • 🧺 Space complexity: O(n), as our recursion stack goes log(n) levels, but at each level we have O(n) sized temporary array.

Method 2 - Iterative or Bottom up Merge Sort

This is iterative solution, of previous recursive method.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

public void mergeSort(int[] nums) {
	for (int size = 1; size < nums.length; size *= 2) {
		for (int i = 0; i < nums.length - size; i += 2 * size) {
			int mid = i + size - 1;
			int end = Math.min(i + 2 * size - 1, nums.length - 1);
			merge(nums, i, mid, end);
		}
	}
}
private void merge(int[] nums, int l, int mid, int r) {
	int[] tmp = new int[r - l + 1];
	int i = l, j = mid + 1, k = 0;
	while (i <= mid || j <= r) {
		if (i > mid || j <= r && nums[i] > nums[j]) {
			tmp[k++] = nums[j++];
		} else {
			tmp[k++] = nums[i++];
		}
	}
	System.arraycopy(tmp, 0, nums, l, r - l + 1);
}

Top Down vs Bottom up Merge Sort

Top down Bottom up
Recursive Non recursive
It is top down, as we break the array into 2 halves, and these halves into further sub halves and so on, sort them and merge again Here we dont break into halves, rather we have a step, which determines the size of the array to be broken. Initially it is one, we sort the array of size equal to step and go further
Has more number of iterations Has lesser number of iterations
Professor Kevin wayne (of Princeton) replied that in many cases recursion is faster than iteration because of caching improved performances. Algorithm wise it is as fast as top down, but may be slower as current implementation provide faster support for recurs

Method 3 - In Place Recursive Merge Sort

In-place Merge Sort is a more challenging variant of the traditional Merge Sort algorithm because the standard merge operation inherently requires additional space proportional to the size of the array. However, it is possible to implement an in-place merge sort, although the implementation is complex and less common due to the complications involved in merging in place.

Here’s an outline of how you can achieve in-place merge sort with some additional complexity:

  1. Divide: Divide the array into two halves.
  2. Conquer: Recursively sort each half.
  3. In-place Combine: Merge the two sorted halves in place without using extra space.

Steps

  1. Divide: This step remains the same as the standard merge sort. Split the array into two halves.
  2. Recursive Sort: Recursively sort both halves.
  3. In-place Merge: To merge two sorted halves in place, you can use a technique known as the binary insertion method or rotate-and-swap operations to avoid additional space.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

public class InPlaceMergeSort {

	public static void main(String[] args) {
		int[] nums = { 38, 27, 43, 3, 9, 82, 10 };
		mergeSort(nums, 0, nums.length - 1);

		System.out.println("Sorted array:");

		for (int num: nums) {
			System.out.print(num + " ");
		}
	}

	public static void mergeSort(int[] array, int left, int right) {
		if (left < right) {
			int middle = left + (right - left) / 2;

			// Sort first and second halves
			mergeSort(array, left, middle);
			mergeSort(array, middle + 1, right);

			// Merge the sorted halves
			mergeInPlace(array, left, middle, right);
		}
	}

	public static void mergeInPlace(int[] array, int left, int middle, int right) {
		int start2 = middle + 1;

		// If the direct merge is already sorted
		if (array[middle] <= array[start2]) {
			return;
		}

		// Two pointers to maintain start
		// of both arrays to merge
		while (left <= middle && start2  < = right) {

			// If element 1 is in right place
			if (array[left] <= array[start2]) {
				left++;
			} else {
				int value = array[start2];
				int index = start2;

				// Shift all the elements between element 1
				// element 2, right by 1.
				while (index != left) {
					array[index] = array[index - 1];
					index--;
				}

				array[left] = value;

				// Update all the pointers
				left++;
				middle++;
				start2++;
			}
		}
	}
}

Complexity

  • ⏰ Time complexity: O(n log n)
  • 🧺 Space complexity: O(1), The space complexity improves to O(1) in terms of extra space for merging, but this also comes with increased complexity in the merging process.

Complexity Summary

Note
Best Time: O(n log n) Merge operation on every step
Average Time: O(n log n) Same as above
Worst Time: O(n log n) Same as above
Stability: Stable
In-place: No
Best Space: O(n) Requires splitting list into new ones
Average Space: O(n) Same as above
Worst Space: O(n) Same as above