Middle of the linked list

Problem

Given the head of a singly linked list, return the middle node of the linked list.

If there are two middle nodes, return the second middle node.

Examples

Example 1:

graph LR
    A(1) --> B(2) --> C(3):::RedNode --> D(4) --> E(5)

classDef RedNode fill:#ff0000;

Input: head = [1,2,3,4,5]
Output: [3,4,5]
Explanation: The middle node of the list is node 3.

Example 2:

graph LR
    F(1) --> G(2) --> H(3) --> I(4):::RedNode --> J(5) -->K(6)

classDef RedNode fill:#ff0000;

Input: head = [1,2,3,4,5,6]
Output: [4,5,6]
Explanation: Since the list has two middle nodes with values 3 and 4, we return the second one.

Follow up

Follow up - How will you get it in first pass.

Constraints

• The number of nodes in the list is in the range [1, 100].
• 1 <= Node.val <= 100

Solution

Video explanation

Here is the video explaining below methods in detail. Please check it out:

<div class="youtube-embed"><iframe src="https://www.youtube.com/embed/hW8Qvt_jonw" frameborder="0" allowfullscreen></iframe></div>

Method 1 - Get the Length and Travel to Middle

Traverse the whole linked list and count the no. of nodes. Now traverse the list again till count/2 and return the node at count/2.

Code

Java

class Solution {
    public ListNode middleNode(ListNode head) {
        // Step 1: Calculate the length of the list
        int length = 0;
        ListNode current = head;
        while (current != null) {
            length++;
            current = current.next;
        }
        
        // Step 2: Find the middle node's position
        int mid = length / 2;
        
        // Step 3: Traverse to the middle node
        current = head;
        for (int i = 0; i < mid; i++) {
            current = current.next;
        }
        
        return current;
    }
}

Python

class Solution:
    def middleNode(self, head: Optional[ListNode]) -> Optional[ListNode]:
        # Step 1: Calculate the length of the list
        length = 0
        current = head
        while current:
            length += 1
            current = current.next
        
        # Step 2: Find the middle node's position
        mid = length // 2
        
        # Step 3: Traverse to the middle node
        current = head
        for _ in range(mid):
            current = current.next
        
        return current

Complexity

• ⏰ Time complexity: O(n), where n is length of linked list.
• 🧺 Space complexity: O(1)

Method 2 - Uses One Slow Pointer and One Fast Pointer 🏆

Traverse linked list using two pointers. Move one pointer by one and other pointer by two. When the fast pointer reaches end slow pointer will reach middle of the linked list. This is done in single pass.

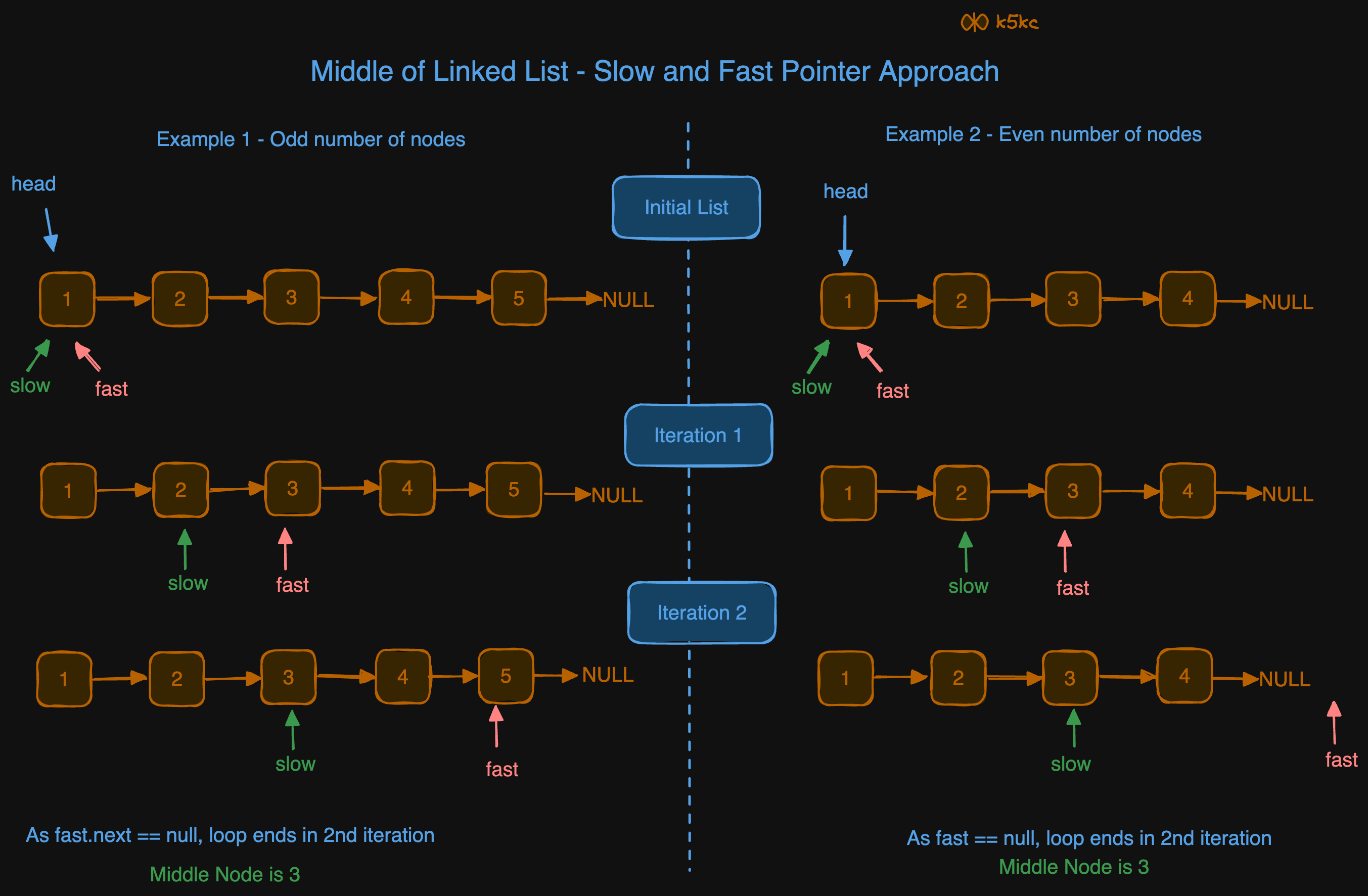
Code

Java

class Solution {
	public ListNode middleNode(ListNode head) {
		ListNode fast = head, slow = head;
	
		while (fast != null && fast.next != null) {
			fast = fast.next.next;
			slow = slow.next;
		}
	
		return slow;
	}
}

Python

class Solution:
    def middleNode(self, head: Optional[ListNode]) -> Optional[ListNode]:
        slow, fast = head, head
        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next
        return slow

Method 3 - Using a Counter

Initialize mid element as head and initialize a counter as 0. Traverse the list from head, while traversing increment the counter and change mid to mid->next whenever the counter is odd. So the mid will move only half of the total length of the list.

Code

C

mynode * getTheMiddle(mynode * head) {
	mynode * middle = (mynode * ) NULL;
	int i;

	for (i = 1; head != (mynode * ) NULL; head = head -> next, i++) {
		if (i == 1)
			middle = head;
		else if ((i % 2) == 1)
			middle = middle -> next;
	}

	return middle;
}