problemeasyalgorithmsleetcode-2293leetcode 2293leetcode2293

Min Max Game

EasyUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given a 0-indexed integer array nums whose length is a power of 2.

Apply the following algorithm on nums:

  1. Let n be the length of nums. If n == 1, end the process. Otherwise, create a new 0-indexed integer array newNums of length n / 2.
  2. For every even index i where 0 <= i < n / 2, assign the value of newNums[i] as min(nums[2 * i], nums[2 * i + 1]).
  3. For every odd index i where 0 <= i < n / 2, assign the value of newNums[i] as max(nums[2 * i], nums[2 * i + 1]).
  4. Replace the array nums with newNums.
  5. Repeat the entire process starting from step 1.

Return the last number that remains innums after applying the algorithm.

Examples

Example 1


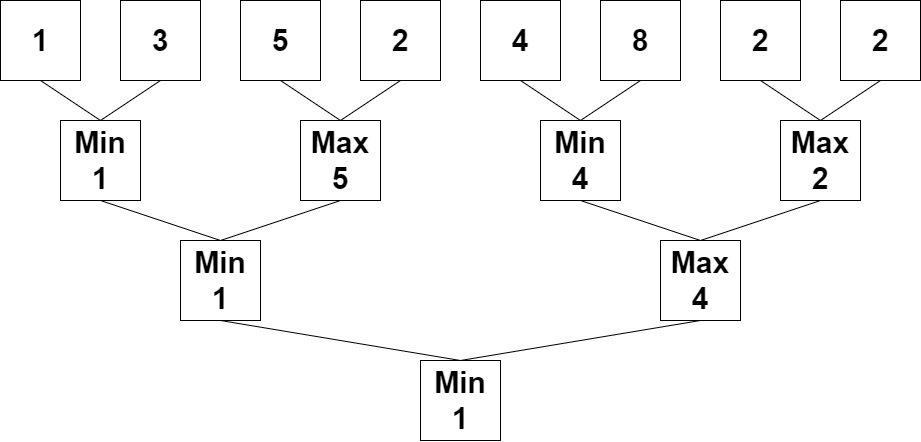
![](https://assets.leetcode.com/uploads/2022/04/13/example1drawio-1.png)

Input: nums = [1,3,5,2,4,8,2,2]
Output: 1
Explanation: The following arrays are the results of applying the algorithm repeatedly.
First: nums = [1,5,4,2]
Second: nums = [1,4]
Third: nums = [1]
1 is the last remaining number, so we return 1.

Example 2

Input: nums = [3]
Output: 3
Explanation: 3 is already the last remaining number, so we return 3.

Constraints

  • 1 <= nums.length <= 10^24
  • 1 <= nums[i] <= 10^9
  • nums.length is a power of 2.

Solution

Method 1 – Simulation with Array Reduction

Intuition

The process repeatedly reduces the array by applying min or max to pairs of elements, alternating between min for even indices and max for odd indices. This continues until only one element remains.

Approach

  1. While the array has more than one element:
    • Create a new array of half the size.
    • For each index i in the new array:
      • If i is even, set newNums[i] = min(nums[2*i], nums[2*i+1]).
      • If i is odd, set newNums[i] = max(nums[2*i], nums[2*i+1]).
    • Replace nums with newNums.
  2. Return the single remaining element.

Code

C++
class Solution {
public:
    int minMaxGame(vector<int>& nums) {
        while (nums.size() > 1) {
            vector<int> newNums(nums.size() / 2);
            for (int i = 0; i < newNums.size(); ++i) {
                if (i % 2 == 0) newNums[i] = min(nums[2*i], nums[2*i+1]);
                else newNums[i] = max(nums[2*i], nums[2*i+1]);
            }
            nums = newNums;
        }
        return nums[0];
    }
};
Go
func minMaxGame(nums []int) int {
    for len(nums) > 1 {
        n := len(nums) / 2
        newNums := make([]int, n)
        for i := 0; i < n; i++ {
            if i%2 == 0 {
                newNums[i] = min(nums[2*i], nums[2*i+1])
            } else {
                newNums[i] = max(nums[2*i], nums[2*i+1])
            }
        }
        nums = newNums
    }
    return nums[0]
}
func min(a, b int) int { if a < b { return a } else { return b } }
func max(a, b int) int { if a > b { return a } else { return b } }
Java
class Solution {
    public int minMaxGame(int[] nums) {
        while (nums.length > 1) {
            int n = nums.length / 2;
            int[] newNums = new int[n];
            for (int i = 0; i < n; i++) {
                if (i % 2 == 0) newNums[i] = Math.min(nums[2*i], nums[2*i+1]);
                else newNums[i] = Math.max(nums[2*i], nums[2*i+1]);
            }
            nums = newNums;
        }
        return nums[0];
    }
}
Kotlin
class Solution {
    fun minMaxGame(nums: IntArray): Int {
        var arr = nums
        while (arr.size > 1) {
            val n = arr.size / 2
            val newArr = IntArray(n)
            for (i in 0 until n) {
                newArr[i] = if (i % 2 == 0) minOf(arr[2*i], arr[2*i+1]) else maxOf(arr[2*i], arr[2*i+1])
            }
            arr = newArr
        }
        return arr[0]
    }
}
Python
def min_max_game(nums: list[int]) -> int:
    while len(nums) > 1:
        new_nums = []
        for i in range(len(nums) // 2):
            if i % 2 == 0:
                new_nums.append(min(nums[2*i], nums[2*i+1]))
            else:
                new_nums.append(max(nums[2*i], nums[2*i+1]))
        nums = new_nums
    return nums[0]
Rust
impl Solution {
    pub fn min_max_game(mut nums: Vec<i32>) -> i32 {
        while nums.len() > 1 {
            let n = nums.len() / 2;
            let mut new_nums = vec![0; n];
            for i in 0..n {
                new_nums[i] = if i % 2 == 0 {
                    nums[2*i].min(nums[2*i+1])
                } else {
                    nums[2*i].max(nums[2*i+1])
                };
            }
            nums = new_nums;
        }
        nums[0]
    }
}
TypeScript
class Solution {
    minMaxGame(nums: number[]): number {
        while (nums.length > 1) {
            const n = nums.length / 2;
            const newNums: number[] = [];
            for (let i = 0; i < n; ++i) {
                if (i % 2 === 0) newNums.push(Math.min(nums[2*i], nums[2*i+1]));
                else newNums.push(Math.max(nums[2*i], nums[2*i+1]));
            }
            nums = newNums;
        }
        return nums[0];
    }
}

Complexity

  • ⏰ Time complexity: O(n), each round halves the array size.
  • 🧺 Space complexity: O(n), for the temporary arrays.

Comments