Minesweeper
MediumUpdated: Aug 2, 2025
Practice on:
Problem
Let's play the minesweeper game (Wikipedia, online game)!
You are given an m x n char matrix board representing the game board where:
'M'represents an unrevealed mine,'E'represents an unrevealed empty square,'B'represents a revealed blank square that has no adjacent mines (i.e., above, below, left, right, and all 4 diagonals),- digit (
'1'to'8') represents how many mines are adjacent to this revealed square, and 'X'represents a revealed mine.
You are also given an integer array click where click = [clickr, clickc]
represents the next click position among all the unrevealed squares ('M' or
'E').
Return the board after revealing this position according to the following rules :
- If a mine
'M'is revealed, then the game is over. You should change it to'X'. - If an empty square
'E'with no adjacent mines is revealed, then change it to a revealed blank'B'and all of its adjacent unrevealed squares should be revealed recursively. - If an empty square
'E'with at least one adjacent mine is revealed, then change it to a digit ('1'to'8') representing the number of adjacent mines. - Return the board when no more squares will be revealed.
Examples
Example 1
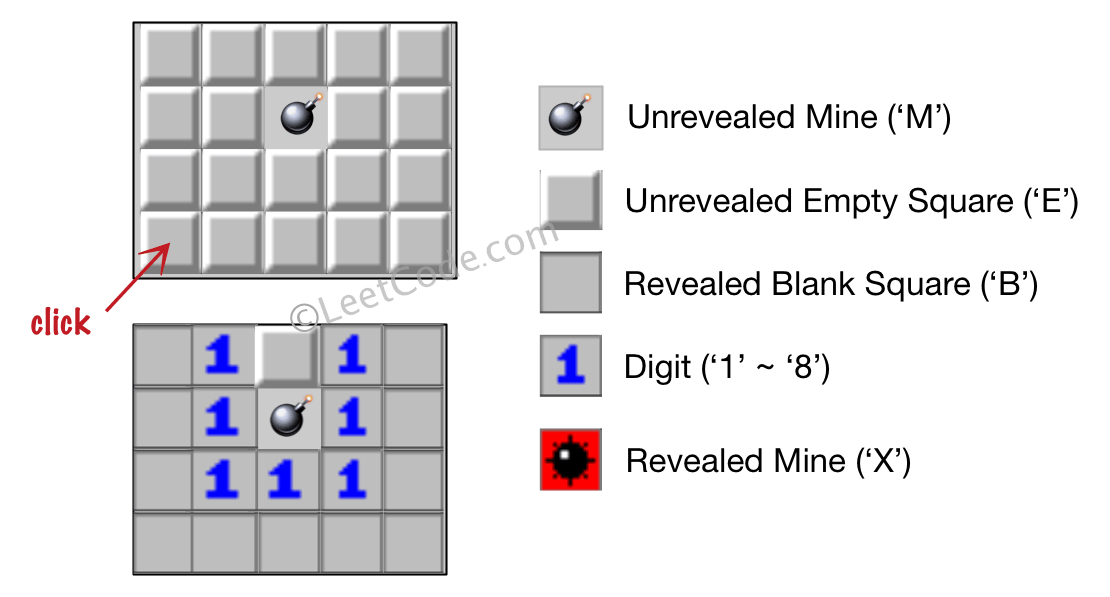
Input: board = [["E","E","E","E","E"],["E","E","M","E","E"],["E","E","E","E","E"],["E","E","E","E","E"]], click = [3,0]
Output: [["B","1","E","1","B"],["B","1","M","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]]
Example 2
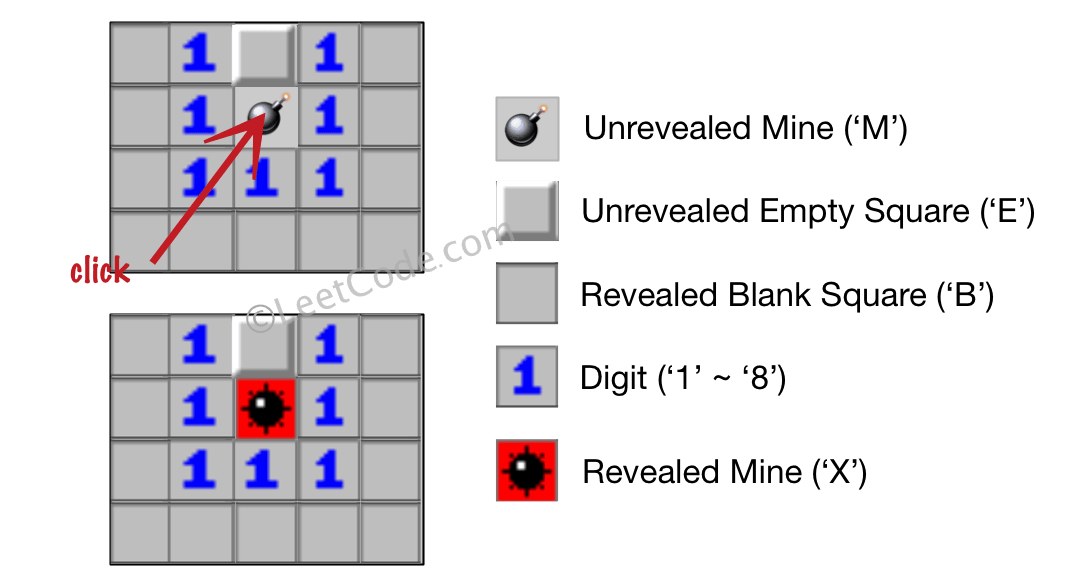
Input: board = [["B","1","E","1","B"],["B","1","M","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]], click = [1,2]
Output: [["B","1","E","1","B"],["B","1","X","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]]
Constraints
m == board.lengthn == board[i].length1 <= m, n <= 50board[i][j]is either'M','E','B', or a digit from'1'to'8'.click.length == 20 <= clickr < m0 <= clickc < nboard[clickr][clickc]is either'M'or'E'.
Solution
Method 1 – Depth-First Search (DFS)
Intuition
To reveal cells in Minesweeper, use DFS to uncover empty cells and recursively reveal their neighbors if they have no adjacent mines. If a cell is adjacent to mines, mark it with the count; if it's a mine, mark it as 'X'.
Approach
- If the clicked cell is a mine ('M'), change it to 'X' and return the board.
- Otherwise, start DFS from the clicked cell:
- Count adjacent mines.
- If count > 0, mark cell with the count.
- If count == 0, mark cell as 'B' and recursively reveal all adjacent unrevealed cells.
- Use directions to check all 8 neighbors.
- Return the updated board.
Code
C++
class Solution {
public:
vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click) {
int m = board.size(), n = board[0].size();
vector<pair<int, int>> dirs = {{-1,-1},{-1,0},{-1,1},{0,-1},{0,1},{1,-1},{1,0},{1,1}};
function<void(int,int)> dfs = [&](int x, int y) {
if (x < 0 || x >= m || y < 0 || y >= n || board[x][y] != 'E') return;
int cnt = 0;
for (auto& d : dirs) {
int nx = x + d.first, ny = y + d.second;
if (nx >= 0 && nx < m && ny >= 0 && ny < n && board[nx][ny] == 'M') cnt++;
}
if (cnt) board[x][y] = '0' + cnt;
else {
board[x][y] = 'B';
for (auto& d : dirs) dfs(x + d.first, y + d.second);
}
};
int x = click[0], y = click[1];
if (board[x][y] == 'M') board[x][y] = 'X';
else dfs(x, y);
return board;
}
};
Go
func updateBoard(board [][]byte, click []int) [][]byte {
m, n := len(board), len(board[0])
dirs := [8][2]int{{-1,-1},{-1,0},{-1,1},{0,-1},{0,1},{1,-1},{1,0},{1,1}}
var dfs func(x, y int)
dfs = func(x, y int) {
if x < 0 || x >= m || y < 0 || y >= n || board[x][y] != 'E' { return }
cnt := 0
for _, d := range dirs {
nx, ny := x+d[0], y+d[1]
if nx >= 0 && nx < m && ny >= 0 && ny < n && board[nx][ny] == 'M' { cnt++ }
}
if cnt > 0 {
board[x][y] = byte('0' + cnt)
} else {
board[x][y] = 'B'
for _, d := range dirs {
dfs(x+d[0], y+d[1])
}
}
}
x, y := click[0], click[1]
if board[x][y] == 'M' {
board[x][y] = 'X'
} else {
dfs(x, y)
}
return board
}
Java
class Solution {
int[][] dirs = {{-1,-1},{-1,0},{-1,1},{0,-1},{0,1},{1,-1},{1,0},{1,1}};
public char[][] updateBoard(char[][] board, int[] click) {
int m = board.length, n = board[0].length;
int x = click[0], y = click[1];
if (board[x][y] == 'M') {
board[x][y] = 'X';
return board;
}
dfs(board, x, y, m, n);
return board;
}
void dfs(char[][] board, int x, int y, int m, int n) {
if (x < 0 || x >= m || y < 0 || y >= n || board[x][y] != 'E') return;
int cnt = 0;
for (int[] d : dirs) {
int nx = x + d[0], ny = y + d[1];
if (nx >= 0 && nx < m && ny >= 0 && ny < n && board[nx][ny] == 'M') cnt++;
}
if (cnt > 0) board[x][y] = (char)('0' + cnt);
else {
board[x][y] = 'B';
for (int[] d : dirs) dfs(board, x + d[0], y + d[1], m, n);
}
}
}
Kotlin
class Solution {
val dirs = arrayOf(
intArrayOf(-1,-1), intArrayOf(-1,0), intArrayOf(-1,1),
intArrayOf(0,-1), intArrayOf(0,1), intArrayOf(1,-1), intArrayOf(1,0), intArrayOf(1,1)
)
fun updateBoard(board: Array<CharArray>, click: IntArray): Array<CharArray> {
val m = board.size; val n = board[0].size
val x = click[0]; val y = click[1]
if (board[x][y] == 'M') {
board[x][y] = 'X'
return board
}
fun dfs(x: Int, y: Int) {
if (x !in 0 until m || y !in 0 until n || board[x][y] != 'E') return
var cnt = 0
for (d in dirs) {
val nx = x + d[0]; val ny = y + d[1]
if (nx in 0 until m && ny in 0 until n && board[nx][ny] == 'M') cnt++
}
if (cnt > 0) board[x][y] = ('0' + cnt)
else {
board[x][y] = 'B'
for (d in dirs) dfs(x + d[0], y + d[1])
}
}
dfs(x, y)
return board
}
}
Python
def update_board(board: list[list[str]], click: list[int]) -> list[list[str]]:
m, n = len(board), len(board[0])
dirs = [(-1,-1),(-1,0),(-1,1),(0,-1),(0,1),(1,-1),(1,0),(1,1)]
def dfs(x: int, y: int):
if not (0 <= x < m and 0 <= y < n) or board[x][y] != 'E': return
cnt = 0
for dx, dy in dirs:
nx, ny = x + dx, y + dy
if 0 <= nx < m and 0 <= ny < n and board[nx][ny] == 'M':
cnt += 1
if cnt:
board[x][y] = str(cnt)
else:
board[x][y] = 'B'
for dx, dy in dirs:
dfs(x + dx, y + dy)
x, y = click
if board[x][y] == 'M':
board[x][y] = 'X'
else:
dfs(x, y)
return board
Rust
impl Solution {
pub fn update_board(board: &mut Vec<Vec<char>>, click: Vec<i32>) -> &mut Vec<Vec<char>> {
let m = board.len();
let n = board[0].len();
let dirs = [(-1,-1),(-1,0),(-1,1),(0,-1),(0,1),(1,-1),(1,0),(1,1)];
fn dfs(board: &mut Vec<Vec<char>>, x: i32, y: i32, m: usize, n: usize, dirs: &[(i32,i32);8]) {
if x < 0 || x >= m as i32 || y < 0 || y >= n as i32 || board[x as usize][y as usize] != 'E' { return; }
let mut cnt = 0;
for &(dx, dy) in dirs {
let nx = x + dx; let ny = y + dy;
if nx >= 0 && nx < m as i32 && ny >= 0 && ny < n as i32 && board[nx as usize][ny as usize] == 'M' {
cnt += 1;
}
}
if cnt > 0 {
board[x as usize][y as usize] = (b'0' + cnt as u8) as char;
} else {
board[x as usize][y as usize] = 'B';
for &(dx, dy) in dirs {
dfs(board, x + dx, y + dy, m, n, dirs);
}
}
}
let x = click[0] as i32; let y = click[1] as i32;
if board[x as usize][y as usize] == 'M' {
board[x as usize][y as usize] = 'X';
} else {
dfs(board, x, y, m, n, &dirs);
}
board
}
}
TypeScript
class Solution {
updateBoard(board: string[][], click: number[]): string[][] {
const m = board.length, n = board[0].length;
const dirs = [[-1,-1],[-1,0],[-1,1],[0,-1],[0,1],[1,-1],[1,0],[1,1]];
function dfs(x: number, y: number) {
if (x < 0 || x >= m || y < 0 || y >= n || board[x][y] !== 'E') return;
let cnt = 0;
for (const [dx, dy] of dirs) {
const nx = x + dx, ny = y + dy;
if (nx >= 0 && nx < m && ny >= 0 && ny < n && board[nx][ny] === 'M') cnt++;
}
if (cnt > 0) board[x][y] = cnt.toString();
else {
board[x][y] = 'B';
for (const [dx, dy] of dirs) dfs(x + dx, y + dy);
}
}
const [x, y] = click;
if (board[x][y] === 'M') board[x][y] = 'X';
else dfs(x, y);
return board;
}
}
Complexity
- ⏰ Time complexity:
O(mn), each cell is visited at most once. - 🧺 Space complexity:
O(mn), for recursion stack in worst case.