Problem

You are given an m x n integer matrix grid containing distinct positive integers.

You have to replace each integer in the matrix with a positive integer satisfying the following conditions:

  • The relative order of every two elements that are in the same row or column should stay the same after the replacements.
  • The maximum number in the matrix after the replacements should be as small as possible.

The relative order stays the same if for all pairs of elements in the original matrix such that grid[r1][c1] > grid[r2][c2] where either r1 == r2 or c1 == c2, then it must be true that grid[r1][c1] > grid[r2][c2] after the replacements.

For example, if grid = [[2, 4, 5], [7, 3, 9]] then a good replacement could be either grid = [[1, 2, 3], [2, 1, 4]] or grid = [[1, 2, 3], [3, 1, 4]].

Return theresulting matrix. If there are multiple answers, return any of them.

Examples

Example 1:

1
2
3
4
5

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2300-2399/2371.Minimize%20Maximum%20Value%20in%20a%20Grid/images/grid2drawio.png)
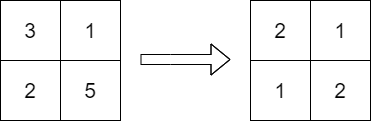
Input: grid = [[3,1],[2,5]]
Output: [[2,1],[1,2]]
Explanation: The above diagram shows a valid replacement.
The maximum number in the matrix is 2. It can be shown that no smaller value can be obtained.

Example 2:

1
2
3

Input: grid = [[10]]
Output: [[1]]
Explanation: We replace the only number in the matrix with 1.

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 1000
  • 1 <= m * n <= 10^5
  • 1 <= grid[i][j] <= 10^9
  • grid consists of distinct integers.

Solution

Method 1 – Topological Sort with Greedy Assignment

Intuition

To minimize the maximum value after replacements while preserving the relative order in each row and column, treat each cell as a node in a directed graph. Add edges for each row and column according to the original order. Use topological sorting to assign the smallest possible values to each cell, ensuring all constraints are satisfied.

Approach

  1. For each row and column, add directed edges from larger to smaller values according to the original grid.
  2. Build a graph and compute in-degrees for all cells.
  3. Use Kahn’s algorithm for topological sorting:
    • Start with cells having zero in-degree.
    • Assign the next smallest available value to each cell as it is processed.
    • Decrease in-degree of neighbors and add them to the queue when their in-degree becomes zero.
  4. The largest assigned value is the minimized maximum value.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

class Solution {
public:
    int minimizeMaxValue(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> ans(m, vector<int>(n));
        vector<vector<int>> indeg(m, vector<int>(n));
        vector<vector<vector<pair<int,int>>>> g(m, vector<vector<pair<int,int>>>(n));
        // Build graph for rows
        for (int i = 0; i < m; ++i) {
            vector<pair<int,int>> row;
            for (int j = 0; j < n; ++j) row.push_back({grid[i][j], j});
            sort(row.begin(), row.end());
            for (int k = 1; k < n; ++k) {
                g[i][row[k-1].second].push_back({i, row[k].second});
                indeg[i][row[k].second]++;
            }
        }
        // Build graph for columns
        for (int j = 0; j < n; ++j) {
            vector<pair<int,int>> col;
            for (int i = 0; i < m; ++i) col.push_back({grid[i][j], i});
            sort(col.begin(), col.end());
            for (int k = 1; k < m; ++k) {
                g[col[k-1].second][j].push_back({col[k].second, j});
                indeg[col[k].second][j]++;
            }
        }
        queue<pair<int,int>> q;
        for (int i = 0; i < m; ++i) for (int j = 0; j < n; ++j) if (indeg[i][j] == 0) q.push({i,j});
        int val = 1;
        while (!q.empty()) {
            auto [x, y] = q.front(); q.pop();
            ans[x][y] = val++;
            for (auto& [nx, ny] : g[x][y]) {
                if (--indeg[nx][ny] == 0) q.push({nx, ny});
            }
        }
        int mx = 0;
        for (int i = 0; i < m; ++i) for (int j = 0; j < n; ++j) mx = max(mx, ans[i][j]);
        return mx;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

func minimizeMaxValue(grid [][]int) int {
    m, n := len(grid), len(grid[0])
    ans := make([][]int, m)
    indeg := make([][]int, m)
    g := make([][][][2]int, m)
    for i := range ans {
        ans[i] = make([]int, n)
        indeg[i] = make([]int, n)
        g[i] = make([][][2]int, n)
    }
    for i := 0; i < m; i++ {
        row := make([][2]int, n)
        for j := 0; j < n; j++ { row[j] = [2]int{grid[i][j], j} }
        sort.Slice(row, func(a, b int) bool { return row[a][0] < row[b][0] })
        for k := 1; k < n; k++ {
            g[i][row[k-1][1]] = append(g[i][row[k-1][1]], [2]int{i, row[k][1]})
            indeg[i][row[k][1]]++
        }
    }
    for j := 0; j < n; j++ {
        col := make([][2]int, m)
        for i := 0; i < m; i++ { col[i] = [2]int{grid[i][j], i} }
        sort.Slice(col, func(a, b int) bool { return col[a][0] < col[b][0] })
        for k := 1; k < m; k++ {
            g[col[k-1][1]][j] = append(g[col[k-1][1]][j], [2]int{col[k][1], j})
            indeg[col[k][1]][j]++
        }
    }
    q := [][2]int{}
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if indeg[i][j] == 0 {
                q = append(q, [2]int{i, j})
            }
        }
    }
    val := 1
    for len(q) > 0 {
        x, y := q[0][0], q[0][1]
        q = q[1:]
        ans[x][y] = val
        val++
        for _, nb := range g[x][y] {
            nx, ny := nb[0], nb[1]
            indeg[nx][ny]--
            if indeg[nx][ny] == 0 {
                q = append(q, [2]int{nx, ny})
            }
        }
    }
    mx := 0
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if ans[i][j] > mx { mx = ans[i][j] }
        }
    }
    return mx
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

class Solution {
    public int minimizeMaxValue(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int[][] ans = new int[m][n];
        int[][] indeg = new int[m][n];
        List<int[]>[][] g = new ArrayList[m][n];
        for (int i = 0; i < m; i++) for (int j = 0; j < n; j++) g[i][j] = new ArrayList<>();
        for (int i = 0; i < m; i++) {
            int[][] row = new int[n][2];
            for (int j = 0; j < n; j++) row[j] = new int[]{grid[i][j], j};
            Arrays.sort(row, Comparator.comparingInt(a -> a[0]));
            for (int k = 1; k < n; k++) {
                g[i][row[k-1][1]].add(new int[]{i, row[k][1]});
                indeg[i][row[k][1]]++;
            }
        }
        for (int j = 0; j < n; j++) {
            int[][] col = new int[m][2];
            for (int i = 0; i < m; i++) col[i] = new int[]{grid[i][j], i};
            Arrays.sort(col, Comparator.comparingInt(a -> a[0]));
            for (int k = 1; k < m; k++) {
                g[col[k-1][1]][j].add(new int[]{col[k][1], j});
                indeg[col[k][1]][j]++;
            }
        }
        Queue<int[]> q = new LinkedList<>();
        for (int i = 0; i < m; i++) for (int j = 0; j < n; j++) if (indeg[i][j] == 0) q.offer(new int[]{i, j});
        int val = 1;
        while (!q.isEmpty()) {
            int[] cur = q.poll();
            int x = cur[0], y = cur[1];
            ans[x][y] = val++;
            for (int[] nb : g[x][y]) {
                int nx = nb[0], ny = nb[1];
                if (--indeg[nx][ny] == 0) q.offer(new int[]{nx, ny});
            }
        }
        int mx = 0;
        for (int i = 0; i < m; i++) for (int j = 0; j < n; j++) mx = Math.max(mx, ans[i][j]);
        return mx;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

class Solution {
    fun minimizeMaxValue(grid: Array<IntArray>): Int {
        val m = grid.size; val n = grid[0].size
        val ans = Array(m) { IntArray(n) }
        val indeg = Array(m) { IntArray(n) }
        val g = Array(m) { Array(n) { mutableListOf<Pair<Int,Int>>() } }
        for (i in 0 until m) {
            val row = Array(n) { j -> grid[i][j] to j }
            row.sortBy { it.first }
            for (k in 1 until n) {
                g[i][row[k-1].second].add(i to row[k].second)
                indeg[i][row[k].second]++
            }
        }
        for (j in 0 until n) {
            val col = Array(m) { i -> grid[i][j] to i }
            col.sortBy { it.first }
            for (k in 1 until m) {
                g[col[k-1].second][j].add(col[k].second to j)
                indeg[col[k].second][j]++
            }
        }
        val q = ArrayDeque<Pair<Int,Int>>()
        for (i in 0 until m) for (j in 0 until n) if (indeg[i][j] == 0) q.add(i to j)
        var valNum = 1
        while (q.isNotEmpty()) {
            val (x, y) = q.removeFirst()
            ans[x][y] = valNum++
            for ((nx, ny) in g[x][y]) {
                indeg[nx][ny]--
                if (indeg[nx][ny] == 0) q.add(nx to ny)
            }
        }
        var mx = 0
        for (i in 0 until m) for (j in 0 until n) mx = maxOf(mx, ans[i][j])
        return mx
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

def minimize_max_value(grid: list[list[int]]) -> int:
    from collections import deque
    m, n = len(grid), len(grid[0])
    ans = [[0]*n for _ in range(m)]
    indeg = [[0]*n for _ in range(m)]
    g = [[[] for _ in range(n)] for _ in range(m)]
    for i in range(m):
        row = sorted([(grid[i][j], j) for j in range(n)])
        for k in range(1, n):
            g[i][row[k-1][1]].append((i, row[k][1]))
            indeg[i][row[k][1]] += 1
    for j in range(n):
        col = sorted([(grid[i][j], i) for i in range(m)])
        for k in range(1, m):
            g[col[k-1][1]][j].append((col[k][1], j))
            indeg[col[k][1]][j] += 1
    q = deque()
    for i in range(m):
        for j in range(n):
            if indeg[i][j] == 0:
                q.append((i, j))
    val = 1
    while q:
        x, y = q.popleft()
        ans[x][y] = val
        val += 1
        for nx, ny in g[x][y]:
            indeg[nx][ny] -= 1
            if indeg[nx][ny] == 0:
                q.append((nx, ny))
    mx = 0
    for i in range(m):
        for j in range(n):
            mx = max(mx, ans[i][j])
    return mx
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

impl Solution {
    pub fn minimize_max_value(grid: Vec<Vec<i32>>) -> i32 {
        use std::collections::VecDeque;
        let m = grid.len();
        let n = grid[0].len();
        let mut ans = vec![vec![0; n]; m];
        let mut indeg = vec![vec![0; n]; m];
        let mut g = vec![vec![vec![]; n]; m];
        for i in 0..m {
            let mut row: Vec<(i32, usize)> = (0..n).map(|j| (grid[i][j], j)).collect();
            row.sort();
            for k in 1..n {
                g[i][row[k-1].1].push((i, row[k].1));
                indeg[i][row[k].1] += 1;
            }
        }
        for j in 0..n {
            let mut col: Vec<(i32, usize)> = (0..m).map(|i| (grid[i][j], i)).collect();
            col.sort();
            for k in 1..m {
                g[col[k-1].1][j].push((col[k].1, j));
                indeg[col[k].1][j] += 1;
            }
        }
        let mut q = VecDeque::new();
        for i in 0..m {
            for j in 0..n {
                if indeg[i][j] == 0 {
                    q.push_back((i, j));
                }
            }
        }
        let mut val = 1;
        while let Some((x, y)) = q.pop_front() {
            ans[x][y] = val;
            val += 1;
            for &(nx, ny) in &g[x][y] {
                indeg[nx][ny] -= 1;
                if indeg[nx][ny] == 0 {
                    q.push_back((nx, ny));
                }
            }
        }
        let mut mx = 0;
        for i in 0..m {
            for j in 0..n {
                mx = mx.max(ans[i][j]);
            }
        }
        mx
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

class Solution {
    minimizeMaxValue(grid: number[][]): number {
        const m = grid.length, n = grid[0].length;
        const ans = Array.from({ length: m }, () => Array(n).fill(0));
        const indeg = Array.from({ length: m }, () => Array(n).fill(0));
        const g = Array.from({ length: m }, () => Array.from({ length: n }, () => []));
        for (let i = 0; i < m; ++i) {
            const row = Array.from({ length: n }, (_, j) => [grid[i][j], j]).sort((a, b) => a[0] - b[0]);
            for (let k = 1; k < n; ++k) {
                g[i][row[k-1][1]].push([i, row[k][1]]);
                indeg[i][row[k][1]]++;
            }
        }
        for (let j = 0; j < n; ++j) {
            const col = Array.from({ length: m }, (_, i) => [grid[i][j], i]).sort((a, b) => a[0] - b[0]);
            for (let k = 1; k < m; ++k) {
                g[col[k-1][1]][j].push([col[k][1], j]);
                indeg[col[k][1]][j]++;
            }
        }
        const q = [];
        for (let i = 0; i < m; ++i) for (let j = 0; j < n; ++j) if (indeg[i][j] === 0) q.push([i, j]);
        let val = 1;
        while (q.length) {
            const [x, y] = q.shift();
            ans[x][y] = val++;
            for (const [nx, ny] of g[x][y]) {
                if (--indeg[nx][ny] === 0) q.push([nx, ny]);
            }
        }
        let mx = 0;
        for (let i = 0; i < m; ++i) for (let j = 0; j < n; ++j) mx = Math.max(mx, ans[i][j]);
        return mx;
    }
}

Complexity

  • ⏰ Time complexity: O(mn log(mn)), for sorting and topological sort.
  • 🧺 Space complexity: O(mn), for graph and result storage.