problemmediumalgorithmsleetcode-1981leetcode 1981leetcode1981

Minimize the Difference Between Target and Chosen Elements

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given an m x n integer matrix mat and an integer target.

Choose one integer from each row in the matrix such that the absolute difference between target and the sum of the chosen elements is minimized.

Return theminimum absolute difference.

The absolute difference between two numbers a and b is the absolute value of a - b.

Examples

Example 1


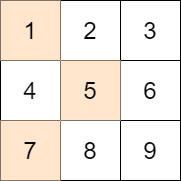
![](https://assets.leetcode.com/uploads/2021/08/03/matrix1.png)

Input: mat = [[1,2,3],[4,5,6],[7,8,9]], target = 13
Output: 0
Explanation: One possible choice is to:
- Choose 1 from the first row.
- Choose 5 from the second row.
- Choose 7 from the third row.
The sum of the chosen elements is 13, which equals the target, so the absolute difference is 0.

Example 2


![](https://assets.leetcode.com/uploads/2021/08/03/matrix1-1.png)

Input: mat = [[1],[2],[3]], target = 100
Output: 94
Explanation: The best possible choice is to:
- Choose 1 from the first row.
- Choose 2 from the second row.
- Choose 3 from the third row.
The sum of the chosen elements is 6, and the absolute difference is 94.

Example 3


![](https://assets.leetcode.com/uploads/2021/08/03/matrix1-3.png)

Input: mat = [[1,2,9,8,7]], target = 6
Output: 1
Explanation: The best choice is to choose 7 from the first row.
The absolute difference is 1.

Constraints

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 70
  • 1 <= mat[i][j] <= 70
  • 1 <= target <= 800

Solution

Method 1 – Dynamic Programming with Bitset

Intuition

We need to pick one element from each row so that the sum is as close as possible to the target. By tracking all possible sums we can form by picking one element per row, we can efficiently find the minimum absolute difference to the target.

Approach

  1. Use a set or bitset to keep track of all possible sums after each row.
  2. For each row, for each possible sum so far, add each element in the row to form new possible sums.
  3. After processing all rows, find the sum with the minimum absolute difference to the target.
  4. Use pruning to avoid unnecessary large sums (e.g., limit to target + max possible row sum).

Code

C++
class Solution {
public:
    int minimizeTheDifference(vector<vector<int>>& mat, int target) {
        int m = mat.size(), n = mat[0].size();
        bitset<5001> dp;
        dp[0] = 1;
        for (int i = 0; i < m; ++i) {
            bitset<5001> ndp;
            for (int s = 0; s <= 5000; ++s) {
                if (dp[s]) {
                    for (int x : mat[i]) {
                        if (s + x <= 5000) ndp[s + x] = 1;
                    }
                }
            }
            dp = ndp;
        }
        int ans = INT_MAX;
        for (int s = 0; s <= 5000; ++s) {
            if (dp[s]) ans = min(ans, abs(s - target));
        }
        return ans;
    }
};
Go
func minimizeTheDifference(mat [][]int, target int) int {
    m, n := len(mat), len(mat[0])
    dp := map[int]struct{}{0: {}}
    for i := 0; i < m; i++ {
        ndp := map[int]struct{}{}
        for s := range dp {
            for _, x := range mat[i] {
                ndp[s+x] = struct{}{}
            }
        }
        dp = ndp
    }
    ans := 1 << 30
    for s := range dp {
        if abs(s-target) < ans {
            ans = abs(s - target)
        }
    }
    return ans
}
func abs(x int) int { if x < 0 { return -x }; return x }
Java
class Solution {
    public int minimizeTheDifference(int[][] mat, int target) {
        Set<Integer> dp = new HashSet<>();
        dp.add(0);
        for (int[] row : mat) {
            Set<Integer> ndp = new HashSet<>();
            for (int s : dp) {
                for (int x : row) ndp.add(s + x);
            }
            dp = ndp;
        }
        int ans = Integer.MAX_VALUE;
        for (int s : dp) ans = Math.min(ans, Math.abs(s - target));
        return ans;
    }
}
Kotlin
class Solution {
    fun minimizeTheDifference(mat: Array<IntArray>, target: Int): Int {
        var dp = setOf(0)
        for (row in mat) {
            val ndp = mutableSetOf<Int>()
            for (s in dp) for (x in row) ndp.add(s + x)
            dp = ndp
        }
        return dp.minOf { kotlin.math.abs(it - target) }
    }
}
Python
def minimize_the_difference(mat: list[list[int]], target: int) -> int:
    dp: set[int] = {0}
    for row in mat:
        ndp = set()
        for s in dp:
            for x in row:
                ndp.add(s + x)
        dp = ndp
    return min(abs(s - target) for s in dp)
Rust
impl Solution {
    pub fn minimize_the_difference(mat: Vec<Vec<i32>>, target: i32) -> i32 {
        let mut dp = std::collections::HashSet::new();
        dp.insert(0);
        for row in mat.iter() {
            let mut ndp = std::collections::HashSet::new();
            for &s in dp.iter() {
                for &x in row.iter() {
                    ndp.insert(s + x);
                }
            }
            dp = ndp;
        }
        dp.into_iter().map(|s| (s - target).abs()).min().unwrap()
    }
}
TypeScript
class Solution {
    minimizeTheDifference(mat: number[][], target: number): number {
        let dp = new Set<number>([0]);
        for (const row of mat) {
            const ndp = new Set<number>();
            for (const s of dp) for (const x of row) ndp.add(s + x);
            dp = ndp;
        }
        let ans = Number.MAX_SAFE_INTEGER;
        for (const s of dp) ans = Math.min(ans, Math.abs(s - target));
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(m * n * S)
    • Where S is the number of possible sums (pruned by constraints, typically up to 5000).
  • 🧺 Space complexity: O(S)
    • For storing possible sums.

Comments