Minimize the Maximum Edge Weight of Graph

Problem

You are given two integers, n and threshold, as well as a directed weighted graph of n nodes numbered from 0 to n - 1. The graph is represented by a 2D integer array edges, where edges[i] = [Ai, Bi, Wi] indicates that there is an edge going from node Ai to node Bi with weight Wi.

You have to remove some edges from this graph (possibly none), so that it satisfies the following conditions:

Node 0 must be reachable from all other nodes.
The maximum edge weight in the resulting graph is minimized.
Each node has at most threshold outgoing edges.

Return the minimum possible value of the maximum edge weight after removing the necessary edges. If it is impossible for all conditions to be satisfied, return -1.

Example 1

1
2
3
4
5
6


Input: n = 5, edges = [[1,0,1],[2,0,2],[3,0,1],[4,3,1],[2,1,1]], threshold
= 2
Output: 1
Explanation:
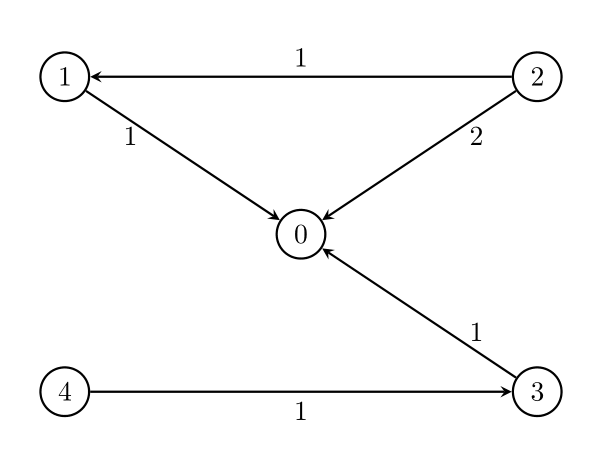
![](https://assets.leetcode.com/uploads/2024/12/09/s-1.png)
Remove the edge `2 -> 0`. The maximum weight among the remaining edges is 1.

Example 2

1
2
3
4
5


Input: n = 5, edges = [[0,1,1],[0,2,2],[0,3,1],[0,4,1],[1,2,1],[1,4,1]],
threshold = 1
Output: -1
Explanation:  
It is impossible to reach node 0 from node 2.

Example 3

1
2
3
4
5
6
7


Input: n = 5, edges = [[1,2,1],[1,3,3],[1,4,5],[2,3,2],[3,4,2],[4,0,1]],
threshold = 1
Output: 2
Explanation:  
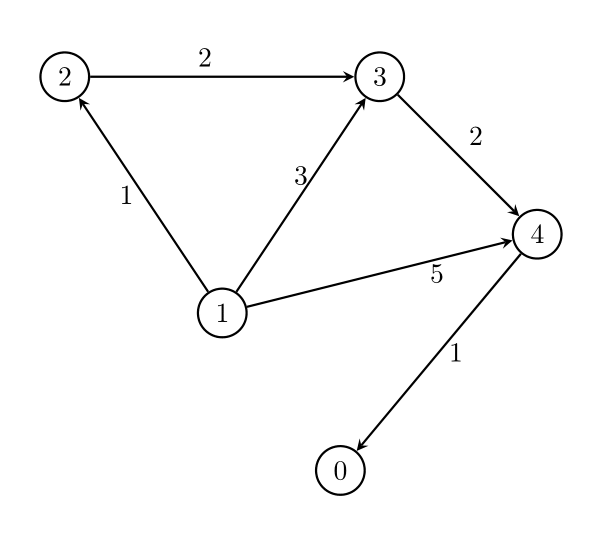
![](https://assets.leetcode.com/uploads/2024/12/09/s2-1.png)
Remove the edges `1 -> 3` and `1 -> 4`. The maximum weight among the remaining
edges is 2.

Example 4

1
2
3


Input: n = 5, edges = [[1,2,1],[1,3,3],[1,4,5],[2,3,2],[4,0,1]], threshold
= 1
Output: -1

Constraints

2 <= n <= 10^5
1 <= threshold <= n - 1
1 <= edges.length <= min(105, n * (n - 1) / 2).
edges[i].length == 3
0 <= Ai, Bi < n
Ai != Bi
1 <= Wi <= 10^6
There may be multiple edges between a pair of nodes, but they must have unique weights.

Examples

Solution

Method 1 – Binary Search + BFS

Intuition

To minimize the maximum edge weight, we can use binary search on the possible edge weights. For each candidate maximum weight, we check if it’s possible to keep only edges with weight ≤ candidate, prune outgoing edges to threshold per node, and ensure node 0 is reachable from all other nodes.

Approach

Use binary search on the maximum edge weight from 1 to the largest edge weight.
For each candidate, build a graph keeping only edges with weight ≤ candidate.
For each node, keep only the threshold smallest outgoing edges.
Use BFS or DFS to check if node 0 is reachable from all other nodes (reverse graph).
If possible, update answer and try lower candidate; else, try higher.
If not possible for any candidate, return -1.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


class Solution {
public:
    int minimizeMaxEdgeWeight(int n, vector<vector<int>>& edges, int threshold) {
        int lo = 1, hi = 0;
        for (auto& e : edges) hi = max(hi, e[2]);
        int ans = -1;
        while (lo <= hi) {
            int mid = lo + (hi - lo) / 2;
            vector<vector<pair<int,int>>> g(n);
            for (auto& e : edges) {
                if (e[2] <= mid) g[e[0]].emplace_back(e[1], e[2]);
            }
            for (int i = 0; i < n; ++i) {
                sort(g[i].begin(), g[i].end(), [](auto& a, auto& b){ return a.second < b.second; });
                if (g[i].size() > threshold) g[i].resize(threshold);
            }
            vector<bool> vis(n);
            queue<int> q;
            q.push(0); vis[0] = true;
            while (!q.empty()) {
                int u = q.front(); q.pop();
                for (auto& [v, w] : g[u]) {
                    if (!vis[v]) { vis[v] = true; q.push(v); }
                }
            }
            bool ok = true;
            for (int i = 0; i < n; ++i) if (!vis[i]) ok = false;
            if (ok) { ans = mid; hi = mid - 1; }
            else lo = mid + 1;
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47


func minimizeMaxEdgeWeight(n int, edges [][]int, threshold int) int {
    lo, hi := 1, 0
    for _, e := range edges {
        if e[2] > hi { hi = e[2] }
    }
    ans := -1
    for lo <= hi {
        mid := lo + (hi-lo)/2
        g := make([][][2]int, n)
        for _, e := range edges {
            if e[2] <= mid {
                g[e[0]] = append(g[e[0]], [2]int{e[1], e[2]})
            }
        }
        for i := 0; i < n; i++ {
            sort.Slice(g[i], func(a, b int) bool { return g[i][a][1] < g[i][b][1] })
            if len(g[i]) > threshold {
                g[i] = g[i][:threshold]
            }
        }
        vis := make([]bool, n)
        q := []int{0}
        vis[0] = true
        for len(q) > 0 {
            u := q[0]
            q = q[1:]
            for _, vw := range g[u] {
                v := vw[0]
                if !vis[v] {
                    vis[v] = true
                    q = append(q, v)
                }
            }
        }
        ok := true
        for i := 0; i < n; i++ {
            if !vis[i] { ok = false }
        }
        if ok {
            ans = mid
            hi = mid - 1
        } else {
            lo = mid + 1
        }
    }
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


class Solution {
    public int minimizeMaxEdgeWeight(int n, int[][] edges, int threshold) {
        int lo = 1, hi = 0;
        for (int[] e : edges) hi = Math.max(hi, e[2]);
        int ans = -1;
        while (lo <= hi) {
            int mid = lo + (hi - lo) / 2;
            List<List<int[]>> g = new ArrayList<>();
            for (int i = 0; i < n; ++i) g.add(new ArrayList<>());
            for (int[] e : edges) {
                if (e[2] <= mid) g.get(e[0]).add(new int[]{e[1], e[2]});
            }
            for (int i = 0; i < n; ++i) {
                g.get(i).sort(Comparator.comparingInt(a -> a[1]));
                if (g.get(i).size() > threshold) g.get(i).subList(threshold, g.get(i).size()).clear();
            }
            boolean[] vis = new boolean[n];
            Queue<Integer> q = new LinkedList<>();
            q.add(0); vis[0] = true;
            while (!q.isEmpty()) {
                int u = q.poll();
                for (int[] vw : g.get(u)) {
                    int v = vw[0];
                    if (!vis[v]) { vis[v] = true; q.add(v); }
                }
            }
            boolean ok = true;
            for (int i = 0; i < n; ++i) if (!vis[i]) ok = false;
            if (ok) { ans = mid; hi = mid - 1; }
            else lo = mid + 1;
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


class Solution {
    fun minimizeMaxEdgeWeight(n: Int, edges: Array<IntArray>, threshold: Int): Int {
        var lo = 1
        var hi = edges.maxOf { it[2] }
        var ans = -1
        while (lo <= hi) {
            val mid = lo + (hi-lo)/2
            val g = Array(n) { mutableListOf<Pair<Int,Int>>() }
            for (e in edges) if (e[2] <= mid) g[e[0]].add(e[1] to e[2])
            for (i in 0 until n) {
                g[i].sortBy { it.second }
                if (g[i].size > threshold) g[i] = g[i].take(threshold).toMutableList()
            }
            val vis = BooleanArray(n)
            val q = ArrayDeque<Int>()
            q.add(0); vis[0] = true
            while (q.isNotEmpty()) {
                val u = q.removeFirst()
                for ((v, _) in g[u]) {
                    if (!vis[v]) { vis[v] = true; q.add(v) }
                }
            }
            val ok = vis.all { it }
            if (ok) { ans = mid; hi = mid-1 }
            else lo = mid+1
        }
        return ans
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


def minimize_max_edge_weight(n: int, edges: list[list[int]], threshold: int) -> int:
    lo, hi = 1, max(w for _,_,w in edges)
    ans = -1
    while lo <= hi:
        mid = (lo + hi) // 2
        g = [[] for _ in range(n)]
        for a, b, w in edges:
            if w <= mid:
                g[a].append((b, w))
        for i in range(n):
            g[i].sort(key=lambda x: x[1])
            if len(g[i]) > threshold:
                g[i] = g[i][:threshold]
        vis = [False]*n
        q = [0]
        vis[0] = True
        while q:
            u = q.pop(0)
            for v, _ in g[u]:
                if not vis[v]:
                    vis[v] = True
                    q.append(v)
        if all(vis):
            ans = mid
            hi = mid - 1
        else:
            lo = mid + 1
    return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38


impl Solution {
    pub fn minimize_max_edge_weight(n: i32, edges: Vec<Vec<i32>>, threshold: i32) -> i32 {
        let n = n as usize;
        let mut lo = 1;
        let mut hi = edges.iter().map(|e| e[2]).max().unwrap();
        let mut ans = -1;
        while lo <= hi {
            let mid = lo + (hi-lo)/2;
            let mut g = vec![vec![]; n];
            for e in edges.iter() {
                if e[2] <= mid {
                    g[e[0] as usize].push((e[1] as usize, e[2]));
                }
            }
            for i in 0..n {
                g[i].sort_by_key(|x| x.1);
                if g[i].len() > threshold as usize {
                    g[i].truncate(threshold as usize);
                }
            }
            let mut vis = vec![false; n];
            let mut q = std::collections::VecDeque::new();
            q.push_back(0); vis[0] = true;
            while let Some(u) = q.pop_front() {
                for &(v, _) in &g[u] {
                    if !vis[v] { vis[v] = true; q.push_back(v); }
                }
            }
            if vis.iter().all(|&x| x) {
                ans = mid;
                hi = mid-1;
            } else {
                lo = mid+1;
            }
        }
        ans
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


class Solution {
    minimizeMaxEdgeWeight(n: number, edges: number[][], threshold: number): number {
        let lo = 1, hi = Math.max(...edges.map(e => e[2]));
        let ans = -1;
        while (lo <= hi) {
            const mid = Math.floor((lo + hi) / 2);
            const g: [number, number][][] = Array.from({length: n}, () => []);
            for (const [a, b, w] of edges) {
                if (w <= mid) g[a].push([b, w]);
            }
            for (let i = 0; i < n; ++i) {
                g[i].sort((a, b) => a[1] - b[1]);
                if (g[i].length > threshold) g[i] = g[i].slice(0, threshold);
            }
            const vis = Array(n).fill(false);
            const q = [0];
            vis[0] = true;
            while (q.length) {
                const u = q.shift()!;
                for (const [v, _] of g[u]) {
                    if (!vis[v]) { vis[v] = true; q.push(v); }
                }
            }
            if (vis.every(x => x)) {
                ans = mid;
                hi = mid - 1;
            } else {
                lo = mid + 1;
            }
        }
        return ans;
    }
}

Complexity

⏰ Time complexity: O(E log W + N log N)
- E = number of edges, W = max edge weight, N = number of nodes. Sorting outgoing edges per node and BFS per candidate.
🧺 Space complexity: O(E + N)
- For graph and visited array.

Problem#

Example 1#

Example 2#

Example 3#

Example 4#

Constraints#

Examples#

Solution#

Method 1 – Binary Search + BFS#

Intuition#

Approach#

Code#

Complexity#