Problem

There exists an undirected and unrooted tree with n nodes indexed from 0 to n - 1. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

Each node has an associated price. You are given an integer array price, where price[i] is the price of the ith node.

The price sum of a given path is the sum of the prices of all nodes lying on that path.

Additionally, you are given a 2D integer array trips, where trips[i] = [starti, endi] indicates that you start the ith trip from the node starti and travel to the node endi by any path you like.

Before performing your first trip, you can choose some non-adjacent nodes and halve the prices.

Return the minimum total price sum to perform all the given trips.

Examples

Example 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


![](https://assets.leetcode.com/uploads/2023/03/16/diagram2.png)

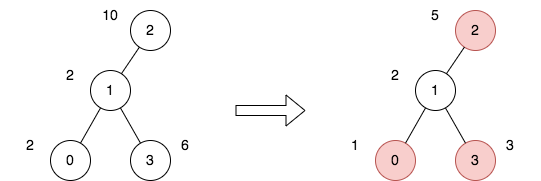
Input: n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]
Output: 23
Explanation: The diagram above denotes the tree after rooting it at node 2. The first part shows the initial tree and the second part shows the tree after choosing nodes 0, 2, and 3, and making their price half.
For the 1st trip, we choose path [0,1,3]. The price sum of that path is 1 + 2 + 3 = 6.
For the 2nd trip, we choose path [2,1]. The price sum of that path is 2 + 5 = 7.
For the 3rd trip, we choose path [2,1,3]. The price sum of that path is 5 + 2 + 3 = 10.
The total price sum of all trips is 6 + 7 + 10 = 23.
It can be proven, that 23 is the minimum answer that we can achieve.

Example 2

1
2
3
4
5
6
7
8


![](https://assets.leetcode.com/uploads/2023/03/16/diagram3.png)

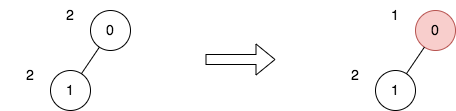
Input: n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]]
Output: 1
Explanation: The diagram above denotes the tree after rooting it at node 0. The first part shows the initial tree and the second part shows the tree after choosing node 0, and making its price half.
For the 1st trip, we choose path [0]. The price sum of that path is 1.
The total price sum of all trips is 1. It can be proven, that 1 is the minimum answer that we can achieve.

Constraints

  • 1 <= n <= 50
  • edges.length == n - 1
  • 0 <= ai, bi <= n - 1
  • edges represents a valid tree.
  • price.length == n
  • price[i] is an even integer.
  • 1 <= price[i] <= 1000
  • 1 <= trips.length <= 100
  • 0 <= starti, endi <= n - 1

Solution

Method 1 – Tree DP (Dynamic Programming on Trees)

Intuition

Each trip increases the usage count of nodes along its path. To minimize the total price, we can halve the price of some nodes (but not adjacent ones). This is a classic tree DP problem: for each node, decide whether to halve its price or not, ensuring no two adjacent nodes are halved.

Approach

  1. Build the tree from edges.
  2. For each trip, increment the usage count for all nodes along the path (use DFS to find paths).
  3. Use DP on the tree:
    • For each node, compute two values:
      • Cost if this node is halved (children cannot be halved).
      • Cost if this node is not halved (children can be halved or not).
  4. The answer is the minimum of the two values at the root.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class Solution {
public:
    int minimizeTotalPrice(int n, vector<vector<int>>& edges, vector<int>& price, vector<vector<int>>& trips) {
        vector<vector<int>> g(n);
        for (auto& e : edges) {
            g[e[0]].push_back(e[1]);
            g[e[1]].push_back(e[0]);
        }
        vector<int> cnt(n);
        function<bool(int,int,int)> dfs = [&](int u, int v, int p) {
            if (u == v) { cnt[u]++; return true; }
            for (int x : g[u]) if (x != p && dfs(x, v, u)) { cnt[u]++; return true; }
            return false;
        };
        for (auto& t : trips) dfs(t[0], t[1], -1);
        function<pair<long,long>(int,int)> dp = [&](int u, int p) {
            long half = cnt[u] * price[u] / 2, full = cnt[u] * price[u];
            for (int x : g[u]) if (x != p) {
                auto [h, f] = dp(x, u);
                half += f;
                full += min(h, f);
            }
            return make_pair(half, full);
        };
        auto [h, f] = dp(0, -1);
        return min(h, f);
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

func minimizeTotalPrice(n int, edges [][]int, price []int, trips [][]int) int {
    g := make([][]int, n)
    for _, e := range edges {
        g[e[0]] = append(g[e[0]], e[1])
        g[e[1]] = append(g[e[1]], e[0])
    }
    cnt := make([]int, n)
    var dfs func(u, v, p int) bool
    dfs = func(u, v, p int) bool {
        if u == v { cnt[u]++; return true }
        for _, x := range g[u] {
            if x != p && dfs(x, v, u) { cnt[u]++; return true }
        }
        return false
    }
    for _, t := range trips { dfs(t[0], t[1], -1) }
    var dp func(u, p int) (int, int)
    dp = func(u, p int) (int, int) {
        half := cnt[u] * price[u] / 2
        full := cnt[u] * price[u]
        for _, x := range g[u] {
            if x != p {
                h, f := dp(x, u)
                half += f
                full += min(h, f)
            }
        }
        return half, full
    }
    h, f := dp(0, -1)
    return min(h, f)
}
func min(a, b int) int { if a < b { return a } else { return b } }
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class Solution {
    public int minimizeTotalPrice(int n, int[][] edges, int[] price, int[][] trips) {
        List<List<Integer>> g = new ArrayList<>();
        for (int i = 0; i < n; ++i) g.add(new ArrayList<>());
        for (int[] e : edges) {
            g.get(e[0]).add(e[1]);
            g.get(e[1]).add(e[0]);
        }
        int[] cnt = new int[n];
        for (int[] t : trips) dfs(g, cnt, t[0], t[1], -1);
        int[] res = dp(g, cnt, price, 0, -1);
        return Math.min(res[0], res[1]);
    }
    private boolean dfs(List<List<Integer>> g, int[] cnt, int u, int v, int p) {
        if (u == v) { cnt[u]++; return true; }
        for (int x : g.get(u)) if (x != p && dfs(g, cnt, x, v, u)) { cnt[u]++; return true; }
        return false;
    }
    private int[] dp(List<List<Integer>> g, int[] cnt, int[] price, int u, int p) {
        int half = cnt[u] * price[u] / 2, full = cnt[u] * price[u];
        for (int x : g.get(u)) if (x != p) {
            int[] r = dp(g, cnt, price, x, u);
            half += r[1];
            full += Math.min(r[0], r[1]);
        }
        return new int[]{half, full};
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class Solution {
    fun minimizeTotalPrice(n: Int, edges: Array<IntArray>, price: IntArray, trips: Array<IntArray>): Int {
        val g = Array(n) { mutableListOf<Int>() }
        for (e in edges) {
            g[e[0]].add(e[1])
            g[e[1]].add(e[0])
        }
        val cnt = IntArray(n)
        fun dfs(u: Int, v: Int, p: Int): Boolean {
            if (u == v) { cnt[u]++; return true }
            for (x in g[u]) if (x != p && dfs(x, v, u)) { cnt[u]++; return true }
            return false
        }
        for (t in trips) dfs(t[0], t[1], -1)
        fun dp(u: Int, p: Int): Pair<Int, Int> {
            var half = cnt[u] * price[u] / 2
            var full = cnt[u] * price[u]
            for (x in g[u]) if (x != p) {
                val (h, f) = dp(x, u)
                half += f
                full += minOf(h, f)
            }
            return half to full
        }
        val (h, f) = dp(0, -1)
        return minOf(h, f)
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

def minimize_total_price(n: int, edges: list[list[int]], price: list[int], trips: list[list[int]]) -> int:
    from collections import defaultdict
    g = defaultdict(list)
    for a, b in edges:
        g[a].append(b)
        g[b].append(a)
    cnt = [0] * n
    def dfs(u: int, v: int, p: int) -> bool:
        if u == v:
            cnt[u] += 1
            return True
        for x in g[u]:
            if x != p and dfs(x, v, u):
                cnt[u] += 1
                return True
        return False
    for s, e in trips:
        dfs(s, e, -1)
    def dp(u: int, p: int) -> tuple[int, int]:
        half = cnt[u] * price[u] // 2
        full = cnt[u] * price[u]
        for x in g[u]:
            if x != p:
                h, f = dp(x, u)
                half += f
                full += min(h, f)
        return half, full
    h, f = dp(0, -1)
    return min(h, f)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

impl Solution {
    pub fn minimize_total_price(n: i32, edges: Vec<Vec<i32>>, price: Vec<i32>, trips: Vec<Vec<i32>>) -> i32 {
        use std::collections::HashMap;
        let n = n as usize;
        let mut g = vec![vec![]; n];
        for e in edges.iter() {
            g[e[0] as usize].push(e[1] as usize);
            g[e[1] as usize].push(e[0] as usize);
        }
        let mut cnt = vec![0; n];
        fn dfs(g: &Vec<Vec<usize>>, cnt: &mut Vec<i32>, u: usize, v: usize, p: isize) -> bool {
            if u == v { cnt[u] += 1; return true; }
            for &x in &g[u] {
                if x != p as usize && dfs(g, cnt, x, v, u as isize) {
                    cnt[u] += 1;
                    return true;
                }
            }
            false
        }
        for t in trips.iter() {
            dfs(&g, &mut cnt, t[0] as usize, t[1] as usize, -1);
        }
        fn dp(g: &Vec<Vec<usize>>, cnt: &Vec<i32>, price: &Vec<i32>, u: usize, p: isize) -> (i32, i32) {
            let mut half = cnt[u] * price[u] / 2;
            let mut full = cnt[u] * price[u];
            for &x in &g[u] {
                if x != p as usize {
                    let (h, f) = dp(g, cnt, price, x, u as isize);
                    half += f;
                    full += h.min(f);
                }
            }
            (half, full)
        }
        let (h, f) = dp(&g, &cnt, &price, 0, -1);
        h.min(f)
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class Solution {
    minimizeTotalPrice(n: number, edges: number[][], price: number[], trips: number[][]): number {
        const g: number[][][] = Array.from({length: n}, () => []);
        for (const [a, b] of edges) {
            g[a].push(b);
            g[b].push(a);
        }
        const cnt = Array(n).fill(0);
        function dfs(u: number, v: number, p: number): boolean {
            if (u === v) { cnt[u]++; return true; }
            for (const x of g[u]) if (x !== p && dfs(x, v, u)) { cnt[u]++; return true; }
            return false;
        }
        for (const [s, e] of trips) dfs(s, e, -1);
        function dp(u: number, p: number): [number, number] {
            let half = Math.floor(cnt[u] * price[u] / 2);
            let full = cnt[u] * price[u];
            for (const x of g[u]) if (x !== p) {
                const [h, f] = dp(x, u);
                half += f;
                full += Math.min(h, f);
            }
            return [half, full];
        }
        const [h, f] = dp(0, -1);
        return Math.min(h, f);
    }
}

Complexity

  • ⏰ Time complexity: O(n^2)
    • Each trip may traverse the tree, and DP is O(n).
  • 🧺 Space complexity: O(n)
    • For tree, count, and DP stack.