Minimum Array Length After Pair Removals

Problem

Given an integer array num sorted in non-decreasing order.

You can perform the following operation any number of times:

• Choose two indices, i and j, where nums[i] < nums[j].
• Then, remove the elements at indices i and j from nums. The remaining elements retain their original order, and the array is re-indexed.

Return the minimum length of nums after applying the operation zero or more times.

Examples

Example 1

Input: nums = [1,2,3,4]

Output: 0

Explanation:

![](https://assets.leetcode.com/uploads/2024/05/18/tcase1.gif)

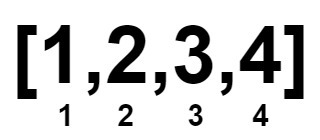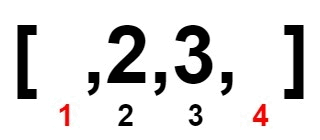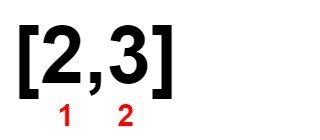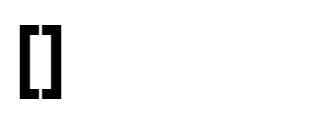
Example 2

Input: nums = [1,1,2,2,3,3]

Output: 0

Explanation:

![](https://assets.leetcode.com/uploads/2024/05/19/tcase2.gif)

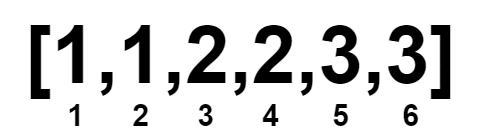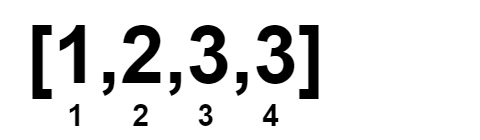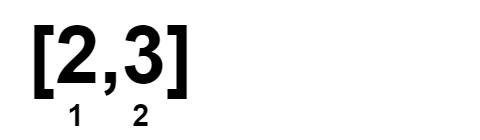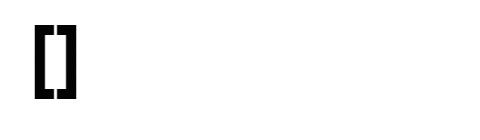
Example 3

Input: nums = [1000000000,1000000000]

Output: 2

Explanation:

Since both numbers are equal, they cannot be removed.

#### Example 4

Input: nums = [2,3,4,4,4]

Output: 1

Explanation:

![](https://assets.leetcode.com/uploads/2024/05/19/tcase3.gif)

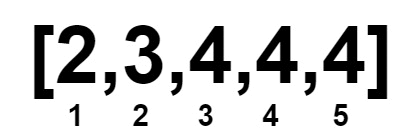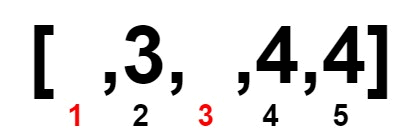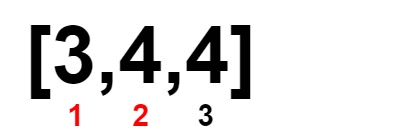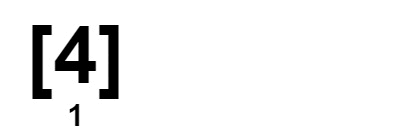
Constraints

• 1 <= nums.length <= 10^5
• 1 <= nums[i] <= 10^9
• nums is sorted in non-decreasing order.

Solution

Method 1 – Two Pointers + Greedy

Intuition

To minimize the array length, we want to remove as many pairs as possible where nums[i] < nums[j]. Since the array is sorted, we can use two pointers: one starting from the left and one from the right, and greedily pair the smallest with the largest possible.

Approach

1. Initialize two pointers: left at 0, right at n-1.
2. While left < right:
   • If nums[left] < nums[right], remove both and move left++, right--.
   • Else, move right-- (since nums[left] >= nums[right], try next largest).
3. Count the number of pairs removed.
4. The minimum length is n - 2 * pairs.

Code

C++

class Solution {
public:
    int minLengthAfterRemovals(vector<int>& nums) {
        int n = nums.size(), left = 0, right = n-1, pairs = 0;
        while (left < right) {
            if (nums[left] < nums[right]) {
                pairs++;
                left++;
                right--;
            } else {
                right--;
            }
        }
        return n - 2 * pairs;
    }
};

Go

func minLengthAfterRemovals(nums []int) int {
    n, left, right, pairs := len(nums), 0, len(nums)-1, 0
    for left < right {
        if nums[left] < nums[right] {
            pairs++
            left++
            right--
        } else {
            right--
        }
    }
    return n - 2*pairs
}

Java

class Solution {
    public int minLengthAfterRemovals(int[] nums) {
        int n = nums.length, left = 0, right = n-1, pairs = 0;
        while (left < right) {
            if (nums[left] < nums[right]) {
                pairs++;
                left++;
                right--;
            } else {
                right--;
            }
        }
        return n - 2 * pairs;
    }
}

Kotlin

class Solution {
    fun minLengthAfterRemovals(nums: IntArray): Int {
        var left = 0
        var right = nums.size - 1
        var pairs = 0
        while (left < right) {
            if (nums[left] < nums[right]) {
                pairs++
                left++
                right--
            } else {
                right--
            }
        }
        return nums.size - 2 * pairs
    }
}

Python

def min_length_after_removals(nums: list[int]) -> int:
    n = len(nums)
    left, right = 0, n-1
    pairs = 0
    while left < right:
        if nums[left] < nums[right]:
            pairs += 1
            left += 1
            right -= 1
        else:
            right -= 1
    return n - 2 * pairs

Rust

impl Solution {
    pub fn min_length_after_removals(nums: Vec<i32>) -> i32 {
        let n = nums.len();
        let (mut left, mut right, mut pairs) = (0, n-1, 0);
        while left < right {
            if nums[left] < nums[right] {
                pairs += 1;
                left += 1;
                right -= 1;
            } else {
                right -= 1;
            }
        }
        (n - 2 * pairs) as i32
    }
}

TypeScript

class Solution {
    minLengthAfterRemovals(nums: number[]): number {
        let left = 0, right = nums.length - 1, pairs = 0;
        while (left < right) {
            if (nums[left] < nums[right]) {
                pairs++;
                left++;
                right--;
            } else {
                right--;
            }
        }
        return nums.length - 2 * pairs;
    }
}

Complexity

• ⏰ Time complexity: O(n)
  • Each element is processed at most once.
• 🧺 Space complexity: O(1)
  • Only a few variables used.