Minimum Cost for Cutting Cake II

Problem

There is an m x n cake that needs to be cut into 1 x 1 pieces.

You are given integers m, n, and two arrays:

• horizontalCut of size m - 1, where horizontalCut[i] represents the cost to cut along the horizontal line i.
• verticalCut of size n - 1, where verticalCut[j] represents the cost to cut along the vertical line j.

In one operation, you can choose any piece of cake that is not yet a 1 x 1 square and perform one of the following cuts:

1. Cut along a horizontal line i at a cost of horizontalCut[i].
2. Cut along a vertical line j at a cost of verticalCut[j].

After the cut, the piece of cake is divided into two distinct pieces.

The cost of a cut depends only on the initial cost of the line and does not change.

Return the minimum total cost to cut the entire cake into 1 x 1 pieces.

Examples

Example 1

Input: m = 3, n = 2, horizontalCut = [1,3], verticalCut = [5]

Output: 13

Explanation:

![](https://assets.leetcode.com/uploads/2024/06/04/ezgifcom-animated-gif-
maker-1.gif)

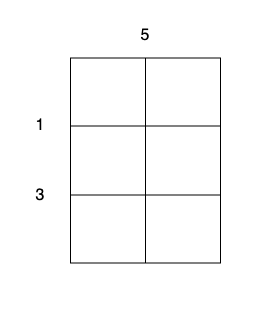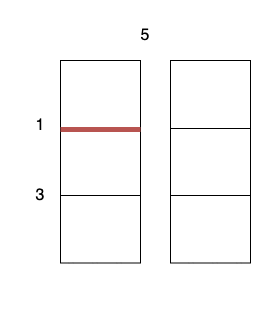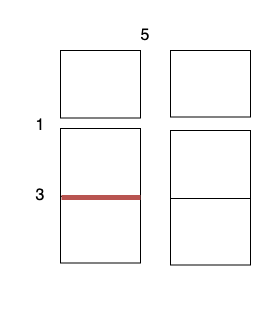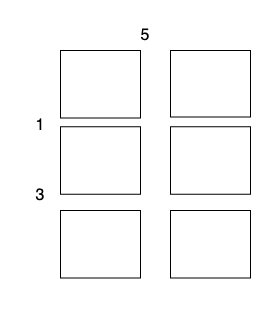
  * Perform a cut on the vertical line 0 with cost 5, current total cost is 5.
  * Perform a cut on the horizontal line 0 on `3 x 1` subgrid with cost 1.
  * Perform a cut on the horizontal line 0 on `3 x 1` subgrid with cost 1.
  * Perform a cut on the horizontal line 1 on `2 x 1` subgrid with cost 3.
  * Perform a cut on the horizontal line 1 on `2 x 1` subgrid with cost 3.

The total cost is `5 + 1 + 1 + 3 + 3 = 13`.

Example 2

Input: m = 2, n = 2, horizontalCut = [7], verticalCut = [4]

Output: 15

Explanation:

  * Perform a cut on the horizontal line 0 with cost 7.
  * Perform a cut on the vertical line 0 on `1 x 2` subgrid with cost 4.
  * Perform a cut on the vertical line 0 on `1 x 2` subgrid with cost 4.

The total cost is `7 + 4 + 4 = 15`.

Constraints

• 1 <= m, n <= 10^5
• horizontalCut.length == m - 1
• verticalCut.length == n - 1
• 1 <= horizontalCut[i], verticalCut[i] <= 10^3

Solution

Method 1 – Greedy: Sort and Cut Highest Cost First

Intuition

To minimize the total cost, always cut the highest cost line available. Each cut increases the number of pieces in the other direction, so prioritize the most expensive cuts to maximize their multiplication effect.

Approach

1. Sort both horizontalCut and verticalCut in descending order.
2. Use two pointers to process cuts:
   • At each step, pick the higher cost cut (horizontal or vertical).
   • Multiply the cost by the current number of pieces in the other direction.
   • Update the number of pieces accordingly.
3. Continue until all cuts are processed.
4. Return the total cost.

Code

C++

class Solution {
public:
    int minCost(vector<int>& horizontalCut, vector<int>& verticalCut) {
        sort(horizontalCut.rbegin(), horizontalCut.rend());
        sort(verticalCut.rbegin(), verticalCut.rend());
        int h = 1, v = 1, i = 0, j = 0, ans = 0;
        while (i < horizontalCut.size() && j < verticalCut.size()) {
            if (horizontalCut[i] >= verticalCut[j]) {
                ans += horizontalCut[i] * v;
                h++;
                i++;
            } else {
                ans += verticalCut[j] * h;
                v++;
                j++;
            }
        }
        while (i < horizontalCut.size()) {
            ans += horizontalCut[i] * v;
            i++;
        }
        while (j < verticalCut.size()) {
            ans += verticalCut[j] * h;
            j++;
        }
        return ans;
    }
};

Go

func minCost(horizontalCut, verticalCut []int) int {
    sort.Slice(horizontalCut, func(i, j int) bool { return horizontalCut[i] > horizontalCut[j] })
    sort.Slice(verticalCut, func(i, j int) bool { return verticalCut[i] > verticalCut[j] })
    h, v := 1, 1
    i, j, ans := 0, 0, 0
    for i < len(horizontalCut) && j < len(verticalCut) {
        if horizontalCut[i] >= verticalCut[j] {
            ans += horizontalCut[i] * v
            h++
            i++
        } else {
            ans += verticalCut[j] * h
            v++
            j++
        }
    }
    for i < len(horizontalCut) {
        ans += horizontalCut[i] * v
        i++
    }
    for j < len(verticalCut) {
        ans += verticalCut[j] * h
        j++
    }
    return ans
}

Java

class Solution {
    public int minCost(int[] horizontalCut, int[] verticalCut) {
        Arrays.sort(horizontalCut);
        Arrays.sort(verticalCut);
        int h = 1, v = 1, i = horizontalCut.length - 1, j = verticalCut.length - 1, ans = 0;
        while (i >= 0 && j >= 0) {
            if (horizontalCut[i] >= verticalCut[j]) {
                ans += horizontalCut[i] * v;
                h++;
                i--;
            } else {
                ans += verticalCut[j] * h;
                v++;
                j--;
            }
        }
        while (i >= 0) {
            ans += horizontalCut[i] * v;
            i--;
        }
        while (j >= 0) {
            ans += verticalCut[j] * h;
            j--;
        }
        return ans;
    }
}

Kotlin

class Solution {
    fun minCost(horizontalCut: IntArray, verticalCut: IntArray): Int {
        horizontalCut.sortDescending()
        verticalCut.sortDescending()
        var h = 1
        var v = 1
        var i = 0
        var j = 0
        var ans = 0
        while (i < horizontalCut.size && j < verticalCut.size) {
            if (horizontalCut[i] >= verticalCut[j]) {
                ans += horizontalCut[i] * v
                h++
                i++
            } else {
                ans += verticalCut[j] * h
                v++
                j++
            }
        }
        while (i < horizontalCut.size) {
            ans += horizontalCut[i] * v
            i++
        }
        while (j < verticalCut.size) {
            ans += verticalCut[j] * h
            j++
        }
        return ans
    }
}

Python

def min_cost(horizontal_cut: list[int], vertical_cut: list[int]) -> int:
    horizontal_cut.sort(reverse=True)
    vertical_cut.sort(reverse=True)
    h, v = 1, 1
    i, j = 0, 0
    ans = 0
    while i < len(horizontal_cut) and j < len(vertical_cut):
        if horizontal_cut[i] >= vertical_cut[j]:
            ans += horizontal_cut[i] * v
            h += 1
            i += 1
        else:
            ans += vertical_cut[j] * h
            v += 1
            j += 1
    while i < len(horizontal_cut):
        ans += horizontal_cut[i] * v
        i += 1
    while j < len(vertical_cut):
        ans += vertical_cut[j] * h
        j += 1
    return ans

Rust

impl Solution {
    pub fn min_cost(horizontal_cut: Vec<i32>, vertical_cut: Vec<i32>) -> i32 {
        let mut hcut = horizontal_cut;
        let mut vcut = vertical_cut;
        hcut.sort_by(|a, b| b.cmp(a));
        vcut.sort_by(|a, b| b.cmp(a));
        let (mut h, mut v) = (1, 1);
        let (mut i, mut j) = (0, 0);
        let mut ans = 0;
        while i < hcut.len() && j < vcut.len() {
            if hcut[i] >= vcut[j] {
                ans += hcut[i] * v as i32;
                h += 1;
                i += 1;
            } else {
                ans += vcut[j] * h as i32;
                v += 1;
                j += 1;
            }
        }
        while i < hcut.len() {
            ans += hcut[i] * v as i32;
            i += 1;
        }
        while j < vcut.len() {
            ans += vcut[j] * h as i32;
            j += 1;
        }
        ans
    }
}

TypeScript

class Solution {
    minCost(horizontalCut: number[], verticalCut: number[]): number {
        horizontalCut.sort((a, b) => b - a);
        verticalCut.sort((a, b) => b - a);
        let h = 1, v = 1, i = 0, j = 0, ans = 0;
        while (i < horizontalCut.length && j < verticalCut.length) {
            if (horizontalCut[i] >= verticalCut[j]) {
                ans += horizontalCut[i] * v;
                h++;
                i++;
            } else {
                ans += verticalCut[j] * h;
                v++;
                j++;
            }
        }
        while (i < horizontalCut.length) {
            ans += horizontalCut[i] * v;
            i++;
        }
        while (j < verticalCut.length) {
            ans += verticalCut[j] * h;
            j++;
        }
        return ans;
    }
}

Complexity

• ⏰ Time complexity: O((m + n) log (m + n)), for sorting both cut arrays and iterating through them.
• 🧺 Space complexity: O(1), only a few variables are used for pointers and counters.