Minimum Cost Homecoming of a Robot in a Grid

Problem

There is an m x n grid, where (0, 0) is the top-left cell and (m - 1, n -1) is the bottom-right cell. You are given an integer array startPos where startPos = [startrow, startcol] indicates that initially , a robot is at the cell (startrow, startcol). You are also given an integer array homePos where homePos = [homerow, homecol] indicates that its home is at the cell (homerow, homecol).

The robot needs to go to its home. It can move one cell in four directions: left , right , up , or down , and it can not move outside the boundary. Every move incurs some cost. You are further given two 0-indexed integer arrays: rowCosts of length m and colCosts of length n.

If the robot moves up or down into a cell whose row is r, then this move costs rowCosts[r].
If the robot moves left or right into a cell whose column is c, then this move costs colCosts[c].

Return theminimum total cost for this robot to return home.

Examples

Example 1


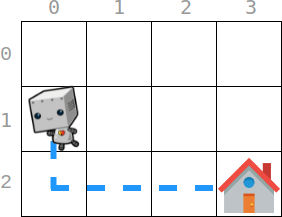
![](https://assets.leetcode.com/uploads/2021/10/11/eg-1.png)

Input: startPos = [1, 0], homePos = [2, 3], rowCosts = [5, 4, 3], colCosts = [8, 2, 6, 7]
Output: 18
Explanation: One optimal path is that:
Starting from (1, 0)
-> It goes down to (_**2**_ , 0). This move costs rowCosts[2] = 3.
-> It goes right to (2, _**1**_). This move costs colCosts[1] = 2.
-> It goes right to (2, _**2**_). This move costs colCosts[2] = 6.
-> It goes right to (2, _**3**_). This move costs colCosts[3] = 7.
The total cost is 3 + 2 + 6 + 7 = 18

Example 2

Input: startPos = [0, 0], homePos = [0, 0], rowCosts = [5], colCosts = [26]
Output: 0
Explanation: The robot is already at its home. Since no moves occur, the total cost is 0.

Constraints

m == rowCosts.length
n == colCosts.length
1 <= m, n <= 10^5
0 <= rowCosts[r], colCosts[c] <= 10^4
startPos.length == 2
homePos.length == 2
0 <= startrow, homerow < m
0 <= startcol, homecol < n

Solution

Method 1 – Greedy Traversal

Intuition

The robot can move independently in rows and columns. The cost for each move is fixed by the destination row or column. So, the minimum cost is simply the sum of costs for all rows and columns traversed from start to home.

Approach

Start from the robot's initial position.
Move towards the home position row by row:
- If startrow < homerow, move down; else if startrow > homerow, move up.
- For each row traversed, add the corresponding row cost.
Move towards the home position column by column:
- If startcol < homecol, move right; else if startcol > homecol, move left.
- For each column traversed, add the corresponding column cost.
Stop when both row and column match the home position.

Code

C++

class Solution {
public:
    int minCost(vector<int>& startPos, vector<int>& homePos, vector<int>& rowCosts, vector<int>& colCosts) {
        int ans = 0;
        int r = startPos[0], c = startPos[1];
        while (r != homePos[0]) {
            r += (homePos[0] > r ? 1 : -1);
            ans += rowCosts[r];
        }
        while (c != homePos[1]) {
            c += (homePos[1] > c ? 1 : -1);
            ans += colCosts[c];
        }
        return ans;
    }
};

Go

func minCost(startPos []int, homePos []int, rowCosts []int, colCosts []int) int {
    ans := 0
    r, c := startPos[0], startPos[1]
    for r != homePos[0] {
        if homePos[0] > r {
            r++
        } else {
            r--
        }
        ans += rowCosts[r]
    }
    for c != homePos[1] {
        if homePos[1] > c {
            c++
        } else {
            c--
        }
        ans += colCosts[c]
    }
    return ans
}

Java

class Solution {
    public int minCost(int[] startPos, int[] homePos, int[] rowCosts, int[] colCosts) {
        int ans = 0, r = startPos[0], c = startPos[1];
        while (r != homePos[0]) {
            r += (homePos[0] > r ? 1 : -1);
            ans += rowCosts[r];
        }
        while (c != homePos[1]) {
            c += (homePos[1] > c ? 1 : -1);
            ans += colCosts[c];
        }
        return ans;
    }
}

Kotlin

class Solution {
    fun minCost(startPos: IntArray, homePos: IntArray, rowCosts: IntArray, colCosts: IntArray): Int {
        var ans = 0
        var r = startPos[0]
        var c = startPos[1]
        while (r != homePos[0]) {
            r += if (homePos[0] > r) 1 else -1
            ans += rowCosts[r]
        }
        while (c != homePos[1]) {
            c += if (homePos[1] > c) 1 else -1
            ans += colCosts[c]
        }
        return ans
    }
}

Python

def minCost(startPos: list[int], homePos: list[int], rowCosts: list[int], colCosts: list[int]) -> int:
    ans = 0
    r, c = startPos[0], startPos[1]
    while r != homePos[0]:
        r += 1 if homePos[0] > r else -1
        ans += rowCosts[r]
    while c != homePos[1]:
        c += 1 if homePos[1] > c else -1
        ans += colCosts[c]
    return ans

Rust

impl Solution {
    pub fn min_cost(start_pos: Vec<i32>, home_pos: Vec<i32>, row_costs: Vec<i32>, col_costs: Vec<i32>) -> i32 {
        let mut ans = 0;
        let (mut r, mut c) = (start_pos[0], start_pos[1]);
        while r != home_pos[0] {
            r += if home_pos[0] > r { 1 } else { -1 };
            ans += row_costs[r as usize];
        }
        while c != home_pos[1] {
            c += if home_pos[1] > c { 1 } else { -1 };
            ans += col_costs[c as usize];
        }
        ans
    }
}

TypeScript

class Solution {
    minCost(startPos: number[], homePos: number[], rowCosts: number[], colCosts: number[]): number {
        let ans = 0;
        let r = StartPos[0], c = StartPos[1];
        while (r !== homePos[0]) {
            r += homePos[0] > r ? 1 : -1;
            ans += rowCosts[r];
        }
        while (c !== homePos[1]) {
            c += homePos[1] > c ? 1 : -1;
            ans += colCosts[c];
        }
        return ans;
    }
}

Complexity

⏰ Time complexity: O(|rowDiff| + |colDiff|), since we only traverse the difference in rows and columns.
🧺 Space complexity: O(1), only a few variables are used for calculation.