Problem

You are given a positive integer n representing n cities numbered from 1 to n. You are also given a 2D array roads, where roads[i] = [ai, bi, costi] indicates that there is a bidirectional road between cities ai and bi with a cost of traveling equal to costi.

You can buy apples in any city you want, but some cities have different costs to buy apples. You are given the 1-based array appleCost where appleCost[i] is the cost of buying one apple from city i.

You start at some city, traverse through various roads, and eventually buy exactly one apple from any city. After you buy that apple, you have to return back to the city you started at, but now the cost of all the roads will be multiplied by a given factor k.

Given the integer k, return a 1-based arrayanswer of sizen whereanswer[i]_is theminimum total cost to buy an apple if you start at city _i.

Examples

Example 1:

1
2
3
4
5
6
7
8

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2400-2499/2473.Minimum%20Cost%20to%20Buy%20Apples/images/graph55.png)
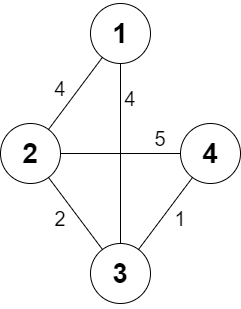
Input: n = 4, roads = [[1,2,4],[2,3,2],[2,4,5],[3,4,1],[1,3,4]], appleCost = [56,42,102,301], k = 2
Output: [54,42,48,51]
Explanation: The minimum cost for each starting city is the following:
- Starting at city 1: You take the path 1 -> 2, buy an apple at city 2, and finally take the path 2 -> 1. The total cost is 4 + 42 + 4 * 2 = 54.
- Starting at city 2: You directly buy an apple at city 2. The total cost is 42.
- Starting at city 3: You take the path 3 -> 2, buy an apple at city 2, and finally take the path 2 -> 3. The total cost is 2 + 42 + 2 * 2 = 48.
- Starting at city 4: You take the path 4 -> 3 -> 2 then you buy at city 2, and finally take the path 2 -> 3 -> 4. The total cost is 1 + 2 + 42 + 1 * 2 + 2 * 2 = 51.

Example 2:

1
2
3
4

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2400-2499/2473.Minimum%20Cost%20to%20Buy%20Apples/images/graph4.png)
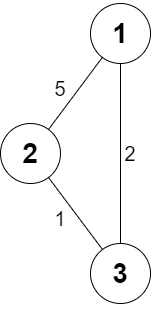
Input: n = 3, roads = [[1,2,5],[2,3,1],[3,1,2]], appleCost = [2,3,1], k = 3
Output: [2,3,1]
Explanation: It is always optimal to buy the apple in the starting city.

Constraints:

  • 2 <= n <= 1000
  • 1 <= roads.length <= 2000
  • 1 <= ai, bi <= n
  • ai != bi
  • 1 <= costi <= 10^5
  • appleCost.length == n
  • 1 <= appleCost[i] <= 10^5
  • 1 <= k <= 100
  • There are no repeated edges.

Solution

Method 1 – Dijkstra’s Algorithm (Two-Phase)

Intuition

We need to find the minimum cost for each city to buy an apple and return, considering the cost of roads changes after buying the apple. The best way is to use Dijkstra’s algorithm twice: once for the trip to the apple city (normal cost), and once for the return trip (cost multiplied by k).

Approach

  1. For each city, run Dijkstra’s algorithm to find the shortest path to every other city (normal cost).
  2. For each city, run Dijkstra’s algorithm again with all road costs multiplied by k (return trip).
  3. For each starting city:
    • For every possible apple city, calculate: cost to reach + apple cost + cost to return.
    • Take the minimum over all apple cities.
  4. Return the answer array.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

class Solution {
public:
    vector<long long> minimumCost(int n, vector<vector<int>>& roads, vector<int>& appleCost, int k) {
        vector<vector<pair<int, int>>> g(n);
        for (auto& r : roads) {
            g[r[0]-1].push_back({r[1]-1, r[2]});
            g[r[1]-1].push_back({r[0]-1, r[2]});
        }
        auto dijkstra = [&](int start, int mul) {
            vector<long long> dist(n, LLONG_MAX);
            priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<>> pq;
            dist[start] = 0;
            pq.push({0, start});
            while (!pq.empty()) {
                auto [d, u] = pq.top(); pq.pop();
                if (d > dist[u]) continue;
                for (auto& [v, w] : g[u]) {
                    long long nd = d + w * mul;
                    if (nd < dist[v]) {
                        dist[v] = nd;
                        pq.push({nd, v});
                    }
                }
            }
            return dist;
        };
        vector<vector<long long>> to(n), back(n);
        for (int i = 0; i < n; ++i) {
            to[i] = dijkstra(i, 1);
            back[i] = dijkstra(i, k);
        }
        vector<long long> ans(n, LLONG_MAX);
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                ans[i] = min(ans[i], to[i][j] + appleCost[j] + back[j][i]);
            }
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

func minimumCost(n int, roads [][]int, appleCost []int, k int) []int64 {
    g := make([][][2]int, n)
    for _, r := range roads {
        g[r[0]-1] = append(g[r[0]-1], [2]int{r[1]-1, r[2]})
        g[r[1]-1] = append(g[r[1]-1], [2]int{r[0]-1, r[2]})
    }
    dijkstra := func(start, mul int) []int64 {
        dist := make([]int64, n)
        for i := range dist { dist[i] = 1<<62 }
        dist[start] = 0
        pq := &heapMin{}; heap.Init(pq)
        heap.Push(pq, node{0, start})
        for pq.Len() > 0 {
            cur := heap.Pop(pq).(node)
            if cur.d > dist[cur.u] { continue }
            for _, e := range g[cur.u] {
                nd := cur.d + int64(e[1])*int64(mul)
                if nd < dist[e[0]] {
                    dist[e[0]] = nd
                    heap.Push(pq, node{nd, e[0]})
                }
            }
        }
        return dist
    }
    to := make([][]int64, n)
    back := make([][]int64, n)
    for i := 0; i < n; i++ {
        to[i] = dijkstra(i, 1)
        back[i] = dijkstra(i, k)
    }
    ans := make([]int64, n)
    for i := 0; i < n; i++ {
        ans[i] = 1<<62
        for j := 0; j < n; j++ {
            v := to[i][j] + int64(appleCost[j]) + back[j][i]
            if v < ans[i] { ans[i] = v }
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

class Solution {
    public long[] minimumCost(int n, int[][] roads, int[] appleCost, int k) {
        List<int[]>[] g = new ArrayList[n];
        for (int i = 0; i < n; ++i) g[i] = new ArrayList<>();
        for (int[] r : roads) {
            g[r[0]-1].add(new int[]{r[1]-1, r[2]});
            g[r[1]-1].add(new int[]{r[0]-1, r[2]});
        }
        long[][] to = new long[n][n], back = new long[n][n];
        for (int i = 0; i < n; ++i) {
            to[i] = dijkstra(g, i, 1);
            back[i] = dijkstra(g, i, k);
        }
        long[] ans = new long[n];
        Arrays.fill(ans, Long.MAX_VALUE);
        for (int i = 0; i < n; ++i)
            for (int j = 0; j < n; ++j)
                ans[i] = Math.min(ans[i], to[i][j] + appleCost[j] + back[j][i]);
        return ans;
    }
    long[] dijkstra(List<int[]>[] g, int start, int mul) {
        int n = g.length;
        long[] dist = new long[n];
        Arrays.fill(dist, Long.MAX_VALUE);
        dist[start] = 0;
        PriorityQueue<long[]> pq = new PriorityQueue<>(Comparator.comparingLong(a->a[0]));
        pq.offer(new long[]{0, start});
        while (!pq.isEmpty()) {
            long[] cur = pq.poll();
            if (cur[0] > dist[(int)cur[1]]) continue;
            for (int[] e : g[(int)cur[1]]) {
                long nd = cur[0] + e[1]*mul;
                if (nd < dist[e[0]]) {
                    dist[e[0]] = nd;
                    pq.offer(new long[]{nd, e[0]});
                }
            }
        }
        return dist;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

class Solution {
    fun minimumCost(n: Int, roads: Array<IntArray>, appleCost: IntArray, k: Int): LongArray {
        val g = Array(n) { mutableListOf<Pair<Int, Int>>() }
        for (r in roads) {
            g[r[0]-1].add(Pair(r[1]-1, r[2]))
            g[r[1]-1].add(Pair(r[0]-1, r[2]))
        }
        fun dijkstra(start: Int, mul: Int): LongArray {
            val dist = LongArray(n) { Long.MAX_VALUE }
            val pq = PriorityQueue(compareBy<Pair<Long, Int>> { it.first })
            dist[start] = 0L
            pq.add(Pair(0L, start))
            while (pq.isNotEmpty()) {
                val (d, u) = pq.poll()
                if (d > dist[u]) continue
                for ((v, w) in g[u]) {
                    val nd = d + w * mul
                    if (nd < dist[v]) {
                        dist[v] = nd
                        pq.add(Pair(nd, v))
                    }
                }
            }
            return dist
        }
        val to = Array(n) { dijkstra(it, 1) }
        val back = Array(n) { dijkstra(it, k) }
        val ans = LongArray(n) { Long.MAX_VALUE }
        for (i in 0 until n) {
            for (j in 0 until n) {
                ans[i] = minOf(ans[i], to[i][j] + appleCost[j] + back[j][i])
            }
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class Solution:
    def minimumCost(self, n: int, roads: list[list[int]], appleCost: list[int], k: int) -> list[int]:
        import heapq
        def dijkstra(start: int, mul: int) -> list[int]:
            dist = [float('inf')] * n
            dist[start] = 0
            pq: list[tuple[int, int]] = [(0, start)]
            while pq:
                d, u = heapq.heappop(pq)
                if d > dist[u]: continue
                for v, w in g[u]:
                    nd = d + w * mul
                    if nd < dist[v]:
                        dist[v] = nd
                        heapq.heappush(pq, (nd, v))
            return dist
        g = [[] for _ in range(n)]
        for a, b, c in roads:
            g[a-1].append((b-1, c))
            g[b-1].append((a-1, c))
        to = [dijkstra(i, 1) for i in range(n)]
        back = [dijkstra(i, k) for i in range(n)]
        ans = [float('inf')] * n
        for i in range(n):
            for j in range(n):
                v = to[i][j] + appleCost[j] + back[j][i]
                if v < ans[i]: ans[i] = v
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

impl Solution {
    pub fn minimum_cost(n: i32, roads: Vec<Vec<i32>>, apple_cost: Vec<i32>, k: i32) -> Vec<i64> {
        use std::collections::BinaryHeap;
        let n = n as usize;
        let mut g = vec![vec![]; n];
        for r in &roads {
            g[(r[0]-1) as usize].push(((r[1]-1) as usize, r[2]));
            g[(r[1]-1) as usize].push(((r[0]-1) as usize, r[2]));
        }
        let dijkstra = |start: usize, mul: i32| -> Vec<i64> {
            let mut dist = vec![i64::MAX; n];
            let mut pq = BinaryHeap::new();
            dist[start] = 0;
            pq.push((std::cmp::Reverse(0), start));
            while let Some((std::cmp::Reverse(d), u)) = pq.pop() {
                if d > dist[u] { continue; }
                for &(v, w) in &g[u] {
                    let nd = d + (w as i64) * (mul as i64);
                    if nd < dist[v] {
                        dist[v] = nd;
                        pq.push((std::cmp::Reverse(nd), v));
                    }
                }
            }
            dist
        };
        let mut to = vec![vec![0; n]; n];
        let mut back = vec![vec![0; n]; n];
        for i in 0..n {
            to[i] = dijkstra(i, 1);
            back[i] = dijkstra(i, k);
        }
        let mut ans = vec![i64::MAX; n];
        for i in 0..n {
            for j in 0..n {
                let v = to[i][j] + apple_cost[j] as i64 + back[j][i];
                if v < ans[i] { ans[i] = v; }
            }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

class Solution {
    minimumCost(n: number, roads: number[][], appleCost: number[], k: number): number[] {
        const g: [number, number][][] = Array.from({length: n}, () => []);
        for (const [a, b, c] of roads) {
            g[a-1].push([b-1, c]);
            g[b-1].push([a-1, c]);
        }
        function dijkstra(start: number, mul: number): number[] {
            const dist = Array(n).fill(Infinity);
            dist[start] = 0;
            const pq: [number, number][] = [[0, start]];
            while (pq.length) {
                pq.sort((a, b) => a[0] - b[0]);
                const [d, u] = pq.shift()!;
                if (d > dist[u]) continue;
                for (const [v, w] of g[u]) {
                    const nd = d + w * mul;
                    if (nd < dist[v]) {
                        dist[v] = nd;
                        pq.push([nd, v]);
                    }
                }
            }
            return dist;
        }
        const to = Array.from({length: n}, (_, i) => dijkstra(i, 1));
        const back = Array.from({length: n}, (_, i) => dijkstra(i, k));
        const ans = Array(n).fill(Infinity);
        for (let i = 0; i < n; ++i) {
            for (let j = 0; j < n; ++j) {
                const v = to[i][j] + appleCost[j] + back[j][i];
                if v < ans[i]) ans[i] = v;
            }
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n^2 log n + n^2) where n is the number of cities. Each Dijkstra run is O(n log n + m) and we run it 2n times.
  • 🧺 Space complexity: O(n^2) for storing all distances.