Problem

There is a country of n cities numbered from 0 to n - 1 where all the cities are connected by bi-directional roads. The roads are represented as a 2D integer array edges where edges[i] = [xi, yi, timei] denotes a road between cities xi and yi that takes timei minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.

Each time you pass through a city, you must pay a passing fee. This is represented as a 0-indexed integer array passingFees of length n where passingFees[j] is the amount of dollars you must pay when you pass through city j.

In the beginning, you are at city 0 and want to reach city n - 1 in maxTimeminutes or less. The cost of your journey is the summation of passing fees for each city that you passed through at some moment of your journey (including the source and destination cities).

Given maxTime, edges, and passingFees, return _theminimum cost to complete your journey, or _-1 if you cannot complete it withinmaxTime minutes.

Examples

Example 1

1
2
3
4
5
6
7
8
9


![](https://assets.leetcode.com/uploads/2021/06/04/leetgraph1-1.png)

    
    
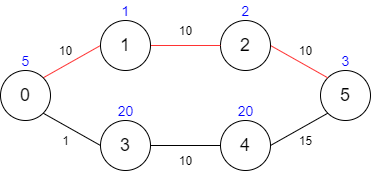
    Input: maxTime = 30, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
    Output: 11
    Explanation: The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.

Example 2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


**![](https://assets.leetcode.com/uploads/2021/06/04/copy-of-
leetgraph1-1.png)**

    
    
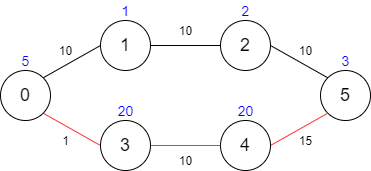    Input: maxTime = 29, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
    Output: 48
    Explanation: The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
    You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.

Example 3

1
2
3
4
5
6
7


    
    
    Input: maxTime = 25, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
    Output: -1
    Explanation: There is no way to reach city 5 from city 0 within 25 minutes.

Constraints

  • 1 <= maxTime <= 1000
  • n == passingFees.length
  • 2 <= n <= 1000
  • n - 1 <= edges.length <= 1000
  • 0 <= xi, yi <= n - 1
  • 1 <= timei <= 1000
  • 1 <= passingFees[j] <= 1000
  • The graph may contain multiple edges between two nodes.
  • The graph does not contain self loops.

Solution

Method 1 – Dijkstra’s Algorithm with Time State

Intuition

We need to find the minimum cost to reach the destination within a time limit, where each city has a passing fee. Since the time spent on each path matters, we use Dijkstra’s algorithm with an extra state for time spent so far.

Approach

  1. Build the graph from the edges list.
  2. Use Dijkstra’s algorithm, where each state is (city, time_spent).
  3. For each edge, if moving to the next city does not exceed maxTime, update the cost and push the new state to the heap.
  4. Track the minimum cost to reach each (city, time_spent).
  5. The answer is the minimum cost to reach city n-1 within maxTime.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class Solution {
public:
    int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {
        int n = passingFees.size();
        vector<vector<pair<int,int>>> g(n);
        for (auto& e : edges) {
            g[e[0]].push_back({e[1], e[2]});
            g[e[1]].push_back({e[0], e[2]});
        }
        vector<vector<int>> cost(n, vector<int>(maxTime+1, INT_MAX));
        priority_queue<tuple<int,int,int>, vector<tuple<int,int,int>>, greater<>> pq;
        cost[0][0] = passingFees[0];
        pq.push({passingFees[0], 0, 0});
        while (!pq.empty()) {
            auto [c, u, t] = pq.top(); pq.pop();
            if (c > cost[u][t]) continue;
            for (auto& [v, w] : g[u]) {
                if (t + w <= maxTime && c + passingFees[v] < cost[v][t+w]) {
                    cost[v][t+w] = c + passingFees[v];
                    pq.push({cost[v][t+w], v, t+w});
                }
            }
        }
        int ans = INT_MAX;
        for (int t = 0; t <= maxTime; ++t) ans = min(ans, cost[n-1][t]);
        return ans == INT_MAX ? -1 : ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

func minCost(maxTime int, edges [][]int, passingFees []int) int {
    n := len(passingFees)
    g := make([][][2]int, n)
    for _, e := range edges {
        g[e[0]] = append(g[e[0]], [2]int{e[1], e[2]})
        g[e[1]] = append(g[e[1]], [2]int{e[0], e[2]})
    }
    cost := make([][]int, n)
    for i := range cost {
        cost[i] = make([]int, maxTime+1)
        for j := range cost[i] { cost[i][j] = 1<<31 - 1 }
    }
    pq := &heapMin{}; heap.Init(pq)
    cost[0][0] = passingFees[0]
    heap.Push(pq, node{passingFees[0], 0, 0})
    for pq.Len() > 0 {
        cur := heap.Pop(pq).(node)
        if cur.c > cost[cur.u][cur.t] { continue }
        for _, e := range g[cur.u] {
            v, w := e[0], e[1]
            if cur.t+w <= maxTime && cur.c+passingFees[v] < cost[v][cur.t+w] {
                cost[v][cur.t+w] = cur.c+passingFees[v]
                heap.Push(pq, node{cost[v][cur.t+w], v, cur.t+w})
            }
        }
    }
    ans := 1<<31 - 1
    for t := 0; t <= maxTime; t++ {
        if cost[n-1][t] < ans { ans = cost[n-1][t] }
    }
    if ans == 1<<31 - 1 { return -1 } else { return ans }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

class Solution {
    public int minCost(int maxTime, int[][] edges, int[] passingFees) {
        int n = passingFees.length;
        List<int[]>[] g = new ArrayList[n];
        for (int i = 0; i < n; ++i) g[i] = new ArrayList<>();
        for (int[] e : edges) {
            g[e[0]].add(new int[]{e[1], e[2]});
            g[e[1]].add(new int[]{e[0], e[2]});
        }
        int[][] cost = new int[n][maxTime+1];
        for (int[] row : cost) Arrays.fill(row, Integer.MAX_VALUE);
        PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a->a[0]));
        cost[0][0] = passingFees[0];
        pq.offer(new int[]{passingFees[0], 0, 0});
        while (!pq.isEmpty()) {
            int[] cur = pq.poll();
            int c = cur[0], u = cur[1], t = cur[2];
            if (c > cost[u][t]) continue;
            for (int[] e : g[u]) {
                int v = e[0], w = e[1];
                if (t + w <= maxTime && c + passingFees[v] < cost[v][t+w]) {
                    cost[v][t+w] = c + passingFees[v];
                    pq.offer(new int[]{cost[v][t+w], v, t+w});
                }
            }
        }
        int ans = Integer.MAX_VALUE;
        for (int t = 0; t <= maxTime; ++t) ans = Math.min(ans, cost[n-1][t]);
        return ans == Integer.MAX_VALUE ? -1 : ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class Solution {
    fun minCost(maxTime: Int, edges: Array<IntArray>, passingFees: IntArray): Int {
        val n = passingFees.size
        val g = Array(n) { mutableListOf<Pair<Int,Int>>() }
        for (e in edges) {
            g[e[0]].add(Pair(e[1], e[2]))
            g[e[1]].add(Pair(e[0], e[2]))
        }
        val cost = Array(n) { IntArray(maxTime+1) { Int.MAX_VALUE } }
        val pq = PriorityQueue(compareBy<Pair<Int,Pair<Int,Int>>> { it.first })
        cost[0][0] = passingFees[0]
        pq.add(Pair(passingFees[0], Pair(0,0)))
        while (pq.isNotEmpty()) {
            val (c, p) = pq.poll()
            val (u, t) = p
            if (c > cost[u][t]) continue
            for ((v, w) in g[u]) {
                if (t + w <= maxTime && c + passingFees[v] < cost[v][t+w]) {
                    cost[v][t+w] = c + passingFees[v]
                    pq.add(Pair(cost[v][t+w], Pair(v, t+w)))
                }
            }
        }
        var ans = Int.MAX_VALUE
        for (t in 0..maxTime) ans = minOf(ans, cost[n-1][t])
        return if (ans == Int.MAX_VALUE) -1 else ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class Solution:
    def minCost(self, maxTime: int, edges: list[list[int]], passingFees: list[int]) -> int:
        import heapq
        n = len(passingFees)
        g = [[] for _ in range(n)]
        for a, b, w in edges:
            g[a].append((b, w))
            g[b].append((a, w))
        cost = [[float('inf')] * (maxTime+1) for _ in range(n)]
        cost[0][0] = passingFees[0]
        pq: list[tuple[int, int, int]] = [(passingFees[0], 0, 0)]
        while pq:
            c, u, t = heapq.heappop(pq)
            if c > cost[u][t]: continue
            for v, w in g[u]:
                if t + w <= maxTime and c + passingFees[v] < cost[v][t+w]:
                    cost[v][t+w] = c + passingFees[v]
                    heapq.heappush(pq, (cost[v][t+w], v, t+w))
        ans = min(cost[-1])
        return -1 if ans == float('inf') else ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

impl Solution {
    pub fn min_cost(max_time: i32, edges: Vec<Vec<i32>>, passing_fees: Vec<i32>) -> i32 {
        use std::collections::BinaryHeap;
        let n = passing_fees.len();
        let mut g = vec![vec![]; n];
        for e in &edges {
            g[e[0] as usize].push((e[1] as usize, e[2]));
            g[e[1] as usize].push((e[0] as usize, e[2]));
        }
        let mut cost = vec![vec![i32::MAX; (max_time+1) as usize]; n];
        cost[0][0] = passing_fees[0];
        let mut pq = BinaryHeap::new();
        pq.push(std::cmp::Reverse((passing_fees[0], 0, 0)));
        while let Some(std::cmp::Reverse((c, u, t))) = pq.pop() {
            if c > cost[u][t as usize] { continue; }
            for &(v, w) in &g[u] {
                if t + w <= max_time && c + passing_fees[v] < cost[v][(t+w) as usize] {
                    cost[v][(t+w) as usize] = c + passing_fees[v];
                    pq.push(std::cmp::Reverse((cost[v][(t+w) as usize], v, t+w)));
                }
            }
        }
        let ans = *cost[n-1].iter().min().unwrap();
        if ans == i32::MAX { -1 } else { ans }
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
    minCost(maxTime: number, edges: number[][], passingFees: number[]): number {
        const n = passingFees.length;
        const g: [number, number][][] = Array.from({length: n}, () => []);
        for (const [a, b, w] of edges) {
            g[a].push([b, w]);
            g[b].push([a, w]);
        }
        const cost: number[][] = Array.from({length: n}, () => Array(maxTime+1).fill(Infinity));
        cost[0][0] = passingFees[0];
        const pq: [number, number, number][] = [[passingFees[0], 0, 0]];
        while (pq.length) {
            pq.sort((a, b) => a[0] - b[0]);
            const [c, u, t] = pq.shift()!;
            if (c > cost[u][t]) continue;
            for (const [v, w] of g[u]) {
                if (t + w <= maxTime && c + passingFees[v] < cost[v][t+w]) {
                    cost[v][t+w] = c + passingFees[v];
                    pq.push([cost[v][t+w], v, t+w]);
                }
            }
        }
        const ans = Math.min(...cost[n-1]);
        return ans === Infinity ? -1 : ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n * maxTime * log(n * maxTime)) where n is the number of cities.
  • 🧺 Space complexity: O(n * maxTime) for the cost table.