Minimum Costs Using the Train Line

Problem

A train line going through a city has two routes, the regular route and the express route. Both routes go through the same n + 1 stops labeled from 0 to n. Initially, you start on the regular route at stop 0.

You are given two 1-indexed integer arrays regular and express, both of length n. regular[i] describes the cost it takes to go from stop i -1 to stop i using the regular route, and express[i] describes the cost it takes to go from stop i - 1 to stop i using the express route.

You are also given an integer expressCost which represents the cost to transfer from the regular route to the express route.

Note that:

• There is no cost to transfer from the express route back to the regular route.
• You pay expressCost every time you transfer from the regular route to the express route.
• There is no extra cost to stay on the express route.

Return _a1-indexed array _costs of lengthn , wherecosts[i]_is theminimum cost to reach stop _i from stop0.

Note that a stop can be counted as reached from either route.

Examples

Example 1:

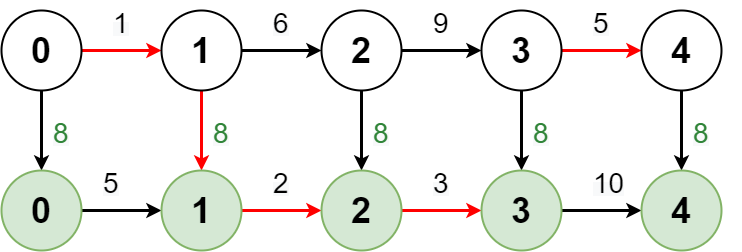
Input: regular = [1,6,9,5], express = [5,2,3,10], expressCost = 8
Output: [1,7,14,19]
Explanation: The diagram above shows how to reach stop 4 from stop 0 with minimum cost.
- Take the regular route from stop 0 to stop 1, costing 1.
- Take the express route from stop 1 to stop 2, costing 8 + 2 = 10.
- Take the express route from stop 2 to stop 3, costing 3.
- Take the regular route from stop 3 to stop 4, costing 5.
The total cost is 1 + 10 + 3 + 5 = 19.
Note that a different route could be taken to reach the other stops with minimum cost.

Example 2:

Input: regular = [11,5,13], express = [7,10,6], expressCost = 3
Output: [10,15,24]
Explanation: The diagram above shows how to reach stop 3 from stop 0 with minimum cost.
- Take the express route from stop 0 to stop 1, costing 3 + 7 = 10.
- Take the regular route from stop 1 to stop 2, costing 5.
- Take the express route from stop 2 to stop 3, costing 3 + 6 = 9.
The total cost is 10 + 5 + 9 = 24.
Note that the expressCost is paid again to transfer back to the express route.

Constraints:

• n == regular.length == express.length
• 1 <= n <= 10^5
• 1 <= regular[i], express[i], expressCost <= 10^5

Solution

Method 1 – Dynamic Programming (Two States)

Intuition

We use dynamic programming to track the minimum cost to reach each stop on both the regular and express routes. At each stop, we can either continue on the same route or transfer (from regular to express, paying the transfer cost). We update the minimum cost for both routes at each stop and take the minimum for the answer.

Approach

1. Initialize two arrays: reg and exp, where reg[i] is the minimum cost to reach stop i on the regular route, and exp[i] is the minimum cost to reach stop i on the express route.
2. Set reg[0] = 0 and exp[0] = inf (can't start on express).
3. For each stop i from 1 to n:
   • Update reg[i] as the minimum of continuing on regular or switching from express to regular.
   • Update exp[i] as the minimum of continuing on express or transferring from regular to express (paying transfer cost).
4. For each stop, the answer is the minimum of reg[i] and exp[i].

Code

C++

class Solution {
public:
    vector<long long> minimumCosts(vector<int>& regular, vector<int>& express, int expressCost) {
        int n = regular.size();
        vector<long long> reg(n+1, LLONG_MAX), exp(n+1, LLONG_MAX), ans(n);
        reg[0] = 0;
        for (int i = 1; i <= n; ++i) {
            reg[i] = min(reg[i-1] + regular[i-1], exp[i-1] + regular[i-1]);
            exp[i] = min(exp[i-1] + express[i-1], reg[i-1] + express[i-1] + expressCost);
            ans[i-1] = min(reg[i], exp[i]);
        }
        return ans;
    }
};

Go

func minimumCosts(regular, express []int, expressCost int) []int64 {
    n := len(regular)
    reg := make([]int64, n+1)
    exp := make([]int64, n+1)
    for i := range reg { reg[i], exp[i] = 1<<62, 1<<62 }
    reg[0] = 0
    ans := make([]int64, n)
    for i := 1; i <= n; i++ {
        reg[i] = min(reg[i-1]+int64(regular[i-1]), exp[i-1]+int64(regular[i-1]))
        exp[i] = min(exp[i-1]+int64(express[i-1]), reg[i-1]+int64(express[i-1])+int64(expressCost))
        ans[i-1] = min(reg[i], exp[i])
    }
    return ans
}

Java

class Solution {
    public long[] minimumCosts(int[] regular, int[] express, int expressCost) {
        int n = regular.length;
        long[] reg = new long[n+1], exp = new long[n+1], ans = new long[n];
        Arrays.fill(reg, Long.MAX_VALUE);
        Arrays.fill(exp, Long.MAX_VALUE);
        reg[0] = 0;
        for (int i = 1; i <= n; ++i) {
            reg[i] = Math.min(reg[i-1] + regular[i-1], exp[i-1] + regular[i-1]);
            exp[i] = Math.min(exp[i-1] + express[i-1], reg[i-1] + express[i-1] + expressCost);
            ans[i-1] = Math.min(reg[i], exp[i]);
        }
        return ans;
    }
}

Kotlin

class Solution {
    fun minimumCosts(regular: IntArray, express: IntArray, expressCost: Int): LongArray {
        val n = regular.size
        val reg = LongArray(n+1) { Long.MAX_VALUE }
        val exp = LongArray(n+1) { Long.MAX_VALUE }
        val ans = LongArray(n)
        reg[0] = 0L
        for (i in 1..n) {
            reg[i] = minOf(reg[i-1]+regular[i-1], exp[i-1]+regular[i-1])
            exp[i] = minOf(exp[i-1]+express[i-1], reg[i-1]+express[i-1]+expressCost)
            ans[i-1] = minOf(reg[i], exp[i])
        }
        return ans
    }
}

Python

class Solution:
    def minimumCosts(self, regular: list[int], express: list[int], expressCost: int) -> list[int]:
        n = len(regular)
        reg = [float('inf')] * (n+1)
        exp = [float('inf')] * (n+1)
        ans = [0] * n
        reg[0] = 0
        for i in range(1, n+1):
            reg[i] = min(reg[i-1]+regular[i-1], exp[i-1]+regular[i-1])
            exp[i] = min(exp[i-1]+express[i-1], reg[i-1]+express[i-1]+expressCost)
            ans[i-1] = min(reg[i], exp[i])
        return ans

Rust

impl Solution {
    pub fn minimum_costs(regular: Vec<i32>, express: Vec<i32>, express_cost: i32) -> Vec<i64> {
        let n = regular.len();
        let mut reg = vec![i64::MAX; n+1];
        let mut exp = vec![i64::MAX; n+1];
        let mut ans = vec![0; n];
        reg[0] = 0;
        for i in 1..=n {
            reg[i] = (reg[i-1]+regular[i-1] as i64).min(exp[i-1]+regular[i-1] as i64);
            exp[i] = (exp[i-1]+express[i-1] as i64).min(reg[i-1]+express[i-1] as i64+express_cost as i64);
            ans[i-1] = reg[i].min(exp[i]);
        }
        ans
    }
}

TypeScript

class Solution {
    minimumCosts(regular: number[], express: number[], expressCost: number): number[] {
        const n = regular.length;
        const reg = Array(n+1).fill(Infinity);
        const exp = Array(n+1).fill(Infinity);
        const ans = Array(n).fill(0);
        reg[0] = 0;
        for (let i = 1; i <= n; ++i) {
            reg[i] = Math.min(reg[i-1]+regular[i-1], exp[i-1]+regular[i-1]);
            exp[i] = Math.min(exp[i-1]+express[i-1], reg[i-1]+express[i-1]+expressCost);
            ans[i-1] = Math.min(reg[i], exp[i]);
        }
        return ans;
    }
}

Complexity

• ⏰ Time complexity: O(n) where n is the number of stops.
• 🧺 Space complexity: O(n) for the DP arrays.