problemeasyalgorithmsleetcode-2481leetcode 2481leetcode2481

Minimum Cuts to Divide a Circle

EasyUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

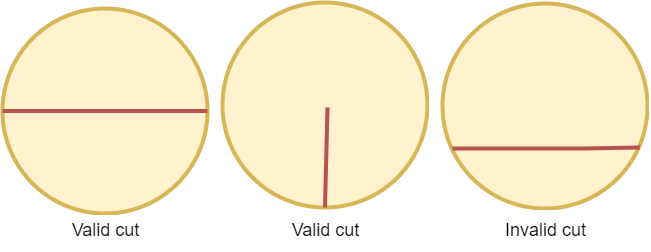
A valid cut in a circle can be:

  • A cut that is represented by a straight line that touches two points on the edge of the circle and passes through its center, or
  • A cut that is represented by a straight line that touches one point on the edge of the circle and its center.

Some valid and invalid cuts are shown in the figures below.

Given the integer n, return _theminimum number of cuts needed to divide a circle into _n equal slices.

Examples

Example 1

Input: n = 4
Output: 2
Explanation: You can divide the circle into 4 equal slices with 2 cuts passing through the center.

Example 2

Input: n = 3
Output: 3
Explanation: You need 3 cuts passing through the center to divide the circle into 3 equal slices.

Example 3

Input: n = 1
Output: 0
Explanation: No cuts are needed if there is only 1 slice.

Constraints

  • 1 <= n <= 100

Solution

Method 1 – Mathematical Observation

Intuition

If n == 1, no cuts are needed. If n is even, you can divide the circle with n/2 cuts passing through the center. If n is odd, you need n cuts passing through the center.

Approach

  1. If n == 1, return 0.
  2. If n is even, return n/2.
  3. If n is odd, return n.

Code

C++
class Solution {
public:
    int numberOfCuts(int n) {
        if (n == 1) return 0;
        if (n % 2 == 0) return n / 2;
        return n;
    }
};
Go
func numberOfCuts(n int) int {
    if n == 1 { return 0 }
    if n%2 == 0 { return n/2 }
    return n
}
Java
class Solution {
    public int numberOfCuts(int n) {
        if (n == 1) return 0;
        if (n % 2 == 0) return n / 2;
        return n;
    }
}
Kotlin
class Solution {
    fun numberOfCuts(n: Int): Int {
        if (n == 1) return 0
        if (n % 2 == 0) return n / 2
        return n
    }
}
Python
class Solution:
    def numberOfCuts(self, n: int) -> int:
        if n == 1:
            return 0
        if n % 2 == 0:
            return n // 2
        return n
Rust
impl Solution {
    pub fn number_of_cuts(n: i32) -> i32 {
        if n == 1 { 0 } else if n % 2 == 0 { n / 2 } else { n }
    }
}
TypeScript
class Solution {
    numberOfCuts(n: number): number {
        if (n === 1) return 0;
        if (n % 2 === 0) return n / 2;
        return n;
    }
}

Complexity

  • ⏰ Time complexity: O(1) for all cases.
  • 🧺 Space complexity: O(1) for all cases.

Comments