problemmediumalgorithmsleetcode-1007leetcode 1007leetcode1007

Minimum Domino Rotations For Equal Row

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

In a row of dominoes, tops[i] and bottoms[i] represent the top and bottom halves of the ith domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)

We may rotate the ith domino, so that tops[i] and bottoms[i] swap values.

Return the minimum number of rotations so that all the values in tops are the same, or all the values in bottoms are the same.

If it cannot be done, return -1.

Examples

Example 1:


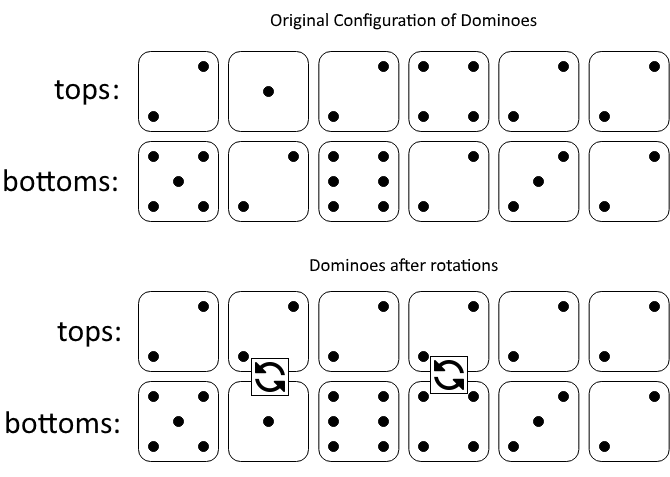
![](https://assets.leetcode.com/uploads/2021/05/14/domino.png)

Input: tops = [2,1,2,4,2,2], bottoms = [5,2,6,2,3,2]
Output: 2
Explanation: 
The first figure represents the dominoes as given by tops and bottoms: before we do any rotations.
If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.

Example 2:

Input: tops = [3,5,1,2,3], bottoms = [3,6,3,3,4]
Output: -1
Explanation: 
In this case, it is not possible to rotate the dominoes to make one row of values equal.

Constraints:

  • 2 <= tops.length <= 2 * 104
  • bottoms.length == tops.length
  • 1 <= tops[i], bottoms[i] <= 6

Solution

The goal is to find the minimum number of rotations required to make all values in the tops array the same, or all values in the bottoms array the same. Domino rotations involve swapping the values at a specific index between tops and bottoms.

Method 1 - Greedy

Approach:

  1. Identify Potential Candidates:
    • For a uniform row, the candidate value must come from either the first domino's tops[0] or bottoms[0]. These two values are the only possible candidates for rotation.
  2. Count Rotations Needed:
    • Evaluate the rotation separately for the candidate value tops[0]:
      • Count how many rotations are needed to make either all tops entries equal to this value or all bottoms entries equal to this value.
    • Repeat the above process for the candidate value bottoms[0].
  3. Check Validity:
    • If either candidate value cannot achieve uniformity in either tops or bottoms across the entire row, return -1.

Reasoning:

  • The choice of candidates is limited to tops[0] or bottoms[0] because these values must appear in all tops or all bottoms for a row to be uniform after rotations.
  • Measure rotations for both candidates and return the minimum count required.

Code

Java
class Solution {

    public int minDominoRotations(int[] tops, int[] bottoms) {
        int ansTop = check(tops, bottoms, tops[0]);
        int ansBottom = check(tops, bottoms, bottoms[0]);

        if (ansTop == -1 && ansBottom == -1) {
            return -1;
        } else if (ansTop == -1) {
            return ansBottom;
        } else if (ansBottom == -1) {
            return ansTop;
        }

        return Math.min(ansTop, ansBottom);
    }

    private int check(int[] tops, int[] bottoms, int x) {
        int tRot = 0, bRot = 0;
        for (int i = 0; i < tops.length; i++) {
            if (tops[i] != x && bottoms[i] != x) {
                return -1;
            } else if (tops[i] != x) {
                tRot++;
            } else if (bottoms[i] != x) {
                bRot++;
            }
        }
        return Math.min(tRot, bRot);
    }
}
Python
class Solution:
    def minDominoRotations(self, tops: List[int], bottoms: List[int]) -> int:
        def check(x: int) -> int:
            t_rot, b_rot = 0, 0
            for t, b in zip(tops, bottoms):
                if t != x and b != x:
                    return -1
                elif t != x:
                    t_rot += 1
                elif b != x:
                    b_rot += 1
            return min(t_rot, b_rot)
        
        ans_top = check(tops[0])
        ans_bottom = check(bottoms[0])
        
        if ans_top == -1 and ans_bottom == -1:
            return -1
        elif ans_top == -1:
            return ans_bottom
        elif ans_bottom == -1:
            return ans_top
        
        return min(ans_top, ans_bottom)

Complexity

  • ⏰ Time complexity: O(n). As we iterate through the arrays once for each candidate, processing every domino in linear time.
  • 🧺 Space complexity: O(1). Only a constant amount of space is used for counters and comparisons.

Comments