Problem

There is a simple directed graph with n nodes labeled from 0 to n -1. The graph would form a tree if its edges were bi-directional.

You are given an integer n and a 2D integer array edges, where edges[i] = [ui, vi] represents a directed edge going from node ui to node vi.

An edge reversal changes the direction of an edge, i.e., a directed edge going from node ui to node vi becomes a directed edge going from node vi to node ui.

For every node i in the range [0, n - 1], your task is to independently calculate the minimum number of edge reversals required so it is possible to reach any other node starting from node i through a sequence of directed edges.

Return an integer arrayanswer , whereanswer[i]is the __ _minimum number of edge reversals required so it is possible to reach any other node starting from node _i through asequence of directed edges.

Examples

Example 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


![](https://assets.leetcode.com/uploads/2023/08/26/image-20230826221104-3.png)

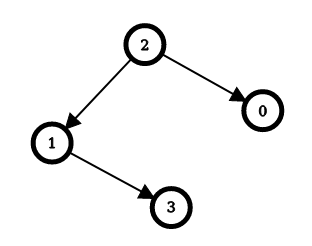
Input: n = 4, edges = [[2,0],[2,1],[1,3]]
Output: [1,1,0,2]
Explanation: The image above shows the graph formed by the edges.
For node 0: after reversing the edge [2,0], it is possible to reach any other node starting from node 0.
So, answer[0] = 1.
For node 1: after reversing the edge [2,1], it is possible to reach any other node starting from node 1.
So, answer[1] = 1.
For node 2: it is already possible to reach any other node starting from node 2.
So, answer[2] = 0.
For node 3: after reversing the edges [1,3] and [2,1], it is possible to reach any other node starting from node 3.
So, answer[3] = 2.

Example 2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


![](https://assets.leetcode.com/uploads/2023/08/26/image-20230826225541-2.png)

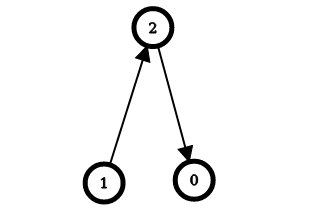
Input: n = 3, edges = [[1,2],[2,0]]
Output: [2,0,1]
Explanation: The image above shows the graph formed by the edges.
For node 0: after reversing the edges [2,0] and [1,2], it is possible to reach any other node starting from node 0.
So, answer[0] = 2.
For node 1: it is already possible to reach any other node starting from node 1.
So, answer[1] = 0.
For node 2: after reversing the edge [1, 2], it is possible to reach any other node starting from node 2.
So, answer[2] = 1.

Constraints

  • 2 <= n <= 10^5
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ui == edges[i][0] < n
  • 0 <= vi == edges[i][1] < n
  • ui != vi
  • The input is generated such that if the edges were bi-directional, the graph would be a tree.

Solution

Method 1 – DFS Rerooting

Intuition

Since the graph is a tree if undirected, we can count the minimum reversals needed for one root using DFS. Then, for each node, we can reroot the tree and update the reversal count efficiently using the parent-child relationship.

Approach

  1. Build an adjacency list, marking each edge as original (0) or reversed (1).
  2. Use DFS from node 0 to count the number of reversals needed to reach all nodes from node 0.
  3. Use a second DFS to reroot the tree at each node, updating the reversal count for each child based on edge direction.
  4. Collect the reversal counts for all nodes.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
public:
    vector<int> minEdgeReversals(int n, vector<vector<int>>& edges) {
        vector<vector<pair<int,int>>> g(n);
        for (auto& e : edges) {
            g[e[0]].push_back({e[1], 0}); // original
            g[e[1]].push_back({e[0], 1}); // reversed
        }
        vector<int> ans(n), vis(n);
        function<int(int)> dfs = [&](int u) {
            vis[u] = 1;
            int cnt = 0;
            for (auto& [v, rev] : g[u]) {
                if (!vis[v]) cnt += rev + dfs(v);
            }
            return cnt;
        };
        ans[0] = dfs(0);
        function<void(int,int)> reroot = [&](int u, int p) {
            vis[u] = 1;
            for (auto& [v, rev] : g[u]) {
                if (!vis[v]) {
                    ans[v] = ans[u] + (rev ? -1 : 1);
                    reroot(v, u);
                }
            }
        };
        fill(vis.begin(), vis.end(), 0);
        reroot(0, -1);
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

func minEdgeReversals(n int, edges [][]int) []int {
    g := make([][][2]int, n)
    for _, e := range edges {
        g[e[0]] = append(g[e[0]], [2]int{e[1], 0})
        g[e[1]] = append(g[e[1]], [2]int{e[0], 1})
    }
    ans := make([]int, n)
    vis := make([]bool, n)
    var dfs func(int) int
    dfs = func(u int) int {
        vis[u] = true
        cnt := 0
        for _, e := range g[u] {
            v, rev := e[0], e[1]
            if !vis[v] {
                cnt += rev + dfs(v)
            }
        }
        return cnt
    }
    ans[0] = dfs(0)
    for i := range vis { vis[i] = false }
    var reroot func(int, int)
    reroot = func(u, p int) {
        vis[u] = true
        for _, e := range g[u] {
            v, rev := e[0], e[1]
            if !vis[v] {
                ans[v] = ans[u] + func() int { if rev == 1 { return -1 } else { return 1 } }()
                reroot(v, u)
            }
        }
    }
    reroot(0, -1)
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

class Solution {
    public int[] minEdgeReversals(int n, int[][] edges) {
        List<int[]>[] g = new ArrayList[n];
        for (int i = 0; i < n; i++) g[i] = new ArrayList<>();
        for (int[] e : edges) {
            g[e[0]].add(new int[]{e[1], 0});
            g[e[1]].add(new int[]{e[0], 1});
        }
        int[] ans = new int[n];
        boolean[] vis = new boolean[n];
        ans[0] = dfs(0, g, vis);
        Arrays.fill(vis, false);
        reroot(0, -1, g, vis, ans);
        return ans;
    }
    private int dfs(int u, List<int[]>[] g, boolean[] vis) {
        vis[u] = true;
        int cnt = 0;
        for (int[] e : g[u]) {
            int v = e[0], rev = e[1];
            if (!vis[v]) cnt += rev + dfs(v, g, vis);
        }
        return cnt;
    }
    private void reroot(int u, int p, List<int[]>[] g, boolean[] vis, int[] ans) {
        vis[u] = true;
        for (int[] e : g[u]) {
            int v = e[0], rev = e[1];
            if (!vis[v]) {
                ans[v] = ans[u] + (rev == 1 ? -1 : 1);
                reroot(v, u, g, vis, ans);
            }
        }
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
    fun minEdgeReversals(n: Int, edges: Array<IntArray>): IntArray {
        val g = Array(n) { mutableListOf<Pair<Int, Int>>() }
        for (e in edges) {
            g[e[0]].add(Pair(e[1], 0))
            g[e[1]].add(Pair(e[0], 1))
        }
        val ans = IntArray(n)
        val vis = BooleanArray(n)
        fun dfs(u: Int): Int {
            vis[u] = true
            var cnt = 0
            for ((v, rev) in g[u]) {
                if (!vis[v]) cnt += rev + dfs(v)
            }
            return cnt
        }
        ans[0] = dfs(0)
        vis.fill(false)
        fun reroot(u: Int, p: Int) {
            vis[u] = true
            for ((v, rev) in g[u]) {
                if (!vis[v]) {
                    ans[v] = ans[u] + if (rev == 1) -1 else 1
                    reroot(v, u)
                }
            }
        }
        reroot(0, -1)
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

def min_edge_reversals(n: int, edges: list[list[int]]) -> list[int]:
    g = [[] for _ in range(n)]
    for u, v in edges:
        g[u].append((v, 0))
        g[v].append((u, 1))
    ans = [0] * n
    vis = [0] * n
    def dfs(u: int) -> int:
        vis[u] = 1
        cnt = 0
        for v, rev in g[u]:
            if not vis[v]:
                cnt += rev + dfs(v)
        return cnt
    ans[0] = dfs(0)
    vis = [0] * n
    def reroot(u: int, p: int):
        vis[u] = 1
        for v, rev in g[u]:
            if not vis[v]:
                ans[v] = ans[u] + ( -1 if rev else 1 )
                reroot(v, u)
    reroot(0, -1)
    return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

impl Solution {
    pub fn min_edge_reversals(n: i32, edges: Vec<Vec<i32>>) -> Vec<i32> {
        let n = n as usize;
        let mut g = vec![vec![]; n];
        for e in edges.iter() {
            g[e[0] as usize].push((e[1] as usize, 0));
            g[e[1] as usize].push((e[0] as usize, 1));
        }
        let mut ans = vec![0; n];
        let mut vis = vec![false; n];
        fn dfs(u: usize, g: &Vec<Vec<(usize, i32)>>, vis: &mut Vec<bool>) -> i32 {
            vis[u] = true;
            let mut cnt = 0;
            for &(v, rev) in &g[u] {
                if !vis[v] {
                    cnt += rev + dfs(v, g, vis);
                }
            }
            cnt
        }
        ans[0] = dfs(0, &g, &mut vis);
        vis.fill(false);
        fn reroot(u: usize, p: isize, g: &Vec<Vec<(usize, i32)>>, vis: &mut Vec<bool>, ans: &mut Vec<i32>) {
            vis[u] = true;
            for &(v, rev) in &g[u] {
                if !vis[v] {
                    ans[v] = ans[u] + if rev == 1 { -1 } else { 1 };
                    reroot(v, u as isize, g, vis, ans);
                }
            }
        }
        reroot(0, -1, &g, &mut vis, &mut ans);
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
    minEdgeReversals(n: number, edges: number[][]): number[] {
        const g: [number, number][][] = Array.from({length: n}, () => []);
        for (const [u, v] of edges) {
            g[u].push([v, 0]);
            g[v].push([u, 1]);
        }
        const ans = Array(n).fill(0);
        const vis = Array(n).fill(false);
        function dfs(u: number): number {
            vis[u] = true;
            let cnt = 0;
            for (const [v, rev] of g[u]) {
                if (!vis[v]) cnt += rev + dfs(v);
            }
            return cnt;
        }
        ans[0] = dfs(0);
        vis.fill(false);
        function reroot(u: number, p: number) {
            vis[u] = true;
            for (const [v, rev] of g[u]) {
                if (!vis[v]) {
                    ans[v] = ans[u] + (rev === 1 ? -1 : 1);
                    reroot(v, u);
                }
            }
        }
        reroot(0, -1);
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n), where n is the number of nodes. Each edge is visited twice (once for each DFS).
  • 🧺 Space complexity: O(n), for adjacency list and answer arrays.