Problem

There is a 1-indexed 8 x 8 chessboard containing 3 pieces.

You are given 6 integers a, b, c, d, e, and f where:

  • (a, b) denotes the position of the white rook.
  • (c, d) denotes the position of the white bishop.
  • (e, f) denotes the position of the black queen.

Given that you can only move the white pieces, return theminimum number of moves required to capture the black queen.

Note that:

  • Rooks can move any number of squares either vertically or horizontally, but cannot jump over other pieces.
  • Bishops can move any number of squares diagonally, but cannot jump over other pieces.
  • A rook or a bishop can capture the queen if it is located in a square that they can move to.
  • The queen does not move.

Examples

Example 1

1
2
3
4
5
6
7


![](https://assets.leetcode.com/uploads/2023/12/21/ex1.png)

Input: a = 1, b = 1, c = 8, d = 8, e = 2, f = 3
Output: 2
Explanation: We can capture the black queen in two moves by moving the white rook to (1, 3) then to (2, 3).
It is impossible to capture the black queen in less than two moves since it is not being attacked by any of the pieces at the beginning.

Example 2

1
2
3
4
5
6
7
8


![](https://assets.leetcode.com/uploads/2023/12/21/ex2.png)

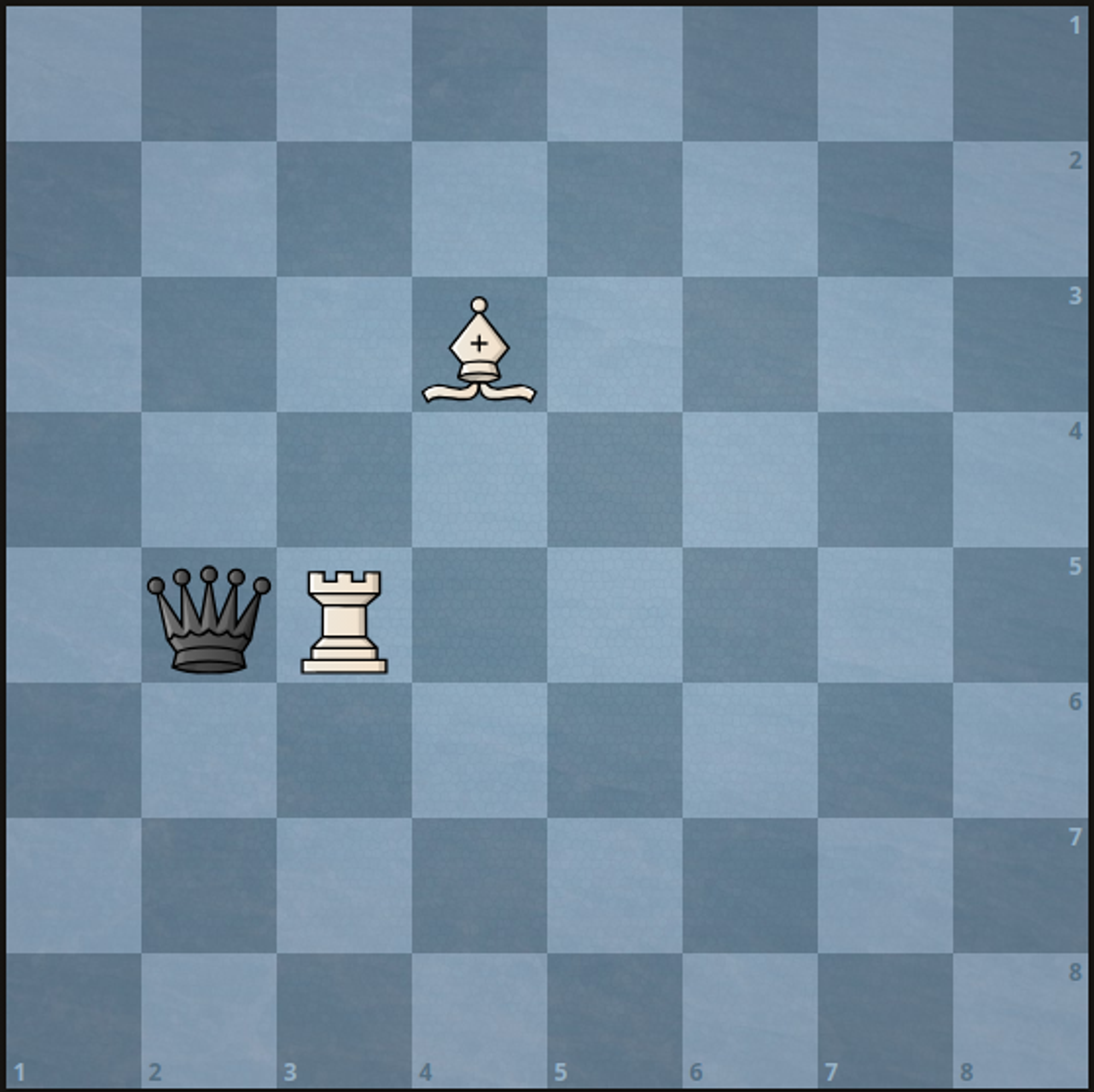
Input: a = 5, b = 3, c = 3, d = 4, e = 5, f = 2
Output: 1
Explanation: We can capture the black queen in a single move by doing one of the following: 
- Move the white rook to (5, 2).
- Move the white bishop to (5, 2).

Constraints

  • 1 <= a, b, c, d, e, f <= 8
  • No two pieces are on the same square.

Solution

Method 1 – Direct Enumeration and Blocking Check

Intuition

The rook and bishop can capture the queen in one move if they are aligned and not blocked by the other piece. Otherwise, it may take two moves. We check all possible cases for both pieces, considering blocking and alignment.

Approach

  1. Check if the rook can capture the queen in one move (same row or column, and not blocked by bishop).
  2. Check if the bishop can capture the queen in one move (same diagonal, and not blocked by rook).
  3. If neither can capture in one move, return 2 (since the board is small, two moves are always enough).

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

class Solution {
public:
    int minMovesToCaptureTheQueen(int a, int b, int c, int d, int e, int f) {
        // Rook one move
        if ((a == e || b == f) && !((a == c && c == e && ((b < d && d < f) || (b > d && d > f))) || (b == d && d == f && ((a < c && c < e) || (a > c && c > e)))))
            return 1;
        // Bishop one move
        if (abs(c - e) == abs(d - f) && !((abs(a - c) == abs(b - d)) && abs(a - e) == abs(b - f) && ((c < a && a < e) || (c > a && a > e))))
            return 1;
        return 2;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

func minMovesToCaptureTheQueen(a, b, c, d, e, f int) int {
    if (a == e || b == f) && !((a == c && c == e && ((b < d && d < f) || (b > d && d > f))) || (b == d && d == f && ((a < c && c < e) || (a > c && c > e)))) {
        return 1
    }
    if abs(c-e) == abs(d-f) && !((abs(a-c) == abs(b-d)) && abs(a-e) == abs(b-f) && ((c < a && a < e) || (c > a && a > e))) {
        return 1
    }
    return 2
}
func abs(x int) int { if x < 0 { return -x }; return x }
1
2
3
4
5
6
7
8
9

class Solution {
    public int minMovesToCaptureTheQueen(int a, int b, int c, int d, int e, int f) {
        if ((a == e || b == f) && !((a == c && c == e && ((b < d && d < f) || (b > d && d > f))) || (b == d && d == f && ((a < c && c < e) || (a > c && c > e)))) )
            return 1;
        if (Math.abs(c-e) == Math.abs(d-f) && !((Math.abs(a-c) == Math.abs(b-d)) && Math.abs(a-e) == Math.abs(b-f) && ((c < a && a < e) || (c > a && a > e))))
            return 1;
        return 2;
    }
}
1
2
3
4
5
6
7
8
9

class Solution {
    fun minMovesToCaptureTheQueen(a: Int, b: Int, c: Int, d: Int, e: Int, f: Int): Int {
        if ((a == e || b == f) && !((a == c && c == e && ((b < d && d < f) || (b > d && d > f))) || (b == d && d == f && ((a < c && c < e) || (a > c && c > e)))) )
            return 1
        if (kotlin.math.abs(c-e) == kotlin.math.abs(d-f) && !((kotlin.math.abs(a-c) == kotlin.math.abs(b-d)) && kotlin.math.abs(a-e) == kotlin.math.abs(b-f) && ((c < a && a < e) || (c > a && a > e))))
            return 1
        return 2
    }
}
1
2
3
4
5
6

def min_moves_to_capture_the_queen(a: int, b: int, c: int, d: int, e: int, f: int) -> int:
    if (a == e or b == f) and not ((a == c == e and ((b < d < f) or (b > d > f))) or (b == d == f and ((a < c < e) or (a > c > e)))):
        return 1
    if abs(c-e) == abs(d-f) and not ((abs(a-c) == abs(b-d)) and abs(a-e) == abs(b-f) and ((c < a < e) or (c > a > e))):
        return 1
    return 2
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

impl Solution {
    pub fn min_moves_to_capture_the_queen(a: i32, b: i32, c: i32, d: i32, e: i32, f: i32) -> i32 {
        if (a == e || b == f) && !((a == c && c == e && ((b < d && d < f) || (b > d && d > f))) || (b == d && d == f && ((a < c && c < e) || (a > c && c > e)))) {
            return 1;
        }
        if ( (c-e).abs() == (d-f).abs() && !((a-c).abs() == (b-d).abs() && (a-e).abs() == (b-f).abs() && ((c < a && a < e) || (c > a && a > e))) ) {
            return 1;
        }
        2
    }
}
1
2
3
4
5
6
7
8
9

class Solution {
    minMovesToCaptureTheQueen(a: number, b: number, c: number, d: number, e: number, f: number): number {
        if ((a === e || b === f) && !((a === c && c === e && ((b < d && d < f) || (b > d && d > f))) || (b === d && d === f && ((a < c && c < e) || (a > c && c > e)))) )
            return 1;
        if (Math.abs(c-e) === Math.abs(d-f) && !((Math.abs(a-c) === Math.abs(b-d)) && Math.abs(a-e) === Math.abs(b-f) && ((c < a && a < e) || (c > a && a > e))))
            return 1;
        return 2;
    }
}

Complexity

  • ⏰ Time complexity: O(1), all checks are constant time.
  • 🧺 Space complexity: O(1), only a few variables are used.