problemmediumalgorithmsleetcode-3189leetcode 3189leetcode3189

Minimum Moves to Get a Peaceful Board

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

Given a 2D array rooks of length n, where rooks[i] = [xi, yi] indicates the position of a rook on an n x n chess board. Your task is to move the rooks 1 cell at a time vertically or horizontally (to an adjacent cell) such that the board becomes peaceful.

A board is peaceful if there is exactly one rook in each row and each column.

Return the minimum number of moves required to get a peaceful board.

Note that at no point can there be two rooks in the same cell.

Examples

Example 1:

Input: rooks = [[0,0],[1,0],[1,1]]
Output: 3
Explanation:
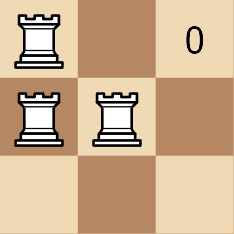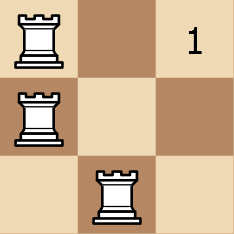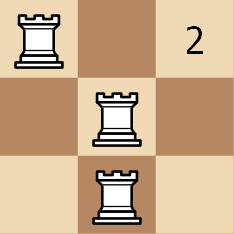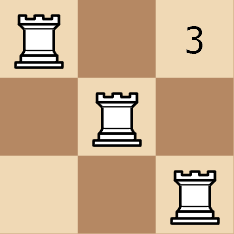
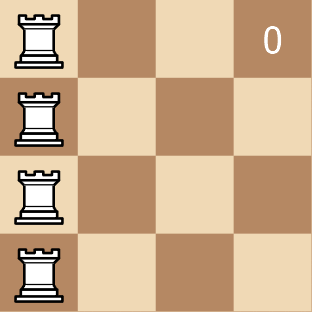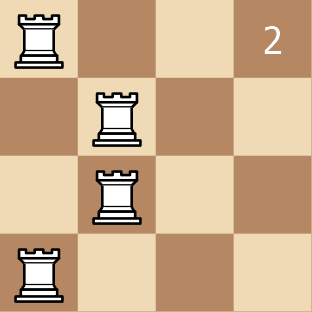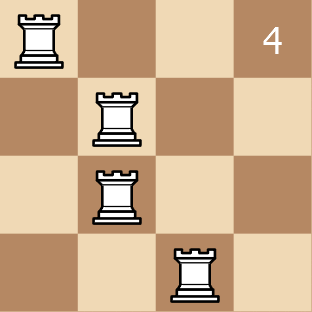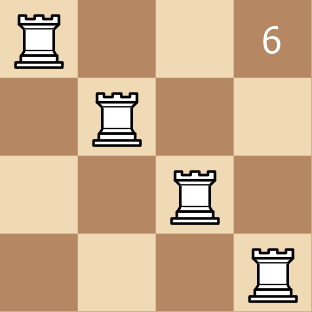
![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/3100-3199/3189.Minimum%20Moves%20to%20Get%20a%20Peaceful%20Board/images/ex1-edited.gif)

Example 2:

Input: rooks = [[0,0],[0,1],[0,2],[0,3]]
Output: 6
Explanation:
![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/3100-3199/3189.Minimum%20Moves%20to%20Get%20a%20Peaceful%20Board/images/ex2-edited.gif)

Constraints:

  • 1 <= n == rooks.length <= 500
  • 0 <= xi, yi <= n - 1
  • The input is generated such that there are no 2 rooks in the same cell.

Solution

Method 1 – Hungarian Algorithm (Minimum Cost Bipartite Matching)

Intuition

To get a peaceful board, we need to assign each rook to a unique row and column. This is equivalent to finding a minimum cost matching between the current positions and the target positions (one rook per row and column). The cost is the Manhattan distance for each assignment.

Approach

  1. Extract the x and y coordinates of all rooks.
  2. Sort the x coordinates and y coordinates independently.
  3. The minimum moves for rows is the sum of absolute differences between sorted x and target rows (0 to n-1).
  4. The minimum moves for columns is the sum of absolute differences between sorted y and target columns (0 to n-1).
  5. The answer is the sum of the two.

Code

C++
class Solution {
public:
    int minMovesToPeacefulBoard(vector<vector<int>>& rooks) {
        int n = rooks.size();
        vector<int> xs, ys;
        for (auto& r : rooks) {
            xs.push_back(r[0]);
            ys.push_back(r[1]);
        }
        sort(xs.begin(), xs.end());
        sort(ys.begin(), ys.end());
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            ans += abs(xs[i] - i);
            ans += abs(ys[i] - i);
        }
        return ans;
    }
};
Go
import "sort"
func minMovesToPeacefulBoard(rooks [][]int) int {
    n := len(rooks)
    xs, ys := make([]int, n), make([]int, n)
    for i, r := range rooks {
        xs[i], ys[i] = r[0], r[1]
    }
    sort.Ints(xs)
    sort.Ints(ys)
    ans := 0
    for i := 0; i < n; i++ {
        ans += abs(xs[i]-i) + abs(ys[i]-i)
    }
    return ans
}
func abs(x int) int { if x < 0 { return -x }; return x }
Java
class Solution {
    public int minMovesToPeacefulBoard(int[][] rooks) {
        int n = rooks.length;
        int[] xs = new int[n], ys = new int[n];
        for (int i = 0; i < n; i++) {
            xs[i] = rooks[i][0];
            ys[i] = rooks[i][1];
        }
        Arrays.sort(xs);
        Arrays.sort(ys);
        int ans = 0;
        for (int i = 0; i < n; i++) {
            ans += Math.abs(xs[i] - i) + Math.abs(ys[i] - i);
        }
        return ans;
    }
}
Kotlin
class Solution {
    fun minMovesToPeacefulBoard(rooks: Array<IntArray>): Int {
        val n = rooks.size
        val xs = IntArray(n) { rooks[it][0] }
        val ys = IntArray(n) { rooks[it][1] }
        xs.sort()
        ys.sort()
        var ans = 0
        for (i in 0 until n) {
            ans += kotlin.math.abs(xs[i] - i) + kotlin.math.abs(ys[i] - i)
        }
        return ans
    }
}
Python
def min_moves_to_peaceful_board(rooks: list[list[int]]) -> int:
    n = len(rooks)
    xs = sorted(r[0] for r in rooks)
    ys = sorted(r[1] for r in rooks)
    return sum(abs(xs[i] - i) + abs(ys[i] - i) for i in range(n))
Rust
impl Solution {
    pub fn min_moves_to_peaceful_board(rooks: Vec<Vec<i32>>) -> i32 {
        let n = rooks.len();
        let mut xs: Vec<i32> = rooks.iter().map(|r| r[0]).collect();
        let mut ys: Vec<i32> = rooks.iter().map(|r| r[1]).collect();
        xs.sort(); ys.sort();
        let mut ans = 0;
        for i in 0..n {
            ans += (xs[i] - i as i32).abs() + (ys[i] - i as i32).abs();
        }
        ans
    }
}
TypeScript
class Solution {
    minMovesToPeacefulBoard(rooks: number[][]): number {
        const n = rooks.length;
        const xs = rooks.map(r => r[0]).sort((a, b) => a - b);
        const ys = rooks.map(r => r[1]).sort((a, b) => a - b);
        let ans = 0;
        for (let i = 0; i < n; i++) {
            ans += Math.abs(xs[i] - i) + Math.abs(ys[i] - i);
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n log n), where n is the number of rooks. Sorting dominates.
  • 🧺 Space complexity: O(n), for storing coordinates.

Comments