Minimum Moves to Move a Box to Their Target Location
HardUpdated: Aug 2, 2025
Practice on:
Problem
A storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.
The game is represented by an m x n grid of characters grid where each element is a wall, floor, or box.
Your task is to move the box 'B' to the target position 'T' under the following rules:
- The character
'S'represents the player. The player can move up, down, left, right ingridif it is a floor (empty cell). - The character
'.'represents the floor which means a free cell to walk. - The character
'#'represents the wall which means an obstacle (impossible to walk there). - There is only one box
'B'and one target cell'T'in thegrid. - The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a push.
- The player cannot walk through the box.
Return the minimum number ofpushes to move the box to the target. If there is no way to reach the target, return -1.
Examples
Example 1
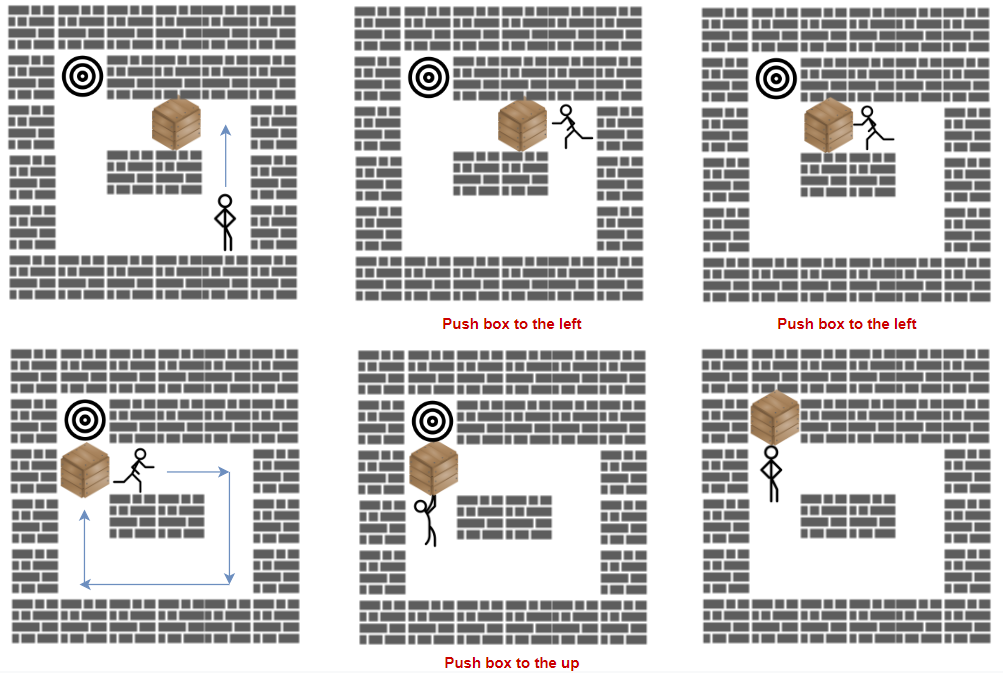
Input: grid = [["#","#","#","#","#","#"],
["#","T","#","#","#","#"],
["#",".",".","B",".","#"],
["#",".","#","#",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
Output: 3
Explanation: We return only the number of times the box is pushed.
Example 2
Input: grid = [["#","#","#","#","#","#"],
["#","T","#","#","#","#"],
["#",".",".","B",".","#"],
["#","#","#","#",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
Output: -1
Example 3
Input: grid = [["#","#","#","#","#","#"],
["#","T",".",".","#","#"],
["#",".","#","B",".","#"],
["#",".",".",".",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
Output: 5
Explanation: push the box down, left, left, up and up.
Constraints
m == grid.lengthn == grid[i].length1 <= m, n <= 20gridcontains only characters'.','#','S','T', or'B'.- There is only one character
'S','B', and'T'in thegrid.
Solution
Method 1 – BFS with State Encoding
Intuition
We need to find the minimum number of pushes to move the box to the target. Each state is defined by the positions of the box and the player. We use BFS to explore all possible states, prioritizing pushes, and avoid revisiting states.
Approach
- Parse the grid to find the initial positions of the box, player, and target.
- Use BFS to explore states: each state is
(box_x, box_y, player_x, player_y). - For each direction, check if the player can reach the position to push the box.
- If the box reaches the target, return the number of pushes.
- Use a set to avoid revisiting states.
- If no solution, return -1.
Code
C++
class Solution {
public:
int minPushBox(vector<vector<char>>& grid) {
int m = grid.size(), n = grid[0].size();
int bx, by, px, py, tx, ty;
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 'B') bx = i, by = j;
if (grid[i][j] == 'S') px = i, py = j;
if (grid[i][j] == 'T') tx = i, ty = j;
}
vector<vector<int>> dirs{{0,1},{0,-1},{1,0},{-1,0}};
auto canReach = [&](int sx, int sy, int ex, int ey, int bx, int by) {
vector<vector<bool>> vis(m, vector<bool>(n));
queue<pair<int,int>> q;
q.push({sx, sy});
vis[sx][sy] = true;
while (!q.empty()) {
auto [x, y] = q.front(); q.pop();
if (x == ex && y == ey) return true;
for (auto& d : dirs) {
int nx = x + d[0], ny = y + d[1];
if (nx >= 0 && nx < m && ny >= 0 && ny < n &&
!vis[nx][ny] && grid[nx][ny] != '#' &&
!(nx == bx && ny == by)) {
vis[nx][ny] = true;
q.push({nx, ny});
}
}
}
return false;
};
set<tuple<int,int,int,int>> vis;
queue<tuple<int,int,int,int,int>> q;
q.push({bx, by, px, py, 0});
vis.insert({bx, by, px, py});
while (!q.empty()) {
auto [bx, by, px, py, moves] = q.front(); q.pop();
if (bx == tx && by == ty) return moves;
for (auto& d : dirs) {
int nbx = bx + d[0], nby = by + d[1];
int ppx = bx - d[0], ppy = by - d[1];
if (nbx < 0 || nbx >= m || nby < 0 || nby >= n ||
grid[nbx][nby] == '#') continue;
if (ppx < 0 || ppx >= m || ppy < 0 || ppy >= n ||
grid[ppx][ppy] == '#') continue;
if (!canReach(px, py, ppx, ppy, bx, by)) continue;
if (vis.count({nbx, nby, bx, by})) continue;
vis.insert({nbx, nby, bx, by});
q.push({nbx, nby, bx, by, moves + 1});
}
}
return -1;
}
};
Go
func minPushBox(grid [][]byte) int {
m, n := len(grid), len(grid[0])
var bx, by, px, py, tx, ty int
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
switch grid[i][j] {
case 'B':
bx, by = i, j
case 'S':
px, py = i, j
case 'T':
tx, ty = i, j
}
}
}
dirs := [][]int{{0,1},{0,-1},{1,0},{-1,0}}
canReach := func(sx, sy, ex, ey, bx, by int) bool {
vis := make([][]bool, m)
for i := range vis { vis[i] = make([]bool, n) }
q := [][2]int{{sx, sy}}
vis[sx][sy] = true
for len(q) > 0 {
x, y := q[0][0], q[0][1]
q = q[1:]
if x == ex && y == ey { return true }
for _, d := range dirs {
nx, ny := x+d[0], y+d[1]
if nx >= 0 && nx < m && ny >= 0 && ny < n &&
!vis[nx][ny] && grid[nx][ny] != '#' &&
!(nx == bx && ny == by) {
vis[nx][ny] = true
q = append(q, [2]int{nx, ny})
}
}
}
return false
}
type state struct{ bx, by, px, py int }
vis := map[state]bool{}
q := []struct{ bx, by, px, py, moves int }{{bx, by, px, py, 0}}
vis[state{bx, by, px, py}] = true
for len(q) > 0 {
s := q[0]; q = q[1:]
if s.bx == tx && s.by == ty { return s.moves }
for _, d := range dirs {
nbx, nby := s.bx+d[0], s.by+d[1]
ppx, ppy := s.bx-d[0], s.by-d[1]
if nbx < 0 || nbx >= m || nby < 0 || nby >= n || grid[nbx][nby] == '#' { continue }
if ppx < 0 || ppx >= m || ppy < 0 || ppy >= n || grid[ppx][ppy] == '#' { continue }
if !canReach(s.px, s.py, ppx, ppy, s.bx, s.by) { continue }
ns := state{nbx, nby, s.bx, s.by}
if vis[ns] { continue }
vis[ns] = true
q = append(q, struct{ bx, by, px, py, moves int }{nbx, nby, s.bx, s.by, s.moves + 1})
}
}
return -1
}
Java
class Solution {
public int minPushBox(char[][] grid) {
int m = grid.length, n = grid[0].length;
int bx = 0, by = 0, px = 0, py = 0, tx = 0, ty = 0;
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 'B') { bx = i; by = j; }
if (grid[i][j] == 'S') { px = i; py = j; }
if (grid[i][j] == 'T') { tx = i; ty = j; }
}
int[][] dirs = {{0,1},{0,-1},{1,0},{-1,0}};
class State { int bx, by, px, py; State(int a, int b, int c, int d) { bx=a;by=b;px=c;py=d; } }
Set<String> vis = new HashSet<>();
Queue<int[]> q = new LinkedList<>();
q.offer(new int[]{bx, by, px, py, 0});
vis.add(bx + "," + by + "," + px + "," + py);
while (!q.isEmpty()) {
int[] s = q.poll();
if (s[0] == tx && s[1] == ty) return s[4];
for (int[] d : dirs) {
int nbx = s[0] + d[0], nby = s[1] + d[1];
int ppx = s[0] - d[0], ppy = s[1] - d[1];
if (nbx < 0 || nbx >= m || nby < 0 || nby >= n || grid[nbx][nby] == '#') continue;
if (ppx < 0 || ppx >= m || ppy < 0 || ppy >= n || grid[ppx][ppy] == '#') continue;
if (!canReach(grid, s[2], s[3], ppx, ppy, s[0], s[1])) continue;
String key = nbx + "," + nby + "," + s[0] + "," + s[1];
if (vis.contains(key)) continue;
vis.add(key);
q.offer(new int[]{nbx, nby, s[0], s[1], s[4] + 1});
}
}
return -1;
}
private boolean canReach(char[][] grid, int sx, int sy, int ex, int ey, int bx, int by) {
int m = grid.length, n = grid[0].length;
boolean[][] vis = new boolean[m][n];
Queue<int[]> q = new LinkedList<>();
q.offer(new int[]{sx, sy});
vis[sx][sy] = true;
int[][] dirs = {{0,1},{0,-1},{1,0},{-1,0}};
while (!q.isEmpty()) {
int[] s = q.poll();
if (s[0] == ex && s[1] == ey) return true;
for (int[] d : dirs) {
int nx = s[0] + d[0], ny = s[1] + d[1];
if (nx >= 0 && nx < m && ny >= 0 && ny < n &&
!vis[nx][ny] && grid[nx][ny] != '#' &&
!(nx == bx && ny == by)) {
vis[nx][ny] = true;
q.offer(new int[]{nx, ny});
}
}
}
return false;
}
}
Kotlin
class Solution {
fun minPushBox(grid: Array<CharArray>): Int {
val m = grid.size
val n = grid[0].size
var bx = 0; var by = 0; var px = 0; var py = 0; var tx = 0; var ty = 0
for (i in 0 until m)
for (j in 0 until n) {
when (grid[i][j]) {
'B' -> { bx = i; by = j }
'S' -> { px = i; py = j }
'T' -> { tx = i; ty = j }
}
}
val dirs = arrayOf(intArrayOf(0,1), intArrayOf(0,-1), intArrayOf(1,0), intArrayOf(-1,0))
data class State(val bx: Int, val by: Int, val px: Int, val py: Int)
val vis = mutableSetOf<State>()
val q = ArrayDeque<Pair<State, Int>>()
q.add(State(bx, by, px, py) to 0)
vis.add(State(bx, by, px, py))
fun canReach(sx: Int, sy: Int, ex: Int, ey: Int, bx: Int, by: Int): Boolean {
val vis2 = Array(m) { BooleanArray(n) }
val q2 = ArrayDeque<Pair<Int, Int>>()
q2.add(sx to sy)
vis2[sx][sy] = true
while (q2.isNotEmpty()) {
val (x, y) = q2.removeFirst()
if (x == ex && y == ey) return true
for (d in dirs) {
val nx = x + d[0]; val ny = y + d[1]
if (nx in 0 until m && ny in 0 until n &&
!vis2[nx][ny] && grid[nx][ny] != '#' &&
!(nx == bx && ny == by)) {
vis2[nx][ny] = true
q2.add(nx to ny)
}
}
}
return false
}
while (q.isNotEmpty()) {
val (state, moves) = q.removeFirst()
if (state.bx == tx && state.by == ty) return moves
for (d in dirs) {
val nbx = state.bx + d[0]; val nby = state.by + d[1]
val ppx = state.bx - d[0]; val ppy = state.by - d[1]
if (nbx !in 0 until m || nby !in 0 until n || grid[nbx][nby] == '#') continue
if (ppx !in 0 until m || ppy !in 0 until n || grid[ppx][ppy] == '#') continue
if (!canReach(state.px, state.py, ppx, ppy, state.bx, state.by)) continue
val newState = State(nbx, nby, state.bx, state.by)
if (newState in vis) continue
vis.add(newState)
q.add(newState to moves + 1)
}
}
return -1
}
}
Python
class Solution:
def minPushBox(self, grid: list[list[str]]) -> int:
from collections import deque
m, n = len(grid), len(grid[0])
bx = by = px = py = tx = ty = 0
for i in range(m):
for j in range(n):
if grid[i][j] == 'B': bx, by = i, j
if grid[i][j] == 'S': px, py = i, j
if grid[i][j] == 'T': tx, ty = i, j
dirs = [(0,1),(0,-1),(1,0),(-1,0)]
def can_reach(sx: int, sy: int, ex: int, ey: int, bx: int, by: int) -> bool:
vis = [[False]*n for _ in range(m)]
q = deque([(sx, sy)])
vis[sx][sy] = True
while q:
x, y = q.popleft()
if x == ex and y == ey: return True
for dx, dy in dirs:
nx, ny = x+dx, y+dy
if 0<=nx<m and 0<=ny<n and not vis[nx][ny] and grid[nx][ny]!='#' and (nx!=bx or ny!=by):
vis[nx][ny] = True
q.append((nx, ny))
return False
vis = set()
q = deque([(bx, by, px, py, 0)])
vis.add((bx, by, px, py))
while q:
bx, by, px, py, moves = q.popleft()
if bx == tx and by == ty: return moves
for dx, dy in dirs:
nbx, nby = bx+dx, by+dy
ppx, ppy = bx-dx, by-dy
if not (0<=nbx<m and 0<=nby<n and grid[nbx][nby]!='#'): continue
if not (0<=ppx<m and 0<=ppy<n and grid[ppx][ppy]!='#'): continue
if not can_reach(px, py, ppx, ppy, bx, by): continue
if (nbx, nby, bx, by) in vis: continue
vis.add((nbx, nby, bx, by))
q.append((nbx, nby, bx, by, moves+1))
return -1
Rust
use std::collections::{HashSet, VecDeque};
impl Solution {
pub fn min_push_box(grid: Vec<Vec<char>>) -> i32 {
let m = grid.len();
let n = grid[0].len();
let (mut bx, mut by, mut px, mut py, mut tx, mut ty) = (0,0,0,0,0,0);
for i in 0..m {
for j in 0..n {
match grid[i][j] {
'B' => { bx = i; by = j; }
'S' => { px = i; py = j; }
'T' => { tx = i; ty = j; }
_ => {}
}
}
}
let dirs = [(0,1),(0,-1),(1,0),(-1,0)];
let can_reach = |sx: usize, sy: usize, ex: usize, ey: usize, bx: usize, by: usize| -> bool {
let mut vis = vec![vec![false; n]; m];
let mut q = VecDeque::new();
q.push_back((sx, sy));
vis[sx][sy] = true;
while let Some((x, y)) = q.pop_front() {
if x == ex && y == ey { return true; }
for &(dx, dy) in &dirs {
let nx = x as isize + dx;
let ny = y as isize + dy;
if nx >= 0 && nx < m as isize && ny >= 0 && ny < n as isize {
let nx = nx as usize;
let ny = ny as usize;
if !vis[nx][ny] && grid[nx][ny] != '#' && !(nx == bx && ny == by) {
vis[nx][ny] = true;
q.push_back((nx, ny));
}
}
}
}
false
};
let mut vis = HashSet::new();
let mut q = VecDeque::new();
q.push_back((bx, by, px, py, 0));
vis.insert((bx, by, px, py));
while let Some((bx, by, px, py, moves)) = q.pop_front() {
if bx == tx && by == ty { return moves as i32; }
for &(dx, dy) in &dirs {
let nbx = bx as isize + dx;
let nby = by as isize + dy;
let ppx = bx as isize - dx;
let ppy = by as isize - dy;
if nbx < 0 || nbx >= m as isize || nby < 0 || nby >= n as isize || grid[nbx as usize][nby as usize] == '#' { continue; }
if ppx < 0 || ppx >= m as isize || ppy < 0 || ppy >= n as isize || grid[ppx as usize][ppy as usize] == '#' { continue; }
if !can_reach(px, py, ppx as usize, ppy as usize, bx, by) { continue; }
if vis.contains(&(nbx as usize, nby as usize, bx, by)) { continue; }
vis.insert((nbx as usize, nby as usize, bx, by));
q.push_back((nbx as usize, nby as usize, bx, by, moves+1));
}
}
-1
}
}
TypeScript
class Solution {
minPushBox(grid: string[][]): number {
const m = grid.length, n = grid[0].length;
let bx = 0, by = 0, px = 0, py = 0, tx = 0, ty = 0;
for (let i = 0; i < m; ++i)
for (let j = 0; j < n; ++j) {
if (grid[i][j] === 'B') { bx = i; by = j; }
if (grid[i][j] === 'S') { px = i; py = j; }
if (grid[i][j] === 'T') { tx = i; ty = j; }
}
const dirs = [[0,1],[0,-1],[1,0],[-1,0]];
function canReach(sx: number, sy: number, ex: number, ey: number, bx: number, by: number): boolean {
const vis = Array.from({length: m}, () => Array(n).fill(false));
const q: [number, number][] = [[sx, sy]];
vis[sx][sy] = true;
while (q.length) {
const [x, y] = q.shift()!;
if (x === ex && y === ey) return true;
for (const [dx, dy] of dirs) {
const nx = x + dx, ny = y + dy;
if (nx >= 0 && nx < m && ny >= 0 && ny < n &&
!vis[nx][ny] && grid[nx][ny] !== '#' &&
!(nx === bx && ny === by)) {
vis[nx][ny] = true;
q.push([nx, ny]);
}
}
}
return false;
}
const vis = new Set<string>();
const q: [number, number, number, number, number][] = [[bx, by, px, py, 0]];
vis.add(`${bx},${by},${px},${py}`);
while (q.length) {
const [bx, by, px, py, moves] = q.shift()!;
if (bx === tx && by === ty) return moves;
for (const [dx, dy] of dirs) {
const nbx = bx + dx, nby = by + dy;
const ppx = bx - dx, ppy = by - dy;
if (nbx < 0 || nbx >= m || nby < 0 || nby >= n || grid[nbx][nby] === '#') continue;
if (ppx < 0 || ppx >= m || ppy < 0 || ppy >= n || grid[ppx][ppy] === '#') continue;
if (!canReach(px, py, ppx, ppy, bx, by)) continue;
const key = `${nbx},${nby},${bx},${by}`;
if (vis.has(key)) continue;
vis.add(key);
q.push([nbx, nby, bx, by, moves+1]);
}
}
return -1;
}
}
Complexity
- ⏰ Time complexity:
O(mn * mn), as each state is a combination of box and player positions, and for each push, we may need to search the grid for player reachability. - 🧺 Space complexity:
O(mn * mn), for visited states and BFS queue.