Minimum Moves to Reach Target with Rotations
Problem
In an n*n grid, there is a snake that spans 2 cells and starts moving from the top left corner at (0, 0) and (0, 1). The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at (n-1, n-2) and (n-1, n-1).
In one move the snake can:
-
Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
-
Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
-
Rotate clockwise if it's in a horizontal position and the two cells under it are both empty. In that case the snake moves from
(r, c)and(r, c+1)to(r, c)and(r+1, c).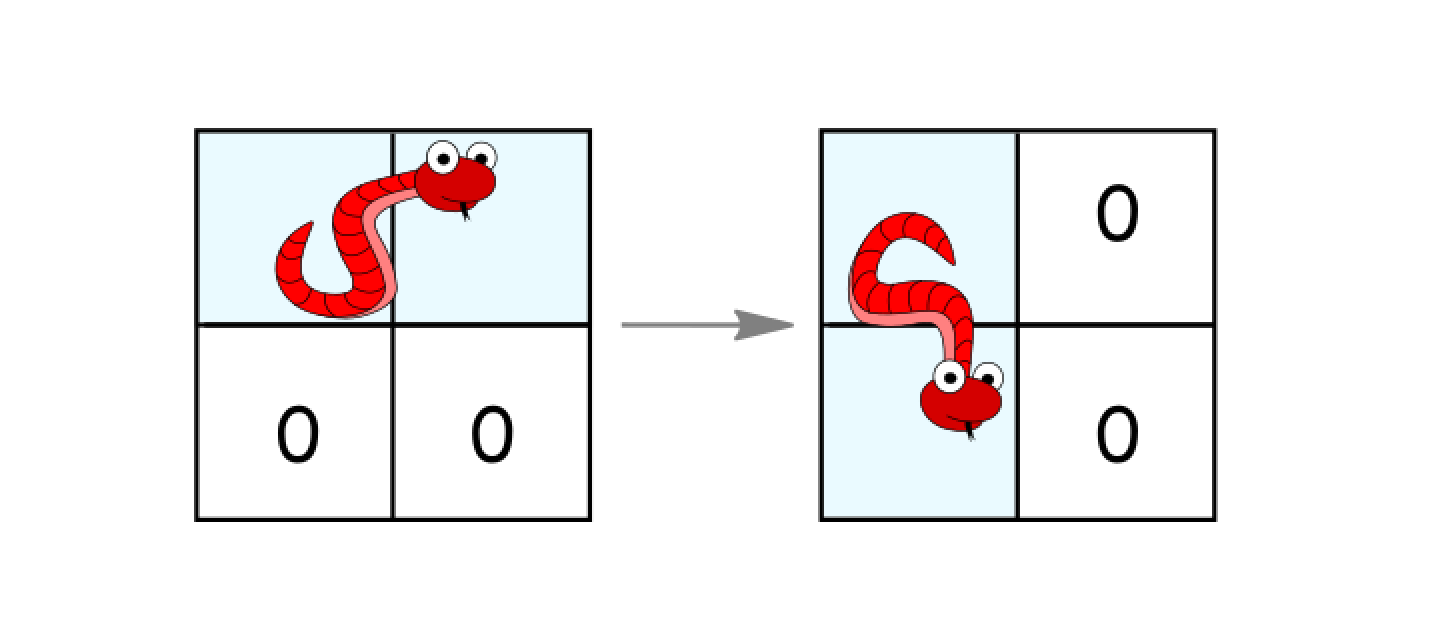
-
Rotate counterclockwise if it's in a vertical position and the two cells to its right are both empty. In that case the snake moves from
(r, c)and(r+1, c)to(r, c)and(r, c+1).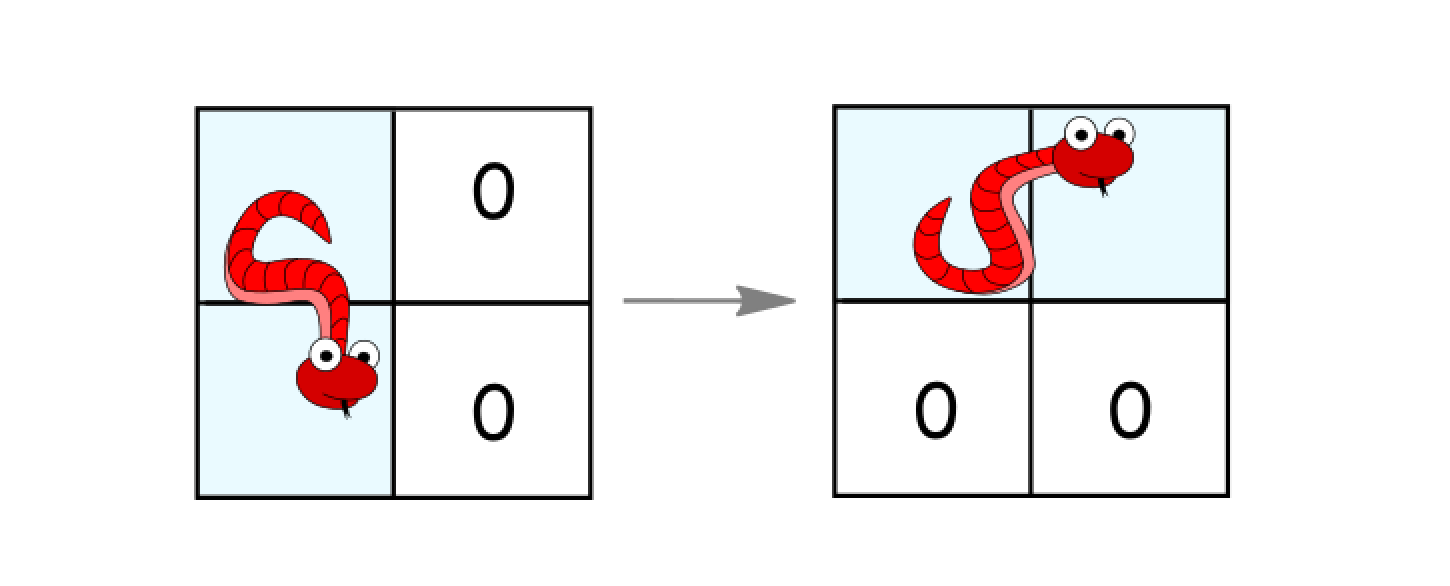
Return the minimum number of moves to reach the target.
If there is no way to reach the target, return -1.
Examples
Example 1
**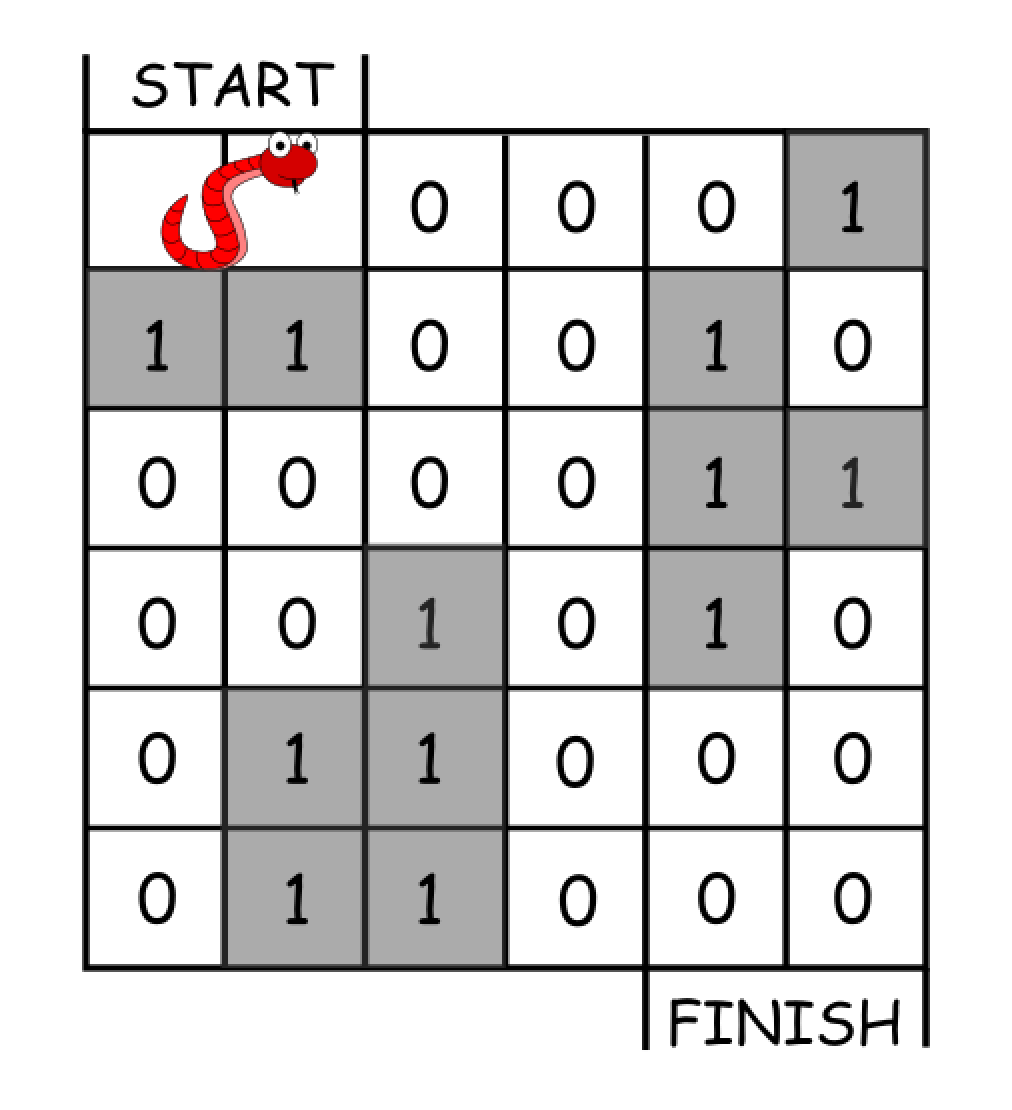**
Input: grid = [[0,0,0,0,0,1],
[1,1,0,0,1,0],
[0,0,0,0,1,1],
[0,0,1,0,1,0],
[0,1,1,0,0,0],
[0,1,1,0,0,0]]
Output: 11
Explanation: One possible solution is [right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down].
Example 2
Input: grid = [[0,0,1,1,1,1],
[0,0,0,0,1,1],
[1,1,0,0,0,1],
[1,1,1,0,0,1],
[1,1,1,0,0,1],
[1,1,1,0,0,0]]
Output: 9
Constraints
2 <= n <= 1000 <= grid[i][j] <= 1- It is guaranteed that the snake starts at empty cells.
Solution
Method 1 – BFS with State Encoding
Intuition
We model the snake's position as a state: the head's coordinates and orientation (horizontal or vertical). BFS explores all possible moves and rotations, ensuring the shortest path to the target is found.
Approach
- Use BFS to explore states:
(row, col, orientation)where orientation is 0 (horizontal) or 1 (vertical). - For each state, try moving right, down, and rotating if possible.
- Mark visited states to avoid cycles.
- Stop when the snake reaches the target position and orientation.
Code
C++
class Solution {
public:
int minMoves(vector<vector<int>>& grid) {
int n = grid.size();
queue<tuple<int,int,int,int>> q;
set<tuple<int,int,int>> vis;
q.push({0, 0, 0, 0}); // row, col, orientation, moves
vis.insert({0, 0, 0});
while (!q.empty()) {
auto [r, c, o, moves] = q.front(); q.pop();
if (r == n-1 && c == n-2 && o == 0) return moves;
// Move right
if (o == 0 && c+2 < n && grid[r][c+2] == 0 && !vis.count({r, c+1, 0})) {
vis.insert({r, c+1, 0});
q.push({r, c+1, 0, moves+1});
}
// Move down
if (o == 0 && r+1 < n && grid[r+1][c] == 0 && grid[r+1][c+1] == 0 && !vis.count({r+1, c, 0})) {
vis.insert({r+1, c, 0});
q.push({r+1, c, 0, moves+1});
}
// Rotate clockwise
if (o == 0 && r+1 < n && grid[r+1][c] == 0 && grid[r+1][c+1] == 0 && !vis.count({r, c, 1})) {
vis.insert({r, c, 1});
q.push({r, c, 1, moves+1});
}
// Move down (vertical)
if (o == 1 && r+2 < n && grid[r+2][c] == 0 && !vis.count({r+1, c, 1})) {
vis.insert({r+1, c, 1});
q.push({r+1, c, 1, moves+1});
}
// Move right (vertical)
if (o == 1 && c+1 < n && grid[r][c+1] == 0 && grid[r+1][c+1] == 0 && !vis.count({r, c+1, 1})) {
vis.insert({r, c+1, 1});
q.push({r, c+1, 1, moves+1});
}
// Rotate counterclockwise
if (o == 1 && c+1 < n && grid[r][c+1] == 0 && grid[r+1][c+1] == 0 && !vis.count({r, c, 0})) {
vis.insert({r, c, 0});
q.push({r, c, 0, moves+1});
}
}
return -1;
}
};
Go
func minMoves(grid [][]int) int {
n := len(grid)
type state struct{ r, c, o int }
vis := map[state]bool{}
q := []struct{ r, c, o, moves int }{{0, 0, 0, 0}}
vis[state{0, 0, 0}] = true
for len(q) > 0 {
s := q[0]; q = q[1:]
if s.r == n-1 && s.c == n-2 && s.o == 0 { return s.moves }
// Move right
if s.o == 0 && s.c+2 < n && grid[s.r][s.c+2] == 0 && !vis[state{s.r, s.c+1, 0}] {
vis[state{s.r, s.c+1, 0}] = true
q = append(q, struct{ r, c, o, moves int }{s.r, s.c+1, 0, s.moves+1})
}
// Move down
if s.o == 0 && s.r+1 < n && grid[s.r+1][s.c] == 0 && grid[s.r+1][s.c+1] == 0 && !vis[state{s.r+1, s.c, 0}] {
vis[state{s.r+1, s.c, 0}] = true
q = append(q, struct{ r, c, o, moves int }{s.r+1, s.c, 0, s.moves+1})
}
// Rotate clockwise
if s.o == 0 && s.r+1 < n && grid[s.r+1][s.c] == 0 && grid[s.r+1][s.c+1] == 0 && !vis[state{s.r, s.c, 1}] {
vis[state{s.r, s.c, 1}] = true
q = append(q, struct{ r, c, o, moves int }{s.r, s.c, 1, s.moves+1})
}
// Move down (vertical)
if s.o == 1 && s.r+2 < n && grid[s.r+2][s.c] == 0 && !vis[state{s.r+1, s.c, 1}] {
vis[state{s.r+1, s.c, 1}] = true
q = append(q, struct{ r, c, o, moves int }{s.r+1, s.c, 1, s.moves+1})
}
// Move right (vertical)
if s.o == 1 && s.c+1 < n && grid[s.r][s.c+1] == 0 && grid[s.r+1][s.c+1] == 0 && !vis[state{s.r, s.c+1, 1}] {
vis[state{s.r, s.c+1, 1}] = true
q = append(q, struct{ r, c, o, moves int }{s.r, s.c+1, 1, s.moves+1})
}
// Rotate counterclockwise
if s.o == 1 && s.c+1 < n && grid[s.r][s.c+1] == 0 && grid[s.r+1][s.c+1] == 0 && !vis[state{s.r, s.c, 0}] {
vis[state{s.r, s.c, 0}] = true
q = append(q, struct{ r, c, o, moves int }{s.r, s.c, 0, s.moves+1})
}
}
return -1
}
Java
class Solution {
public int minMoves(int[][] grid) {
int n = grid.length;
Queue<int[]> q = new LinkedList<>();
Set<String> vis = new HashSet<>();
q.offer(new int[]{0, 0, 0, 0});
vis.add("0,0,0");
while (!q.isEmpty()) {
int[] s = q.poll();
int r = s[0], c = s[1], o = s[2], moves = s[3];
if (r == n-1 && c == n-2 && o == 0) return moves;
// Move right
if (o == 0 && c+2 < n && grid[r][c+2] == 0 && !vis.contains((r)+","+(c+1)+",0")) {
vis.add((r)+","+(c+1)+",0");
q.offer(new int[]{r, c+1, 0, moves+1});
}
// Move down
if (o == 0 && r+1 < n && grid[r+1][c] == 0 && grid[r+1][c+1] == 0 && !vis.contains((r+1)+","+c+",0")) {
vis.add((r+1)+","+c+",0");
q.offer(new int[]{r+1, c, 0, moves+1});
}
// Rotate clockwise
if (o == 0 && r+1 < n && grid[r+1][c] == 0 && grid[r+1][c+1] == 0 && !vis.contains((r)+","+c+",1")) {
vis.add((r)+","+c+",1");
q.offer(new int[]{r, c, 1, moves+1});
}
// Move down (vertical)
if (o == 1 && r+2 < n && grid[r+2][c] == 0 && !vis.contains((r+1)+","+c+",1")) {
vis.add((r+1)+","+c+",1");
q.offer(new int[]{r+1, c, 1, moves+1});
}
// Move right (vertical)
if (o == 1 && c+1 < n && grid[r][c+1] == 0 && grid[r+1][c+1] == 0 && !vis.contains((r)+","+(c+1)+",1")) {
vis.add((r)+","+(c+1)+",1");
q.offer(new int[]{r, c+1, 1, moves+1});
}
// Rotate counterclockwise
if (o == 1 && c+1 < n && grid[r][c+1] == 0 && grid[r+1][c+1] == 0 && !vis.contains((r)+","+c+",0")) {
vis.add((r)+","+c+",0");
q.offer(new int[]{r, c, 0, moves+1});
}
}
return -1;
}
}
Kotlin
class Solution {
fun minMoves(grid: Array<IntArray>): Int {
val n = grid.size
val vis = mutableSetOf<Triple<Int, Int, Int>>()
val q = ArrayDeque<List<Int>>()
q.add(listOf(0, 0, 0, 0))
vis.add(Triple(0, 0, 0))
while (q.isNotEmpty()) {
val (r, c, o, moves) = q.removeFirst()
if (r == n-1 && c == n-2 && o == 0) return moves
// Move right
if (o == 0 && c+2 < n && grid[r][c+2] == 0 && !vis.contains(Triple(r, c+1, 0))) {
vis.add(Triple(r, c+1, 0))
q.add(listOf(r, c+1, 0, moves+1))
}
// Move down
if (o == 0 && r+1 < n && grid[r+1][c] == 0 && grid[r+1][c+1] == 0 && !vis.contains(Triple(r+1, c, 0))) {
vis.add(Triple(r+1, c, 0))
q.add(listOf(r+1, c, 0, moves+1))
}
// Rotate clockwise
if (o == 0 && r+1 < n && grid[r+1][c] == 0 && grid[r+1][c+1] == 0 && !vis.contains(Triple(r, c, 1))) {
vis.add(Triple(r, c, 1))
q.add(listOf(r, c, 1, moves+1))
}
// Move down (vertical)
if (o == 1 && r+2 < n && grid[r+2][c] == 0 && !vis.contains(Triple(r+1, c, 1))) {
vis.add(Triple(r+1, c, 1))
q.add(listOf(r+1, c, 1, moves+1))
}
// Move right (vertical)
if (o == 1 && c+1 < n && grid[r][c+1] == 0 && grid[r+1][c+1] == 0 && !vis.contains(Triple(r, c+1, 1))) {
vis.add(Triple(r, c+1, 1))
q.add(listOf(r, c+1, 1, moves+1))
}
// Rotate counterclockwise
if (o == 1 && c+1 < n && grid[r][c+1] == 0 && grid[r+1][c+1] == 0 && !vis.contains(Triple(r, c, 0))) {
vis.add(Triple(r, c, 0))
q.add(listOf(r, c, 0, moves+1))
}
}
return -1
}
}
Python
class Solution:
def minMoves(self, grid: list[list[int]]) -> int:
from collections import deque
n: int = len(grid)
vis: set = set()
q = deque([(0, 0, 0, 0)])
vis.add((0, 0, 0))
while q:
r, c, o, moves = q.popleft()
if r == n-1 and c == n-2 and o == 0:
return moves
# Move right
if o == 0 and c+2 < n and grid[r][c+2] == 0 and (r, c+1, 0) not in vis:
vis.add((r, c+1, 0))
q.append((r, c+1, 0, moves+1))
# Move down
if o == 0 and r+1 < n and grid[r+1][c] == 0 and grid[r+1][c+1] == 0 and (r+1, c, 0) not in vis:
vis.add((r+1, c, 0))
q.append((r+1, c, 0, moves+1))
# Rotate clockwise
if o == 0 and r+1 < n and grid[r+1][c] == 0 and grid[r+1][c+1] == 0 and (r, c, 1) not in vis:
vis.add((r, c, 1))
q.append((r, c, 1, moves+1))
# Move down (vertical)
if o == 1 and r+2 < n and grid[r+2][c] == 0 and (r+1, c, 1) not in vis:
vis.add((r+1, c, 1))
q.append((r+1, c, 1, moves+1))
# Move right (vertical)
if o == 1 and c+1 < n and grid[r][c+1] == 0 and grid[r+1][c+1] == 0 and (r, c+1, 1) not in vis:
vis.add((r, c+1, 1))
q.append((r, c+1, 1, moves+1))
# Rotate counterclockwise
if o == 1 and c+1 < n and grid[r][c+1] == 0 and grid[r+1][c+1] == 0 and (r, c, 0) not in vis:
vis.add((r, c, 0))
q.append((r, c, 0, moves+1))
return -1
Rust
use std::collections::{HashSet, VecDeque};
impl Solution {
pub fn min_moves(grid: Vec<Vec<i32>>) -> i32 {
let n = grid.len();
let mut vis = HashSet::new();
let mut q = VecDeque::new();
q.push_back((0, 0, 0, 0));
vis.insert((0, 0, 0));
while let Some((r, c, o, moves)) = q.pop_front() {
if r == n-1 && c == n-2 && o == 0 {
return moves;
}
// Move right
if o == 0 && c+2 < n && grid[r][c+2] == 0 && !vis.contains(&(r, c+1, 0)) {
vis.insert((r, c+1, 0));
q.push_back((r, c+1, 0, moves+1));
}
// Move down
if o == 0 && r+1 < n && grid[r+1][c] == 0 && grid[r+1][c+1] == 0 && !vis.contains(&(r+1, c, 0)) {
vis.insert((r+1, c, 0));
q.push_back((r+1, c, 0, moves+1));
}
// Rotate clockwise
if o == 0 && r+1 < n && grid[r+1][c] == 0 && grid[r+1][c+1] == 0 && !vis.contains(&(r, c, 1)) {
vis.insert((r, c, 1));
q.push_back((r, c, 1, moves+1));
}
// Move down (vertical)
if o == 1 && r+2 < n && grid[r+2][c] == 0 && !vis.contains(&(r+1, c, 1)) {
vis.insert((r+1, c, 1));
q.push_back((r+1, c, 1, moves+1));
}
// Move right (vertical)
if o == 1 && c+1 < n && grid[r][c+1] == 0 && grid[r+1][c+1] == 0 && !vis.contains(&(r, c+1, 1)) {
vis.insert((r, c+1, 1));
q.push_back((r, c+1, 1, moves+1));
}
// Rotate counterclockwise
if o == 1 && c+1 < n && grid[r][c+1] == 0 && grid[r+1][c+1] == 0 && !vis.contains(&(r, c, 0)) {
vis.insert((r, c, 0));
q.push_back((r, c, 0, moves+1));
}
}
-1
}
}
TypeScript
class Solution {
minMoves(grid: number[][]): number {
const n = grid.length;
const vis = new Set<string>();
const q: [number, number, number, number][] = [[0, 0, 0, 0]];
vis.add(`0,0,0`);
while (q.length) {
const [r, c, o, moves] = q.shift()!;
if (r === n-1 && c === n-2 && o === 0) return moves;
// Move right
if (o === 0 && c+2 < n && grid[r][c+2] === 0 && !vis.has(`${r},${c+1},0`)) {
vis.add(`${r},${c+1},0`);
q.push([r, c+1, 0, moves+1]);
}
// Move down
if (o === 0 && r+1 < n && grid[r+1][c] === 0 && grid[r+1][c+1] === 0 && !vis.has(`${r+1},${c},0`)) {
vis.add(`${r+1},${c},0`);
q.push([r+1, c, 0, moves+1]);
}
// Rotate clockwise
if (o === 0 && r+1 < n && grid[r+1][c] === 0 && grid[r+1][c+1] === 0 && !vis.has(`${r},${c},1`)) {
vis.add(`${r},${c},1`);
q.push([r, c, 1, moves+1]);
}
// Move down (vertical)
if (o === 1 && r+2 < n && grid[r+2][c] === 0 && !vis.has(`${r+1},${c},1`)) {
vis.add(`${r+1},${c},1`);
q.push([r+1, c, 1, moves+1]);
}
// Move right (vertical)
if (o === 1 && c+1 < n && grid[r][c+1] === 0 && grid[r+1][c+1] === 0 && !vis.has(`${r},${c+1},1`)) {
vis.add(`${r},${c+1},1`);
q.push([r, c+1, 1, moves+1]);
}
// Rotate counterclockwise
if (o === 1 && c+1 < n && grid[r][c+1] === 0 && grid[r+1][c+1] === 0 && !vis.has(`${r},${c},0`)) {
vis.add(`${r},${c},0`);
q.push([r, c, 0, moves+1]);
}
}
return -1;
}
}
Complexity
- ⏰ Time complexity:
O(n^2), as each state is visited at most once and there are up to2*n*nstates. - 🧺 Space complexity:
O(n^2), for the visited set and BFS queue.