Problems

You are given a binary string s. You are allowed to perform two types of operations on the string in any sequence:

  • Type-1: Remove the character at the start of the string s and append it to the end of the string.
  • Type-2: Pick any character in s and flip its value, i.e., if its value is '0' it becomes '1' and vice-versa.

Return the minimum number of type-2 operations you need to perform such that s becomes alternating.

The string is called alternating if no two adjacent characters are equal.

  • For example, the strings "010" and "1010" are alternating, while the string "0100" is not.

Examples

Example 1

1
2
3
4

Input: s = "111000"
Output: 2
Explanation: Use the first operation two times to make s = "100011".
Then, use the second operation on the third and sixth elements to make s = "10 _1_ 01 _0_ ".

Example 2

1
2
3

Input: s = "010"
Output: 0
Explanation : The string is already alternating.

Example 3

1
2
3

Input: s = "1110"
Output: 1
Explanation : Use the second operation on the second element to make s = "1 _0_ 10".

Constraints

  • 1 <= s.length <= 10^5
  • s[i] is either '0' or '1'.

Solution

Method 1 - Brute Force

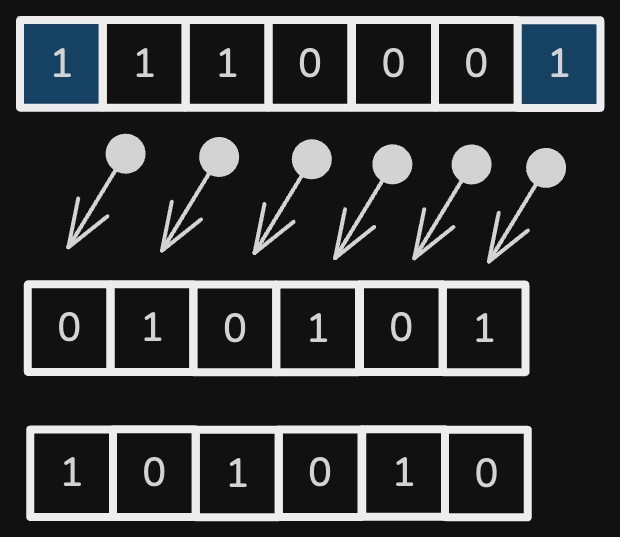
Lets take a string "111000". The target state can be S1 - "010101" OR S2 - "101010". Now if we are allowed to just second operation i.e. Type 2, then number of flips to get to S1 OR S2 will be O(n). But we are also allowed operation Type 1, where we take prefix and append to the end of string.

Now the brute force can be we take input string, perform T2 operation, check updated string is S1 OR S2.

Method 2 - Sliding Window with Alternating Patterns

Intuition

Since we can rotate the string any number of times, we can try all possible rotations. For each rotation, we count the minimum flips needed to make the string alternating (either starting with ‘0’ or ‘1’). We use a sliding window to efficiently check all rotations.

Approach

  • For the 1st operation T1, we can simply do s += s to append the whole string to the end.
  • then we make two different string with the same length by 01 and 10 alternative. for example: s = 11100
    • s = 1110011100
    • s1= 1010101010
    • s2= 0101010101
  • finally, use sliding window（size n）to compare s to both s1 and s2.
  • why we can double s to fullfil the first operation, let’s look at the same example s = 11100:`
    • double s: 1110011100
    • size n window: |11100|11100 ==> 1|11001|1100 ==> 11|10011|100 and so on, when we move one step of the sliding window, it is the same to append 1 more element from beginning.

Here is the summary:

  1. Concatenate the string to itself to simulate all rotations.
  2. For each window of length n, count flips needed for both patterns (‘0101…’ and ‘1010…’).
  3. Track the minimum flips over all windows.
  4. Return the minimum flips found.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
public:
    int minFlips(string s) {
        int n = s.size();
        string ss = s + s;
        int ans = n;
        int flip0 = 0, flip1 = 0;
        for (int i = 0; i < 2*n; ++i) {
            char c = ss[i];
            if (c != (i%2 ? '1' : '0')) flip0++;
            if (c != (i%2 ? '0' : '1')) flip1++;
            if (i >= n) {
                char out = ss[i-n];
                if (out != ((i-n)%2 ? '1' : '0')) flip0--;
                if (out != ((i-n)%2 ? '0' : '1')) flip1--;
            }
            if (i >= n-1) ans = min(ans, min(flip0, flip1));
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

func minFlips(s string) int {
    n := len(s)
    ss := s + s
    ans, flip0, flip1 := n, 0, 0
    for i := 0; i < 2*n; i++ {
        c := ss[i]
        if c != byte('0'+i%2) { flip0++ }
        if c != byte('1'-i%2) { flip1++ }
        if i >= n {
            out := ss[i-n]
            if out != byte('0'+(i-n)%2) { flip0-- }
            if out != byte('1'-(i-n)%2) { flip1-- }
        }
        if i >= n-1 {
            if flip0 < ans { ans = flip0 }
            if flip1 < ans { ans = flip1 }
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
    public int minFlips(String s) {
        int n = s.length();
        String ss = s + s;
        int ans = n, flip0 = 0, flip1 = 0;
        for (int i = 0; i < 2*n; ++i) {
            char c = ss.charAt(i);
            if (c != (i%2==0 ? '0' : '1')) flip0++;
            if (c != (i%2==0 ? '1' : '0')) flip1++;
            if (i >= n) {
                char out = ss.charAt(i-n);
                if (out != ((i-n)%2==0 ? '0' : '1')) flip0--;
                if (out != ((i-n)%2==0 ? '1' : '0')) flip1--;
            }
            if (i >= n-1) ans = Math.min(ans, Math.min(flip0, flip1));
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
    fun minFlips(s: String): Int {
        val n = s.length
        val ss = s + s
        var ans = n
        var flip0 = 0
        var flip1 = 0
        for (i in 0 until 2*n) {
            val c = ss[i]
            if (c != if (i%2==0) '0' else '1') flip0++
            if (c != if (i%2==0) '1' else '0') flip1++
            if (i >= n) {
                val out = ss[i-n]
                if (out != if ((i-n)%2==0) '0' else '1') flip0--
                if (out != if ((i-n)%2==0) '1' else '0') flip1--
            }
            if (i >= n-1) ans = minOf(ans, minOf(flip0, flip1))
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution:
    def minFlips(self, s: str) -> int:
        n: int = len(s)
        ss: str = s + s
        ans: int = n
        flip0: int = 0
        flip1: int = 0
        for i in range(2*n):
            c = ss[i]
            if c != ('0' if i%2==0 else '1'):
                flip0 += 1
            if c != ('1' if i%2==0 else '0'):
                flip1 += 1
            if i >= n:
                out = ss[i-n]
                if out != ('0' if (i-n)%2==0 else '1'):
                    flip0 -= 1
                if out != ('1' if (i-n)%2==0 else '0'):
                    flip1 -= 1
            if i >= n-1:
                ans = min(ans, flip0, flip1)
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

impl Solution {
    pub fn min_flips(s: String) -> i32 {
        let n = s.len();
        let ss = s.clone() + &s;
        let mut ans = n as i32;
        let mut flip0 = 0;
        let mut flip1 = 0;
        let bytes = ss.as_bytes();
        for i in 0..2*n {
            let c = bytes[i];
            if c != if i%2==0 { b'0' } else { b'1' } { flip0 += 1; }
            if c != if i%2==0 { b'1' } else { b'0' } { flip1 += 1; }
            if i >= n {
                let out = bytes[i-n];
                if out != if (i-n)%2==0 { b'0' } else { b'1' } { flip0 -= 1; }
                if out != if (i-n)%2==0 { b'1' } else { b'0' } { flip1 -= 1; }
            }
            if i >= n-1 {
                ans = ans.min(flip0).min(flip1);
            }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
    minFlips(s: string): number {
        const n = s.length;
        const ss = s + s;
        let ans = n, flip0 = 0, flip1 = 0;
        for (let i = 0; i < 2*n; ++i) {
            const c = ss[i];
            if (c !== (i%2 === 0 ? '0' : '1')) flip0++;
            if (c !== (i%2 === 0 ? '1' : '0')) flip1++;
            if (i >= n) {
                const out = ss[i-n];
                if (out !== ((i-n)%2 === 0 ? '0' : '1')) flip0--;
                if (out !== ((i-n)%2 === 0 ? '1' : '0')) flip1--;
            }
            if (i >= n-1) ans = Math.min(ans, flip0, flip1);
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n), as we process each character at most twice.
  • 🧺 Space complexity: O(n), for the concatenated string.