problemmediumalgorithmsleetcode-2268leetcode 2268leetcode2268

Minimum Number of Keypresses

MediumUpdated: Jul 26, 2025
Practice on:
LeetCode

Problem

You have a keypad with 9 buttons, numbered from 1 to 9, each mapped to lowercase English letters. You can choose which characters each button is matched to as long as:

  • All 26 lowercase English letters are mapped to.
  • Each character is mapped to by exactly 1 button.
  • Each button maps to at most 3 characters.

To type the first character matched to a button, you press the button once. To type the second character, you press the button twice, and so on.

Given a string s, return _theminimum number of keypresses needed to type _s using your keypad.

Note that the characters mapped to by each button, and the order they are mapped in cannot be changed.

Examples

Example 1:

Input: s = "apple"
Output: 5
Explanation: One optimal way to setup your keypad is shown above.
Type 'a' by pressing button 1 once.
Type 'p' by pressing button 6 once.
Type 'p' by pressing button 6 once.
Type 'l' by pressing button 5 once.
Type 'e' by pressing button 3 once.
A total of 5 button presses are needed, so return 5.

Example 2: 

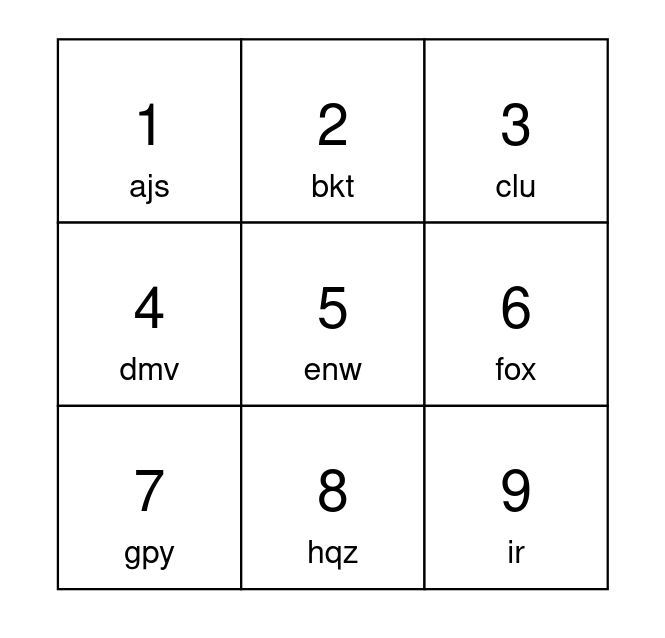
Input: s = "abcdefghijkl"
Output: 15
Explanation: One optimal way to setup your keypad is shown above.
The letters 'a' to 'i' can each be typed by pressing a button once.
Type 'j' by pressing button 1 twice.
Type 'k' by pressing button 2 twice.
Type 'l' by pressing button 3 twice.
A total of 15 button presses are needed, so return 15.

Constraints:

  • 1 <= s.length <= 10^5
  • s consists of lowercase English letters.

Solution

Method 1 – Greedy Frequency Assignment

Intuition

Assign the most frequent letters to the first position of each button, next most frequent to the second, and so on. This minimizes total keypresses.

Approach

  1. Count frequency of each letter in s.
  2. Sort frequencies descending.
  3. For the top 9, each press costs 1; next 9 cost 2; last 8 cost 3.
  4. Sum up total keypresses.

Code

C++
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
    int minimumKeypresses(string s) {
        vector<int> freq(26, 0);
        for (char c : s) freq[c-'a']++;
        sort(freq.rbegin(), freq.rend());
        int ans = 0;
        for (int i = 0; i < 26; ++i) {
            ans += freq[i] * (i/9 + 1);
        }
        return ans;
    }
};
Go
func minimumKeypresses(s string) int {
    freq := make([]int, 26)
    for _, c := range s { freq[c-'a']++ }
    sort.Slice(freq, func(i, j int) bool { return freq[i] > freq[j] })
    ans := 0
    for i := 0; i < 26; i++ {
        ans += freq[i] * (i/9 + 1)
    }
    return ans
}
Java
import java.util.*;
class Solution {
    public int minimumKeypresses(String s) {
        int[] freq = new int[26];
        for (char c : s.toCharArray()) freq[c-'a']++;
        Arrays.sort(freq);
        int ans = 0;
        for (int i = 0; i < 26; ++i) {
            ans += freq[25-i] * (i/9 + 1);
        }
        return ans;
    }
}
Kotlin
class Solution {
    fun minimumKeypresses(s: String): Int {
        val freq = IntArray(26)
        for (c in s) freq[c-'a']++
        freq.sortDescending()
        var ans = 0
        for (i in 0 until 26) {
            ans += freq[i] * (i/9 + 1)
        }
        return ans
    }
}
Python
class Solution:
    def minimumKeypresses(self, s: str) -> int:
        from collections import Counter
        freq = sorted(Counter(s).values(), reverse=True)
        freq += [0] * (26 - len(freq))
        return sum(freq[i] * (i//9 + 1) for i in range(26))
Rust
impl Solution {
    pub fn minimum_keypresses(s: String) -> i32 {
        let mut freq = vec![0; 26];
        for c in s.chars() { freq[c as usize - 'a' as usize] += 1; }
        freq.sort_by(|a, b| b.cmp(a));
        let mut ans = 0;
        for i in 0..26 { ans += freq[i] * (i/9 + 1); }
        ans
    }
}
TypeScript
class Solution {
    minimumKeypresses(s: string): number {
        const freq = Array(26).fill(0);
        for (const c of s) freq[c.charCodeAt(0) - 97]++;
        freq.sort((a, b) => b - a);
        let ans = 0;
        for (let i = 0; i < 26; ++i) ans += freq[i] * (Math.floor(i/9) + 1);
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n + 26 log 26) — n = length of s.
  • 🧺 Space complexity: O(1) — only 26 counters.

Comments