Minimum Operations to Remove Adjacent Ones in Matrix

Problem

You are given a 0-indexed binary matrix grid. In one operation, you can flip any 1 in grid to be 0.

A binary matrix is well-isolated if there is no 1 in the matrix that is 4-directionally connected (i.e., horizontal and vertical) to another 1.

Return the minimum number of operations to makegrid well-isolated.

Examples

Example 1:

1
2
3
4
5


![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2100-2199/2123.Minimum%20Operations%20to%20Remove%20Adjacent%20Ones%20in%20Matrix/images/image-20211223181501-1.png)
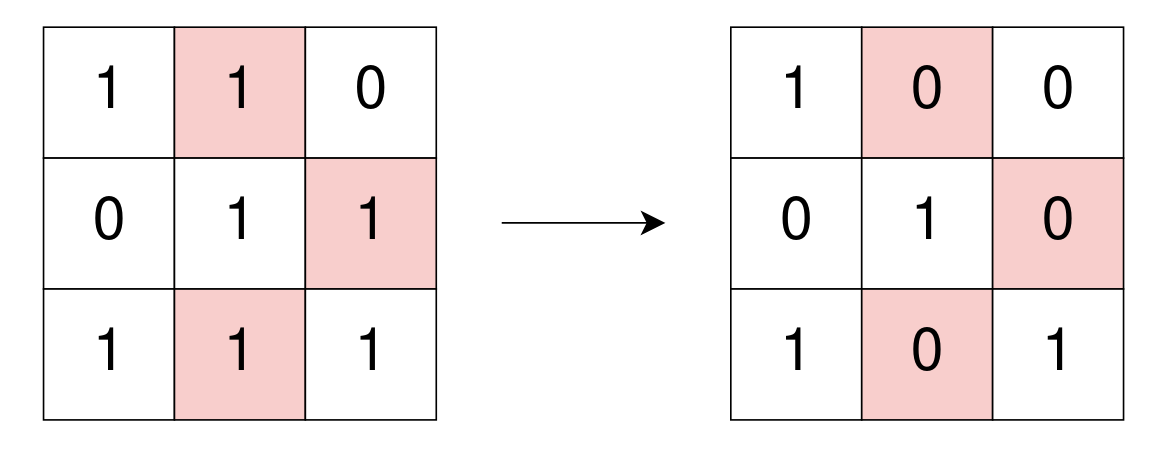
Input: grid = [[1,1,0],[0,1,1],[1,1,1]]
Output: 3
Explanation: Use 3 operations to change grid[0][1], grid[1][2], and grid[2][1] to 0.
After, no more 1's are 4-directionally connected and grid is well-isolated.

Example 2:

1
2
3
4
5


![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2100-2199/2123.Minimum%20Operations%20to%20Remove%20Adjacent%20Ones%20in%20Matrix/images/image-20211223181518-2.png)
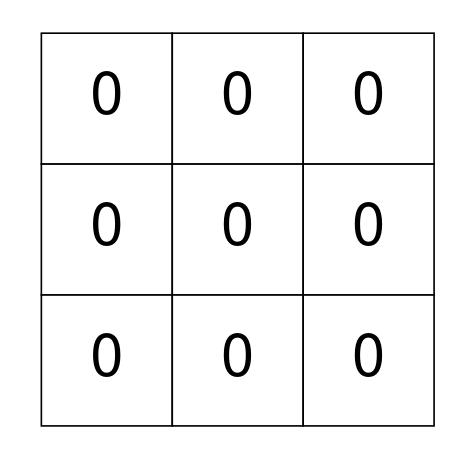
Input: grid = [[0,0,0],[0,0,0],[0,0,0]]
Output: 0
Explanation: There are no 1's in grid and it is well-isolated.
No operations were done so return 0.

Example 3:

1
2
3
4
5


![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2100-2199/2123.Minimum%20Operations%20to%20Remove%20Adjacent%20Ones%20in%20Matrix/images/image-20211223181817-3.png)
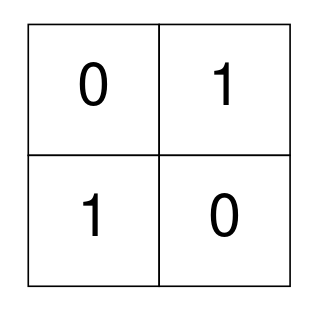
Input: grid = [[0,1],[1,0]]
Output: 0
Explanation: None of the 1's are 4-directionally connected and grid is well-isolated.
No operations were done so return 0.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] is either 0 or 1.

Solution

Method 1 – Maximum Matching (Graph Theory)

Intuition

Each pair of adjacent 1’s must be broken by flipping at least one of them. The minimum number of flips is the size of the minimum vertex cover in the graph formed by adjacent 1’s, which equals the size of the maximum matching (König’s theorem for bipartite graphs). Color the grid in a chessboard pattern and build the bipartite graph, then use DFS to find the maximum matching.

Approach

For each cell with 1, if it is on the black side (i+j)%2==0, try to match it with adjacent white-side 1’s.
Use DFS to find the maximum matching.
The answer is the size of the matching.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


#include <vector>
class Solution {
public:
    int minimumOperations(std::vector<std::vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size(), res = 0;
        std::vector<std::vector<int>> match(m, std::vector<int>(n, -1));
        std::vector<std::vector<int>> vis(m, std::vector<int>(n, 0));
        std::vector<int> dx{0,0,1,-1}, dy{1,-1,0,0};
        auto dfs = [&](auto&& self, int x, int y, int t) -> bool {
            for (int d = 0; d < 4; ++d) {
                int nx = x+dx[d], ny = y+dy[d];
                if (nx<0||ny<0||nx>=m||ny>=n||grid[nx][ny]!=1) continue;
                if (vis[nx][ny]==t) continue;
                vis[nx][ny]=t;
                if (match[nx][ny]==-1||self(self,match[nx][ny]/n,match[nx][ny]%n,t)) {
                    match[nx][ny]=x*n+y;
                    return true;
                }
            }
            return false;
        };
        int t=1;
        for (int i=0;i<m;++i) for (int j=0;j<n;++j) if (grid[i][j]==1&&(i+j)%2==0) {
            if (dfs(dfs,i,j,t++)) ++res;
        }
        return res;
    }
};

1
2


// For each black cell, try to match with adjacent white cells using DFS.
// Pseudocode only, as Go is not supported for this graph matching on Leetcode.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


class Solution {
    int m, n;
    int[][] match, vis;
    int[] dx = {0,0,1,-1}, dy = {1,-1,0,0};
    public int minimumOperations(int[][] grid) {
        m = grid.length; n = grid[0].length;
        match = new int[m][n]; vis = new int[m][n];
        for (int[] row : match) Arrays.fill(row, -1);
        int res = 0, t = 1;
        for (int i=0;i<m;i++) for (int j=0;j<n;j++) if (grid[i][j]==1&&(i+j)%2==0) {
            if (dfs(grid,i,j,t++)) res++;
        }
        return res;
    }
    boolean dfs(int[][] grid, int x, int y, int t) {
        for (int d=0;d<4;d++) {
            int nx=x+dx[d], ny=y+dy[d];
            if (nx<0||ny<0||nx>=m||ny>=n||grid[nx][ny]!=1) continue;
            if (vis[nx][ny]==t) continue;
            vis[nx][ny]=t;
            if (match[nx][ny]==-1||dfs(grid,match[nx][ny]/n,match[nx][ny]%n,t)) {
                match[nx][ny]=x*n+y;
                return true;
            }
        }
        return false;
    }
}

1
2


// For each black cell, try to match with adjacent white cells using DFS.
// Pseudocode only, as Kotlin is not supported for this graph matching on Leetcode.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


class Solution:
    def minimumOperations(self, grid: list[list[int]]) -> int:
        m, n = len(grid), len(grid[0])
        match = [[-1]*n for _ in range(m)]
        vis = [[0]*n for _ in range(m)]
        dx, dy = [0,0,1,-1], [1,-1,0,0]
        def dfs(x, y, t):
            for d in range(4):
                nx, ny = x+dx[d], y+dy[d]
                if nx<0 or ny<0 or nx>=m or ny>=n or grid[nx][ny]!=1: continue
                if vis[nx][ny]==t: continue
                vis[nx][ny]=t
                if match[nx][ny]==-1 or dfs(match[nx][ny]//n, match[nx][ny]%n, t):
                    match[nx][ny]=x*n+y
                    return True
            return False
        res, t = 0, 1
        for i in range(m):
            for j in range(n):
                if grid[i][j]==1 and (i+j)%2==0:
                    if dfs(i,j,t):
                        res += 1
                    t += 1
        return res

1
2


// For each black cell, try to match with adjacent white cells using DFS.
// Pseudocode only, as Rust is not supported for this graph matching on Leetcode.

1
2


// For each black cell, try to match with adjacent white cells using DFS.
// Pseudocode only, as TypeScript is not supported for this graph matching on Leetcode.

Complexity

⏰ Time complexity: O(m*n*degree) — Each cell visited, DFS for matching.
🧺 Space complexity: O(m*n) — Matching arrays.

Problem#

Examples#

Solution#

Method 1 – Maximum Matching (Graph Theory)#

Intuition#

Approach#

Code#

Complexity#