Minimum Operations to Write the Letter Y on a Grid
MediumUpdated: Aug 2, 2025
Practice on:
Problem
You are given a 0-indexed n x n grid where n is odd, and grid[r][c]
is 0, 1, or 2.
We say that a cell belongs to the Letter Y if it belongs to one of the following:
- The diagonal starting at the top-left cell and ending at the center cell of the grid.
- The diagonal starting at the top-right cell and ending at the center cell of the grid.
- The vertical line starting at the center cell and ending at the bottom border of the grid.
The Letter Y is written on the grid if and only if:
- All values at cells belonging to the Y are equal.
- All values at cells not belonging to the Y are equal.
- The values at cells belonging to the Y are different from the values at cells not belonging to the Y.
Return theminimum number of operations needed to write the letter Y on the grid given that in one operation you can change the value at any cell to
0 , 1 , or 2 .
Examples
Example 1
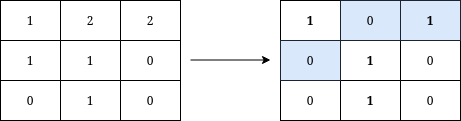
Input: grid = [[1,2,2],[1,1,0],[0,1,0]]
Output: 3
Explanation: We can write Y on the grid by applying the changes highlighted in blue in the image above. After the operations, all cells that belong to Y, denoted in bold, have the same value of 1 while those that do not belong to Y are equal to 0.
It can be shown that 3 is the minimum number of operations needed to write Y on the grid.
Example 2
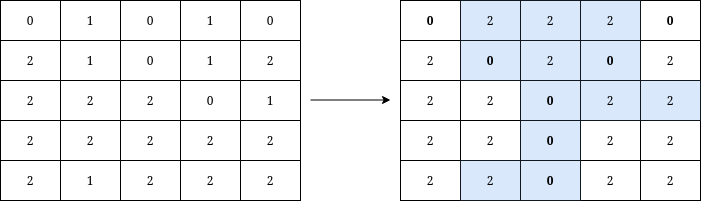
Input: grid = [[0,1,0,1,0],[2,1,0,1,2],[2,2,2,0,1],[2,2,2,2,2],[2,1,2,2,2]]
Output: 12
Explanation: We can write Y on the grid by applying the changes highlighted in blue in the image above. After the operations, all cells that belong to Y, denoted in bold, have the same value of 0 while those that do not belong to Y are equal to 2.
It can be shown that 12 is the minimum number of operations needed to write Y on the grid.
Constraints
3 <= n <= 49n == grid.length == grid[i].length0 <= grid[i][j] <= 2nis odd.
Solution
Method 1 – Counting and Brute Force
Intuition
For each possible value for Y and non-Y cells (must be different), count the number of changes needed to make all Y cells the same and all non-Y cells the same. Try all possible value pairs (0,1), (0,2), (1,0), (1,2), (2,0), (2,1).
Approach
- Identify all Y cells (two diagonals to center, vertical from center down).
- For each possible (y_val, non_y_val) with y_val != non_y_val:
- Count changes needed for Y cells to y_val.
- Count changes needed for non-Y cells to non_y_val.
- Track minimum total changes.
- Return the minimum.
Code
C++
#include <vector>
#include <algorithm>
class Solution {
public:
int minimumOperations(std::vector<std::vector<int>>& grid) {
int n = grid.size(), res = n*n;
std::vector<std::vector<bool>> isY(n, std::vector<bool>(n, false));
int c = n/2;
for (int i = 0; i < n; ++i) isY[i][i] = isY[i][n-1-i] = true;
for (int i = c; i < n; ++i) isY[i][c] = true;
for (int y_val = 0; y_val <= 2; ++y_val) {
for (int non_y_val = 0; non_y_val <= 2; ++non_y_val) {
if (y_val == non_y_val) continue;
int changes = 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (isY[i][j] && grid[i][j] != y_val) changes++;
if (!isY[i][j] && grid[i][j] != non_y_val) changes++;
}
}
res = std::min(res, changes);
}
}
return res;
}
};
Go
func minimumOperations(grid [][]int) int {
n := len(grid)
c := n/2
isY := make([][]bool, n)
for i := range isY { isY[i] = make([]bool, n) }
for i := 0; i < n; i++ { isY[i][i], isY[i][n-1-i] = true, true }
for i := c; i < n; i++ { isY[i][c] = true }
res := n*n
for yVal := 0; yVal <= 2; yVal++ {
for nonYVal := 0; nonYVal <= 2; nonYVal++ {
if yVal == nonYVal { continue }
changes := 0
for i := 0; i < n; i++ {
for j := 0; j < n; j++ {
if isY[i][j] && grid[i][j] != yVal { changes++ }
if !isY[i][j] && grid[i][j] != nonYVal { changes++ }
}
}
if changes < res { res = changes }
}
}
return res
}
Java
class Solution {
public int minimumOperations(int[][] grid) {
int n = grid.length, c = n/2, res = n*n;
boolean[][] isY = new boolean[n][n];
for (int i = 0; i < n; ++i) isY[i][i] = isY[i][n-1-i] = true;
for (int i = c; i < n; ++i) isY[i][c] = true;
for (int yVal = 0; yVal <= 2; ++yVal) {
for (int nonYVal = 0; nonYVal <= 2; ++nonYVal) {
if (yVal == nonYVal) continue;
int changes = 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (isY[i][j] && grid[i][j] != yVal) changes++;
if (!isY[i][j] && grid[i][j] != nonYVal) changes++;
}
}
res = Math.min(res, changes);
}
}
return res;
}
}
Kotlin
class Solution {
fun minimumOperations(grid: Array<IntArray>): Int {
val n = grid.size
val c = n/2
val isY = Array(n) { BooleanArray(n) }
for (i in 0 until n) { isY[i][i] = true; isY[i][n-1-i] = true }
for (i in c until n) isY[i][c] = true
var res = n*n
for (yVal in 0..2) {
for (nonYVal in 0..2) {
if (yVal == nonYVal) continue
var changes = 0
for (i in 0 until n) {
for (j in 0 until n) {
if (isY[i][j] && grid[i][j] != yVal) changes++
if (!isY[i][j] && grid[i][j] != nonYVal) changes++
}
}
res = minOf(res, changes)
}
}
return res
}
}
Python
class Solution:
def minimumOperations(self, grid: list[list[int]]) -> int:
n = len(grid)
c = n//2
isY = [[False]*n for _ in range(n)]
for i in range(n):
isY[i][i] = isY[i][n-1-i] = True
for i in range(c, n):
isY[i][c] = True
res = n*n
for y_val in range(3):
for non_y_val in range(3):
if y_val == non_y_val: continue
changes = 0
for i in range(n):
for j in range(n):
if isY[i][j] and grid[i][j] != y_val:
changes += 1
if not isY[i][j] and grid[i][j] != non_y_val:
changes += 1
res = min(res, changes)
return res
Rust
impl Solution {
pub fn minimum_operations(grid: Vec<Vec<i32>>) -> i32 {
let n = grid.len();
let c = n/2;
let mut is_y = vec![vec![false;n];n];
for i in 0..n { is_y[i][i]=true; is_y[i][n-1-i]=true; }
for i in c..n { is_y[i][c]=true; }
let mut res = (n*n) as i32;
for y_val in 0..3 {
for non_y_val in 0..3 {
if y_val==non_y_val { continue; }
let mut changes = 0;
for i in 0..n {
for j in 0..n {
if is_y[i][j] && grid[i][j]!=y_val { changes+=1; }
if !is_y[i][j] && grid[i][j]!=non_y_val { changes+=1; }
}
}
res = res.min(changes);
}
}
res
}
}
TypeScript
class Solution {
minimumOperations(grid: number[][]): number {
const n = grid.length, c = Math.floor(n/2);
const isY = Array.from({length:n},()=>Array(n).fill(false));
for (let i=0;i<n;i++) { isY[i][i]=true; isY[i][n-1-i]=true; }
for (let i=c;i<n;i++) isY[i][c]=true;
let res = n*n;
for (let yVal=0; yVal<=2; yVal++) {
for (let nonYVal=0; nonYVal<=2; nonYVal++) {
if (yVal===nonYVal) continue;
let changes = 0;
for (let i=0;i<n;i++) {
for (let j=0;j<n;j++) {
if (isY[i][j] && grid[i][j]!==yVal) changes++;
if (!isY[i][j] && grid[i][j]!==nonYVal) changes++;
}
}
res = Math.min(res, changes);
}
}
return res;
}
}
Complexity
- ⏰ Time complexity:
O(n^2)— Try all value pairs, scan grid. - 🧺 Space complexity:
O(n^2)— Y mask.