problemmediumalgorithmsleetcode-2492leetcode 2492leetcode2492

Minimum Score of a Path Between Two Cities

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given a positive integer n representing n cities numbered from 1 to n. You are also given a 2D array roads where roads[i] = [ai, bi, distancei] indicates that there is a bidirectional road between cities ai and bi with a distance equal to distancei. The cities graph is not necessarily connected.

The score of a path between two cities is defined as the minimum distance of a road in this path.

Return _theminimum possible score of a path between cities _1 andn.

Note :

  • A path is a sequence of roads between two cities.
  • It is allowed for a path to contain the same road multiple times, and you can visit cities 1 and n multiple times along the path.
  • The test cases are generated such that there is at least one path between 1 and n.

Examples

Example 1


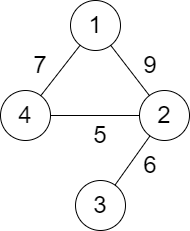
![](https://assets.leetcode.com/uploads/2022/10/12/graph11.png)

Input: n = 4, roads = [[1,2,9],[2,3,6],[2,4,5],[1,4,7]]
Output: 5
Explanation: The path from city 1 to 4 with the minimum score is: 1 -> 2 -> 4. The score of this path is min(9,5) = 5.
It can be shown that no other path has less score.

Example 2


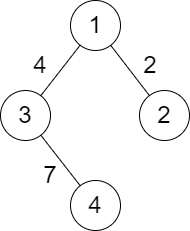
![](https://assets.leetcode.com/uploads/2022/10/12/graph22.png)

Input: n = 4, roads = [[1,2,2],[1,3,4],[3,4,7]]
Output: 2
Explanation: The path from city 1 to 4 with the minimum score is: 1 -> 2 -> 1 -> 3 -> 4. The score of this path is min(2,2,4,7) = 2.

Constraints

  • 2 <= n <= 10^5
  • 1 <= roads.length <= 10^5
  • roads[i].length == 3
  • 1 <= ai, bi <= n
  • ai != bi
  • 1 <= distancei <= 10^4
  • There are no repeated edges.
  • There is at least one path between 1 and n.

Solution

Method 1 – BFS/DFS Connected Component

Intuition

Since you can revisit cities and roads, the minimum score is the smallest edge in the connected component containing city 1. Traverse all reachable cities from 1 and track the minimum edge.

Approach

  1. Build adjacency list.
  2. BFS/DFS from city 1, mark visited.
  3. For each edge traversed, track the minimum distance.
  4. Return the minimum found.

Code

C++
#include <vector>
#include <queue>
#include <algorithm>
class Solution {
public:
    int minScore(int n, vector<vector<int>>& roads) {
        vector<vector<pair<int,int>>> g(n+1);
        for (auto& r : roads) {
            g[r[0]].push_back({r[1],r[2]});
            g[r[1]].push_back({r[0],r[2]});
        }
        vector<bool> vis(n+1);
        int res = 1e4+1;
        queue<int> q; q.push(1); vis[1]=true;
        while (!q.empty()) {
            int u = q.front(); q.pop();
            for (auto& [v,d] : g[u]) {
                res = min(res,d);
                if (!vis[v]) { vis[v]=true; q.push(v); }
            }
        }
        return res;
    }
};
Go
func minScore(n int, roads [][]int) int {
    g := make([][][2]int, n+1)
    for _, r := range roads {
        g[r[0]] = append(g[r[0]], [2]int{r[1],r[2]})
        g[r[1]] = append(g[r[1]], [2]int{r[0],r[2]})
    }
    vis := make([]bool, n+1)
    res := 10001
    q := []int{1}; vis[1]=true
    for len(q)>0 {
        u := q[0]; q = q[1:]
        for _, e := range g[u] {
            v,d := e[0],e[1]
            if d < res { res = d }
            if !vis[v] { vis[v]=true; q = append(q,v) }
        }
    }
    return res
}
Java
import java.util.*;
class Solution {
    public int minScore(int n, int[][] roads) {
        List<int[]>[] g = new List[n+1];
        for (int i = 1; i <= n; i++) g[i] = new ArrayList<>();
        for (int[] r : roads) {
            g[r[0]].add(new int[]{r[1],r[2]});
            g[r[1]].add(new int[]{r[0],r[2]});
        }
        boolean[] vis = new boolean[n+1];
        int res = 10001;
        Queue<Integer> q = new LinkedList<>(); q.add(1); vis[1]=true;
        while (!q.isEmpty()) {
            int u = q.poll();
            for (int[] e : g[u]) {
                int v = e[0], d = e[1];
                res = Math.min(res,d);
                if (!vis[v]) { vis[v]=true; q.add(v); }
            }
        }
        return res;
    }
}
Kotlin
class Solution {
    fun minScore(n: Int, roads: Array<IntArray>): Int {
        val g = Array(n+1){mutableListOf<Pair<Int,Int>>()} 
        for (r in roads) {
            g[r[0]].add(r[1] to r[2])
            g[r[1]].add(r[0] to r[2])
        }
        val vis = BooleanArray(n+1)
        var res = 10001
        val q = ArrayDeque<Int>()
        q.add(1); vis[1]=true
        while (q.isNotEmpty()) {
            val u = q.removeFirst()
            for ((v,d) in g[u]) {
                res = minOf(res,d)
                if (!vis[v]) { vis[v]=true; q.add(v) }
            }
        }
        return res
    }
}
Python
from collections import deque,defaultdict
class Solution:
    def minScore(self, n: int, roads: list[list[int]]) -> int:
        g = defaultdict(list)
        for a,b,d in roads:
            g[a].append((b,d))
            g[b].append((a,d))
        vis = [False]*(n+1)
        res = 10001
        q = deque([1]); vis[1]=True
        while q:
            u = q.popleft()
            for v,d in g[u]:
                res = min(res,d)
                if not vis[v]: vis[v]=True; q.append(v)
        return res
Rust
use std::collections::{VecDeque,HashMap};
impl Solution {
    pub fn min_score(n: i32, roads: Vec<Vec<i32>>) -> i32 {
        let mut g: HashMap<i32, Vec<(i32,i32)>> = HashMap::new();
        for r in &roads {
            g.entry(r[0]).or_default().push((r[1],r[2]));
            g.entry(r[1]).or_default().push((r[0],r[2]));
        }
        let mut vis = vec![false; n as usize+1];
        let mut res = 10001;
        let mut q = VecDeque::new(); q.push_back(1); vis[1]=true;
        while let Some(u) = q.pop_front() {
            if let Some(adj) = g.get(&u) {
                for &(v,d) in adj {
                    res = res.min(d);
                    if !vis[v as usize] { vis[v as usize]=true; q.push_back(v); }
                }
            }
        }
        res
    }
}
TypeScript
class Solution {
    minScore(n: number, roads: number[][]): number {
        const g: Map<number, [number,number][]> = new Map();
        for (const [a,b,d] of roads) {
            if (!g.has(a)) g.set(a,[]);
            if (!g.has(b)) g.set(b,[]);
            g.get(a)!.push([b,d]);
            g.get(b)!.push([a,d]);
        }
        const vis = Array(n+1).fill(false);
        let res = 10001;
        const q = [1]; vis[1]=true;
        while (q.length) {
            const u = q.shift()!;
            for (const [v,d] of g.get(u)!) {
                res = Math.min(res,d);
                if (!vis[v]) { vis[v]=true; q.push(v); }
            }
        }
        return res;
    }
}

Complexity

  • ⏰ Time complexity: O(n + m) — Traverse all roads and cities.
  • 🧺 Space complexity: O(n + m) — For adjacency list and visited array.

Comments