Minimum Sideway Jumps

Problem

There is a 3 lane road of length n that consists of n + 1 points labeled from 0 to n. A frog starts at point 0 in the second lane**** and wants to jump to point n. However, there could be obstacles along the way.

You are given an array obstacles of length n + 1 where each obstacles[i] (ranging from 0 to 3) describes an obstacle on the lane obstacles[i] at point i. If obstacles[i] == 0, there are no obstacles at point i. There will be at most one obstacle in the 3 lanes at each point.

For example, if obstacles[2] == 1, then there is an obstacle on lane 1 at point 2.

The frog can only travel from point i to point i + 1 on the same lane if there is not an obstacle on the lane at point i + 1. To avoid obstacles, the frog can also perform a side jump to jump to another lane (even if they are not adjacent) at the same point if there is no obstacle on the new lane.

For example, the frog can jump from lane 3 at point 3 to lane 1 at point 3.

Return theminimum number of side jumps the frog needs to reach any lane at point n starting from lane 2 at point 0.

Note: There will be no obstacles on points 0 and n.

Examples

Example 1

1
2
3
4
5
6
7



![](https://assets.leetcode.com/uploads/2021/03/25/ic234-q3-ex1.png)

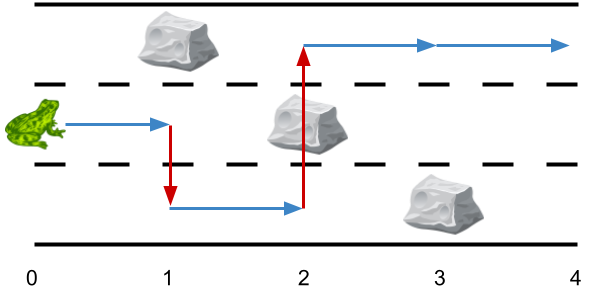
Input: obstacles = [0,1,2,3,0]
Output: 2 
Explanation: The optimal solution is shown by the arrows above. There are 2 side jumps (red arrows).
Note that the frog can jump over obstacles only when making side jumps (as shown at point 2).

Example 2

1
2
3
4
5
6



![](https://assets.leetcode.com/uploads/2021/03/25/ic234-q3-ex2.png)

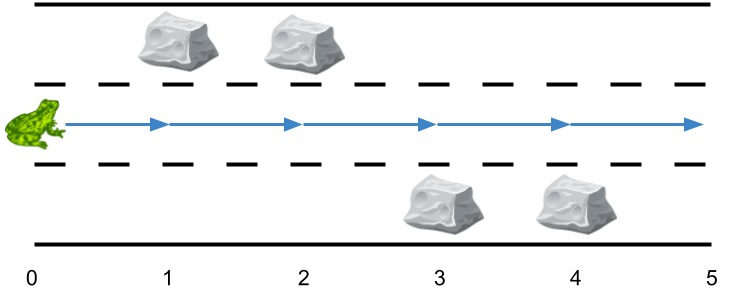
Input: obstacles = [0,1,1,3,3,0]
Output: 0
Explanation: There are no obstacles on lane 2. No side jumps are required.

Example 3

1
2
3
4
5
6



![](https://assets.leetcode.com/uploads/2021/03/25/ic234-q3-ex3.png)

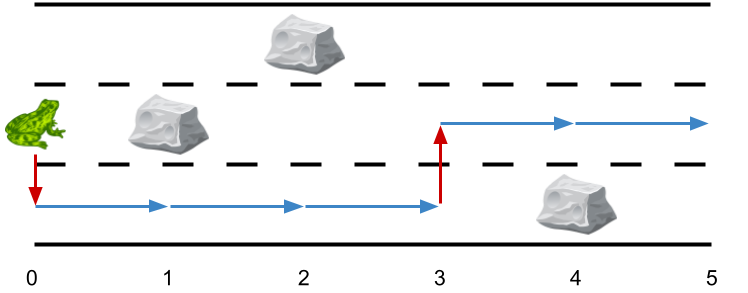
Input: obstacles = [0,2,1,0,3,0]
Output: 2
Explanation: The optimal solution is shown by the arrows above. There are 2 side jumps.

Constraints

obstacles.length == n + 1
1 <= n <= 5 * 10^5
0 <= obstacles[i] <= 3
obstacles[0] == obstacles[n] == 0

Solution

Method 1 – Dynamic Programming (Greedy Lane Tracking)

Intuition

We use DP to track the minimum side jumps needed to reach each lane at each point. At each step, we can move forward in the same lane (if no obstacle) or side jump to another lane (if no obstacle there). Start at lane 2, point 0.

Approach

Let dp[lane] be the minimum jumps to reach current point in lane. For each point, update dp for lanes without obstacles. For side jumps, take min of other lanes + 1. Initialize dp = [1,0,1] at point 0 (since frog starts at lane 2).

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


#include <vector>
#include <algorithm>
class Solution {
public:
    int minSideJumps(vector<int>& obstacles) {
        int n = obstacles.size();
        vector<int> dp = {1,0,1};
        for (int i = 1; i < n; ++i) {
            for (int lane = 0; lane < 3; ++lane)
                if (obstacles[i] == lane+1) dp[lane] = 1e6;
            for (int lane = 0; lane < 3; ++lane)
                if (obstacles[i] != lane+1)
                    dp[lane] = std::min(dp[lane], std::min(dp[(lane+1)%3], dp[(lane+2)%3])+1);
        }
        return std::min({dp[0],dp[1],dp[2]});
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


func minSideJumps(obstacles []int) int {
    dp := [3]int{1,0,1}
    for i := 1; i < len(obstacles); i++ {
        for lane := 0; lane < 3; lane++ {
            if obstacles[i] == lane+1 { dp[lane] = 1e6 }
        }
        for lane := 0; lane < 3; lane++ {
            if obstacles[i] != lane+1 {
                a, b := dp[(lane+1)%3], dp[(lane+2)%3]
                if a < b { b = a }
                if dp[lane] > b+1 { dp[lane] = b+1 }
            }
        }
    }
    res := dp[0]
    if dp[1] < res { res = dp[1] }
    if dp[2] < res { res = dp[2] }
    return res
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


class Solution {
    public int minSideJumps(int[] obstacles) {
        int[] dp = {1,0,1};
        int n = obstacles.length;
        for (int i = 1; i < n; i++) {
            for (int lane = 0; lane < 3; lane++)
                if (obstacles[i] == lane+1) dp[lane] = 1000000;
            for (int lane = 0; lane < 3; lane++)
                if (obstacles[i] != lane+1)
                    dp[lane] = Math.min(dp[lane], Math.min(dp[(lane+1)%3], dp[(lane+2)%3])+1);
        }
        return Math.min(dp[0], Math.min(dp[1], dp[2]));
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


class Solution {
    fun minSideJumps(obstacles: IntArray): Int {
        val dp = intArrayOf(1,0,1)
        for (i in 1 until obstacles.size) {
            for (lane in 0..2)
                if (obstacles[i] == lane+1) dp[lane] = 1000000
            for (lane in 0..2)
                if (obstacles[i] != lane+1)
                    dp[lane] = minOf(dp[lane], minOf(dp[(lane+1)%3], dp[(lane+2)%3])+1)
        }
        return minOf(dp[0], dp[1], dp[2])
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


class Solution:
    def minSideJumps(self, obstacles: list[int]) -> int:
        dp = [1,0,1]
        for i in range(1, len(obstacles)):
            for lane in range(3):
                if obstacles[i] == lane+1:
                    dp[lane] = 10**6
            for lane in range(3):
                if obstacles[i] != lane+1:
                    dp[lane] = min(dp[lane], min(dp[(lane+1)%3], dp[(lane+2)%3])+1)
        return min(dp)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


impl Solution {
    pub fn min_side_jumps(obstacles: Vec<i32>) -> i32 {
        let mut dp = [1,0,1];
        for i in 1..obstacles.len() {
            for lane in 0..3 {
                if obstacles[i] == lane as i32 + 1 { dp[lane] = 1_000_000; }
            }
            for lane in 0..3 {
                if obstacles[i] != lane as i32 + 1 {
                    let a = dp[(lane+1)%3];
                    let b = dp[(lane+2)%3];
                    dp[lane] = dp[lane].min(a.min(b)+1);
                }
            }
        }
        *dp.iter().min().unwrap()
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


class Solution {
    minSideJumps(obstacles: number[]): number {
        let dp = [1,0,1];
        for (let i = 1; i < obstacles.length; i++) {
            for (let lane = 0; lane < 3; lane++)
                if (obstacles[i] === lane+1) dp[lane] = 1e6;
            for (let lane = 0; lane < 3; lane++)
                if (obstacles[i] !== lane+1)
                    dp[lane] = Math.min(dp[lane], Math.min(dp[(lane+1)%3], dp[(lane+2)%3])+1);
        }
        return Math.min(...dp);
    }
}

Complexity

⏰ Time complexity: O(n) — One pass through obstacles.
🧺 Space complexity: O(1) — Only a few variables.

Problem#

Examples#

Example 1#

Example 2#

Example 3#

Constraints#

Solution#

Method 1 – Dynamic Programming (Greedy Lane Tracking)#

Intuition#

Approach#

Code#

Complexity#