Problem

Given an n x n binary grid, in one step you can choose two adjacent rows of the grid and swap them.

A grid is said to be valid if all the cells above the main diagonal are zeros.

Return the minimum number of steps needed to make the grid valid, or -1 if the grid cannot be valid.

The main diagonal of a grid is the diagonal that starts at cell (1, 1) and ends at cell (n, n).

Examples

Example 1

1
2
3
4
5


![](https://assets.leetcode.com/uploads/2020/07/28/fw.jpg)

Input: grid = [[0,0,1],[1,1,0],[1,0,0]]
Output: 3

Example 2

1
2
3
4
5
6


![](https://assets.leetcode.com/uploads/2020/07/16/e2.jpg)

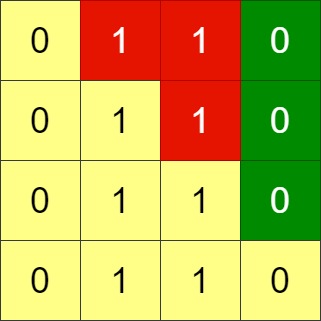
Input: grid = [[0,1,1,0],[0,1,1,0],[0,1,1,0],[0,1,1,0]]
Output: -1
Explanation: All rows are similar, swaps have no effect on the grid.

Example 3

1
2
3
4
5


![](https://assets.leetcode.com/uploads/2020/07/16/e3.jpg)

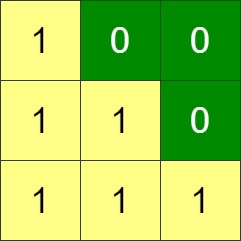
Input: grid = [[1,0,0],[1,1,0],[1,1,1]]
Output: 0

Constraints

  • n == grid.length == grid[i].length
  • 1 <= n <= 200
  • grid[i][j] is either 0 or 1

Solution

Method 1 – Greedy Row Swapping

Intuition

For each row i, we need at least n-i-1 trailing zeros (zeros to the right of the diagonal) to make the grid valid. We can greedily find the nearest row below with enough trailing zeros and swap it up, counting the swaps. If no such row exists, it’s impossible.

Approach

  1. For each row, count the number of trailing zeros.
  2. For each row i, find the first row j ≥ i with at least n-i-1 trailing zeros.
  3. Swap row j up to position i, counting the swaps.
  4. If no such row exists, return -1.
  5. Return the total swaps.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
public:
    int minSwaps(vector<vector<int>>& grid) {
        int n = grid.size(), ans = 0;
        vector<int> zeros(n);
        for (int i = 0; i < n; ++i) {
            int cnt = 0;
            for (int j = n-1; j >= 0 && grid[i][j] == 0; --j) cnt++;
            zeros[i] = cnt;
        }
        for (int i = 0; i < n; ++i) {
            int need = n-i-1, j = i;
            while (j < n && zeros[j] < need) ++j;
            if (j == n) return -1;
            while (j > i) { swap(zeros[j], zeros[j-1]); ans++; j--; }
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

func minSwaps(grid [][]int) int {
    n := len(grid)
    zeros := make([]int, n)
    for i := 0; i < n; i++ {
        cnt := 0
        for j := n-1; j >= 0 && grid[i][j] == 0; j-- { cnt++ }
        zeros[i] = cnt
    }
    ans := 0
    for i := 0; i < n; i++ {
        need, j := n-i-1, i
        for ; j < n && zeros[j] < need; j++ {}
        if j == n { return -1 }
        for ; j > i; j-- { zeros[j], zeros[j-1] = zeros[j-1], zeros[j]; ans++ }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

class Solution {
    public int minSwaps(int[][] grid) {
        int n = grid.length, ans = 0;
        int[] zeros = new int[n];
        for (int i = 0; i < n; i++) {
            int cnt = 0;
            for (int j = n-1; j >= 0 && grid[i][j] == 0; j--) cnt++;
            zeros[i] = cnt;
        }
        for (int i = 0; i < n; i++) {
            int need = n-i-1, j = i;
            while (j < n && zeros[j] < need) j++;
            if (j == n) return -1;
            while (j > i) { int tmp=zeros[j]; zeros[j]=zeros[j-1]; zeros[j-1]=tmp; ans++; j--; }
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
    fun minSwaps(grid: Array<IntArray>): Int {
        val n = grid.size
        val zeros = IntArray(n)
        for (i in 0 until n) {
            var cnt = 0
            for (j in n-1 downTo 0) {
                if (grid[i][j] == 0) cnt++ else break
            }
            zeros[i] = cnt
        }
        var ans = 0
        for (i in 0 until n) {
            val need = n-i-1
            var j = i
            while (j < n && zeros[j] < need) j++
            if (j == n) return -1
            while (j > i) {
                zeros[j] = zeros[j-1].also { zeros[j-1] = zeros[j] }
                ans++
                j--
            }
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution:
    def minSwaps(self, grid: list[list[int]]) -> int:
        n = len(grid)
        zeros = [0]*n
        for i in range(n):
            cnt = 0
            for j in range(n-1, -1, -1):
                if grid[i][j] == 0: cnt += 1
                else: break
            zeros[i] = cnt
        ans = 0
        for i in range(n):
            need = n-i-1
            j = i
            while j < n and zeros[j] < need: j += 1
            if j == n: return -1
            while j > i:
                zeros[j], zeros[j-1] = zeros[j-1], zeros[j]
                ans += 1
                j -= 1
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

impl Solution {
    pub fn min_swaps(grid: Vec<Vec<i32>>) -> i32 {
        let n = grid.len();
        let mut zeros = vec![0; n];
        for i in 0..n {
            let mut cnt = 0;
            for j in (0..n).rev() {
                if grid[i][j] == 0 { cnt += 1; } else { break; }
            }
            zeros[i] = cnt;
        }
        let mut ans = 0;
        for i in 0..n {
            let need = n-i-1;
            let mut j = i;
            while j < n && zeros[j] < need { j += 1; }
            if j == n { return -1; }
            while j > i {
                zeros.swap(j, j-1);
                ans += 1;
                j -= 1;
            }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
    minSwaps(grid: number[][]): number {
        const n = grid.length;
        const zeros = Array(n).fill(0);
        for (let i = 0; i < n; i++) {
            let cnt = 0;
            for (let j = n-1; j >= 0; j--) {
                if (grid[i][j] === 0) cnt++;
                else break;
            }
            zeros[i] = cnt;
        }
        let ans = 0;
        for (let i = 0; i < n; i++) {
            const need = n-i-1;
            let j = i;
            while (j < n && zeros[j] < need) j++;
            if (j === n) return -1;
            while (j > i) {
                [zeros[j], zeros[j-1]] = [zeros[j-1], zeros[j]];
                ans++;
                j--;
            }
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n^2) — For each row, may scan all rows below.
  • 🧺 Space complexity: O(n) — For zeros array.