Minimum Time to Collect All Apples in a Tree

Problem

Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at vertex 0 and coming back to this vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [ai, bi] means that exists an edge connecting the vertices ai and bi. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple; otherwise, it does not have any apple.

Examples

Example 1:

graph TD
    0(0)
    1(1)
    2("2 🍎")
    3(3)
    4("4 🍎")
    5("5 🍎")
    6(6)
    0 --- 1 & 2
    1 --- 4 & 5
    2 --- 3 & 6

    0 --> 1
    1 --> 0
    
    1 --> 4
    4 --> 1
    
    1 --> 5
    5 --> 1
    
    0 --> 2
    2 --> 0

    %% Style the green, bold directional edges (optimal path)
    linkStyle 6 stroke:green,stroke-width:4px;
    linkStyle 7 stroke:green,stroke-width:4px;
    linkStyle 8 stroke:green,stroke-width:4px;
    linkStyle 9 stroke:green,stroke-width:4px;
    linkStyle 10 stroke:green,stroke-width:4px;
    linkStyle 11 stroke:green,stroke-width:4px;
    linkStyle 12 stroke:green,stroke-width:4px;
    linkStyle 13 stroke:green,stroke-width:4px;

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8 
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

Example 2:

graph TD
    0(0)
    1(1)
    2("2 🍎")
    3(3)
    4(4)
    5("5 🍎")
    6(6)
    0 --- 1 & 2
    1 --- 4 & 5
    2 --- 3 & 6

    0 --> 1
    1 --> 0
    1 --> 5
    5 --> 1
    0 --> 2
    2 --> 0

    %% Style the green, bold directional edges (optimal path)
    linkStyle 6 stroke:green,stroke-width:4px;
    linkStyle 7 stroke:green,stroke-width:4px;
    linkStyle 8 stroke:green,stroke-width:4px;
    linkStyle 9 stroke:green,stroke-width:4px;
    linkStyle 10 stroke:green,stroke-width:4px;
    linkStyle 11 stroke:green,stroke-width:4px;

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

Example 3:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
Output: 0

Solution

Method 1 - DFS

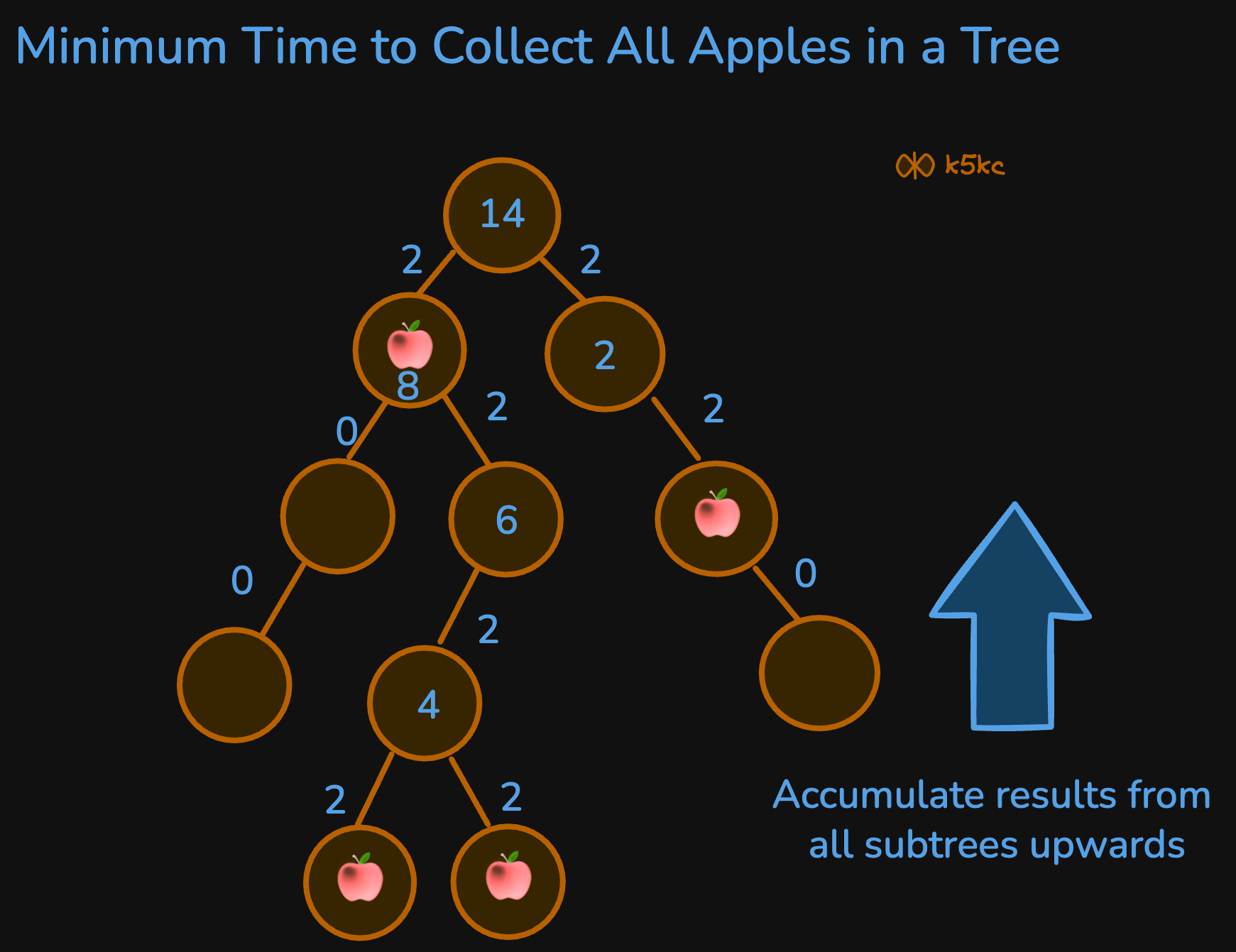
Intuition

The main idea is to use DFS to traverse the tree from the root, only counting the cost to visit subtrees that contain at least one apple. If a subtree (including the current node) has no apples, we skip it. Otherwise, we add 2 seconds for each edge traversed (to go and return), except for the root node, which does not require a return trip.

Approach

1. Build the tree as an adjacency list from the edge list.
2. Use a DFS function that:
   • Marks nodes as visited to avoid cycles.
   • Recursively computes the cost for all children.
   • If a child or the current node has an apple, add the cost for traversing to that child (2 seconds).
   • If neither the current node nor any of its descendants have apples, return 0 for this branch.
3. Start DFS from the root (node 0) with an initial cost of 0.
4. Return the total cost computed by DFS.

Code

C++

class Solution {
public:
    unordered_map<int, vector<int>> g; // to store the graph
    unordered_map<int, bool> visited; // to stop exploring same nodes again and again.
    
    void createGraph(vector<vector<int>>& edges) {
      for (auto e: edges) {
        g[e[0]].push_back(e[1]);
        g[e[1]].push_back(e[0]);
      }
    }
  
    int dfs(int node, int myCost, vector<bool>& hasApple) {
      if (visited[node]) {
          return 0;
      }
      visited[node] = true;
      
      int childrenCost = 0; // cost of traversing all children. 
      for (auto x: g[node]) { 
        childrenCost += dfs(x, 2, hasApple);  // check recursively for all apples.
      }

      if (childrenCost == 0 && hasApple[node] == false) {
        return 0;
      }
      return (childrenCost + myCost);
    }
  
    int minTime(int n, vector<vector<int>>& edges, vector<bool>& hasApple) {
      createGraph(edges); // construct the graph first.
      return dfs(0, 0, hasApple); // cost of reaching the root is 0. For all others, its 2.
    }
};

Java

class Solution {
    public int minTime(int n, int[][] edges, List<Boolean> hasApple) {
        
        Map<Integer, List<Integer>> graph = createGraph(edges); // to store the graph
        Map<Integer, Boolean> visited = new HashMap<>();
		
        return dfs(graph, 0, hasApple, 0, visited); // cost of reaching the root is 0. For all others, its 2.
      
    }
    
    private int dfs(Map<Integer, List<Integer>> graph, int node, List<Boolean> hasApple, int myCost, Map<Integer, Boolean> visited) {
        Boolean v = visited.getOrDefault(node, false);
		if (v) {
			return 0;
		}
		visited.put(node, true);
		
        int childrenCost = 0; // cost of traversing all children. 
      
        for(int n : graph.getOrDefault(node, new ArrayList<>())) {
            childrenCost += dfs(graph, n, hasApple, 2, visited); // check recursively for all apples in subtrees.
        }
      
        if (childrenCost == 0 && hasApple.get(node) == false) {
          // If no child has apples, then we won't traverse the subtree, so cost will be zero.
          // similarly, if current node also does not have the apple, we won't traverse this branch at all, so cost will be zero.
          return 0;
        }
      
        return childrenCost + myCost;
    }
    
    private Map<Integer, List<Integer>> createGraph(int[][] edges) {
        Map<Integer, List<Integer>> graph = new HashMap<>();
      
        for(int i = 0; i < edges.length; i++) {
            List<Integer> list = graph.getOrDefault(edges[i][0], new ArrayList<>()); // Adjecency list representation.
            list.add(edges[i][1]);
            graph.put(edges[i][0], list);
			
			list = graph.getOrDefault(edges[i][1], new ArrayList<>()); // Adjecency list representation.
            list.add(edges[i][0]);
            graph.put(edges[i][1], list);
        }
      
        return graph;
    }
}

Python

class Solution:
	def minTime(self, n: int, edges: List[List[int]], hasApple: List[bool]) -> int:
	    adj = [[] for _ in range(n)]
	    for u, v in edges:
	        adj[u].append(v)
	        adj[v].append(u)
	
	    visited = set()
	    def dfs(node):
	        if node in visited:
	            return 0
	        visited.add(node)
	        secs = 0
	        for child in adj[node]:
	            secs += dfs(child)
	        if secs > 0:
	            return secs + 2
	        return 2 if hasApple[node] else 0
	
	    return max(dfs(0) - 2, 0)

Rust

use std::collections::HashMap;

impl Solution {
    pub fn min_time(n: i32, edges: Vec<Vec<i32>>, has_apple: Vec<bool>) -> i32 {
        let mut graph: HashMap<i32, Vec<i32>> = HashMap::new();
        let mut start = 0;
        for i in 0..n {
            graph.insert(i, vec![]);
        }
        for edge in edges.iter() {
            graph.get_mut(&edge[0]).unwrap().push(edge[1]);
            graph.get_mut(&edge[1]).unwrap().push(edge[0]);
        }
        Self::dfs(&graph, &has_apple, 0, -1)
    }

    fn dfs(graph: &HashMap<i32, Vec<i32>>, has_apple: &Vec<bool>, node: i32, prev: i32) -> i32 {
        let mut ans = 0;
        for &nei in graph.get(&node).unwrap() {
            if nei == prev {
                continue;
            }
            let sub_ans = Self::dfs(graph, has_apple, nei, node);
            if sub_ans > 0 || has_apple[nei as usize] {
                ans += sub_ans + 2;
            }
        }
        ans
    }



}

Complexity

• ⏰ Time complexity: O(n), where n is the number of nodes, since each node and edge is visited at most once during DFS.
• 🧺 Space complexity: O(n), for the adjacency list, visited map, and recursion stack.