problemeasyalgorithmsleetcode-1266leetcode 1266leetcode1266

Minimum Time Visiting All Points

EasyUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

On a 2D plane, there are n points with integer coordinates points[i] = [xi, yi]. Return _theminimum time in seconds to visit all the points in the order given by _points.

You can move according to these rules:

  • In 1 second, you can either:
  • move vertically by one unit,
  • move horizontally by one unit, or
  • move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in 1 second).
    • You have to visit the points in the same order as they appear in the array.
    • You are allowed to pass through points that appear later in the order, but these do not count as visits.

Examples

Example 1


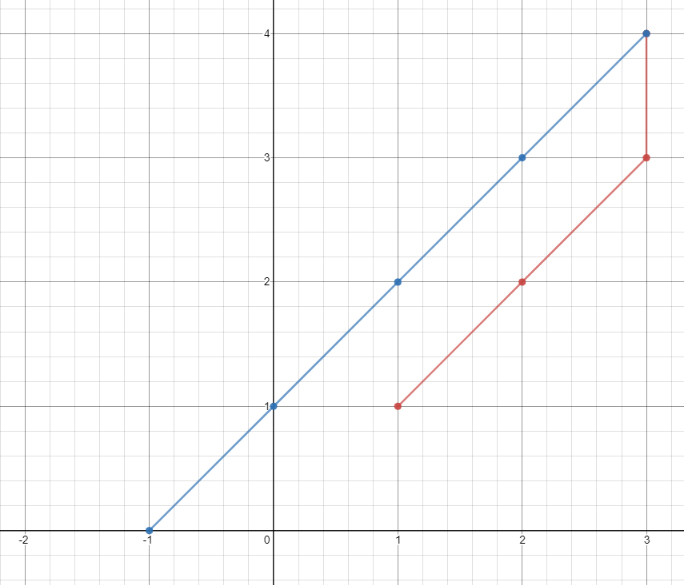
![](https://assets.leetcode.com/uploads/2019/11/14/1626_example_1.PNG)

Input: points = [[1,1],[3,4],[-1,0]]
Output: 7
Explanation: One optimal path is **[1,1]** -> [2,2] -> [3,3] -> **[3,4]** -> [2,3] -> [1,2] -> [0,1] -> **[-1,0]**   
Time from [1,1] to [3,4] = 3 seconds 
Time from [3,4] to [-1,0] = 4 seconds
Total time = 7 seconds

Example 2

Input: points = [[3,2],[-2,2]]
Output: 5

Constraints

  • points.length == n
  • 1 <= n <= 100
  • points[i].length == 2
  • -1000 <= points[i][0], points[i][1] <= 1000

Solution

Method 1 – Greedy Manhattan/Diagonal Moves

Intuition

To minimize time, always move diagonally as much as possible, since a diagonal move covers both axes in one second. The minimum time between two points is the maximum of the differences in x and y coordinates.

Approach

  1. Iterate through each consecutive pair of points.
  2. For each pair, compute dx = abs(x2 - x1) and dy = abs(y2 - y1).
  3. Add max(dx, dy) to the total time.
  4. Return the total time.

Code

C++
class Solution {
public:
    int minTimeToVisitAllPoints(vector<vector<int>>& points) {
        int ans = 0;
        for (int i = 1; i < points.size(); ++i) {
            int dx = abs(points[i][0] - points[i-1][0]);
            int dy = abs(points[i][1] - points[i-1][1]);
            ans += max(dx, dy);
        }
        return ans;
    }
};
Go
func MinTimeToVisitAllPoints(points [][]int) int {
    ans := 0
    for i := 1; i < len(points); i++ {
        dx := abs(points[i][0] - points[i-1][0])
        dy := abs(points[i][1] - points[i-1][1])
        if dx > dy {
            ans += dx
        } else {
            ans += dy
        }
    }
    return ans
}
func abs(x int) int { if x < 0 { return -x } else { return x } }
Java
class Solution {
    public int minTimeToVisitAllPoints(int[][] points) {
        int ans = 0;
        for (int i = 1; i < points.length; i++) {
            int dx = Math.abs(points[i][0] - points[i-1][0]);
            int dy = Math.abs(points[i][1] - points[i-1][1]);
            ans += Math.max(dx, dy);
        }
        return ans;
    }
}
Kotlin
class Solution {
    fun minTimeToVisitAllPoints(points: Array<IntArray>): Int {
        var ans = 0
        for (i in 1 until points.size) {
            val dx = kotlin.math.abs(points[i][0] - points[i-1][0])
            val dy = kotlin.math.abs(points[i][1] - points[i-1][1])
            ans += maxOf(dx, dy)
        }
        return ans
    }
}
Python
from typing import List
class Solution:
    def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:
        ans = 0
        for i in range(1, len(points)):
            dx = abs(points[i][0] - points[i-1][0])
            dy = abs(points[i][1] - points[i-1][1])
            ans += max(dx, dy)
        return ans
Rust
impl Solution {
    pub fn min_time_to_visit_all_points(points: Vec<Vec<i32>>) -> i32 {
        let mut ans = 0;
        for i in 1..points.len() {
            let dx = (points[i][0] - points[i-1][0]).abs();
            let dy = (points[i][1] - points[i-1][1]).abs();
            ans += dx.max(dy);
        }
        ans
    }
}
TypeScript
class Solution {
    minTimeToVisitAllPoints(points: number[][]): number {
        let ans = 0;
        for (let i = 1; i < points.length; i++) {
            const dx = Math.abs(points[i][0] - points[i-1][0]);
            const dy = Math.abs(points[i][1] - points[i-1][1]);
            ans += Math.max(dx, dy);
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n) — We scan the points once.
  • 🧺 Space complexity: O(1) — Only a few variables are used for computation.

Comments