Problem

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens’ placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.

Definition of Attack

In chess, a queen can move as far as she pleases, horizontally, vertically, or diagonally. A chess board has 8 rows and 8 columns. The standard 8 by 8 Queen’s problem asks how to place 8 queens on an ordinary chess board so that none of them can hit any other in one move.(Source: http://www.math.utah.edu/~alfeld/queens/queens.html)

Here is one case for 8x8 board where queens dont attack each other.

Here is 1 possible solution for n-queen, for n = 8.

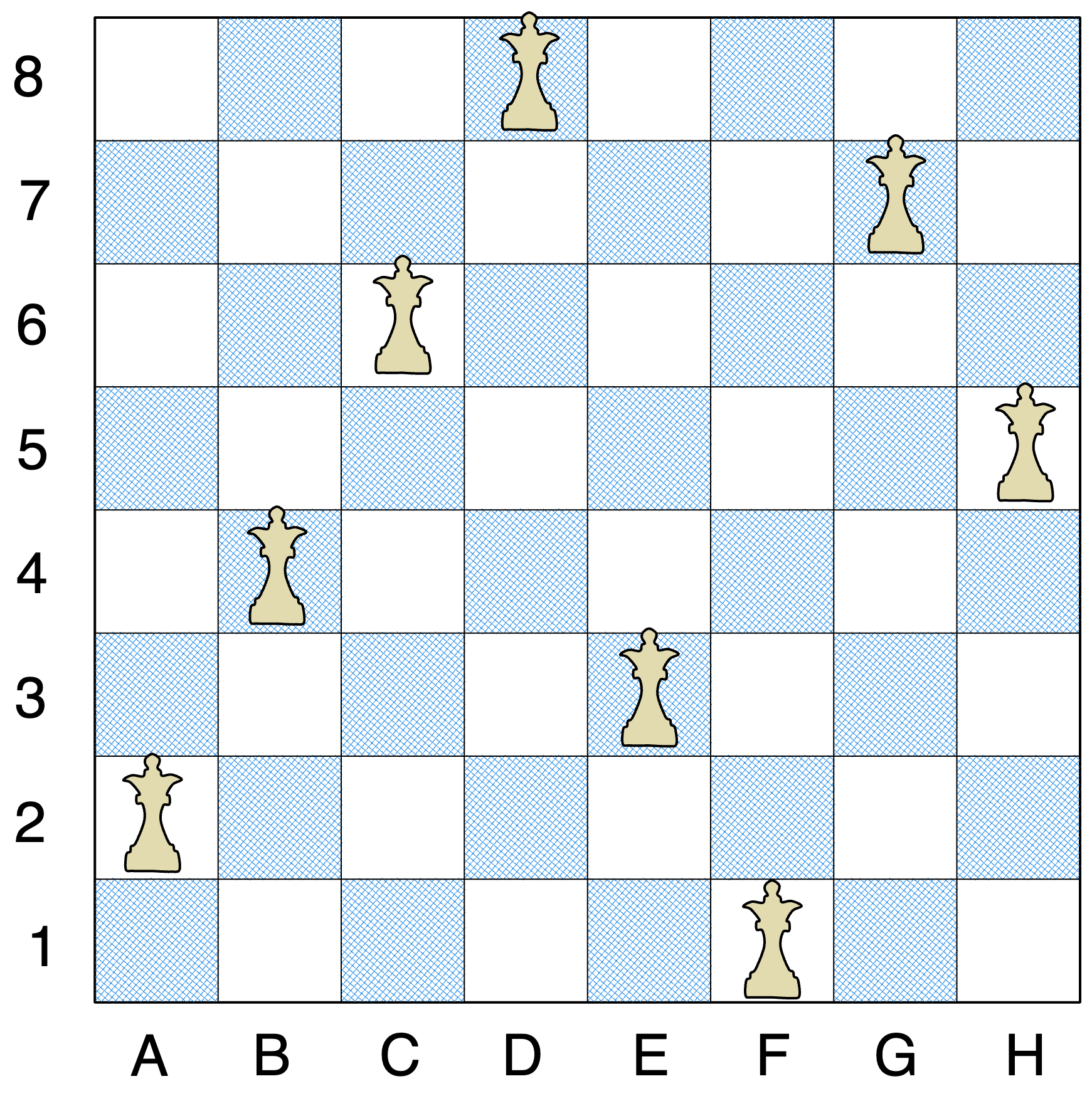
Examples

Example 1:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

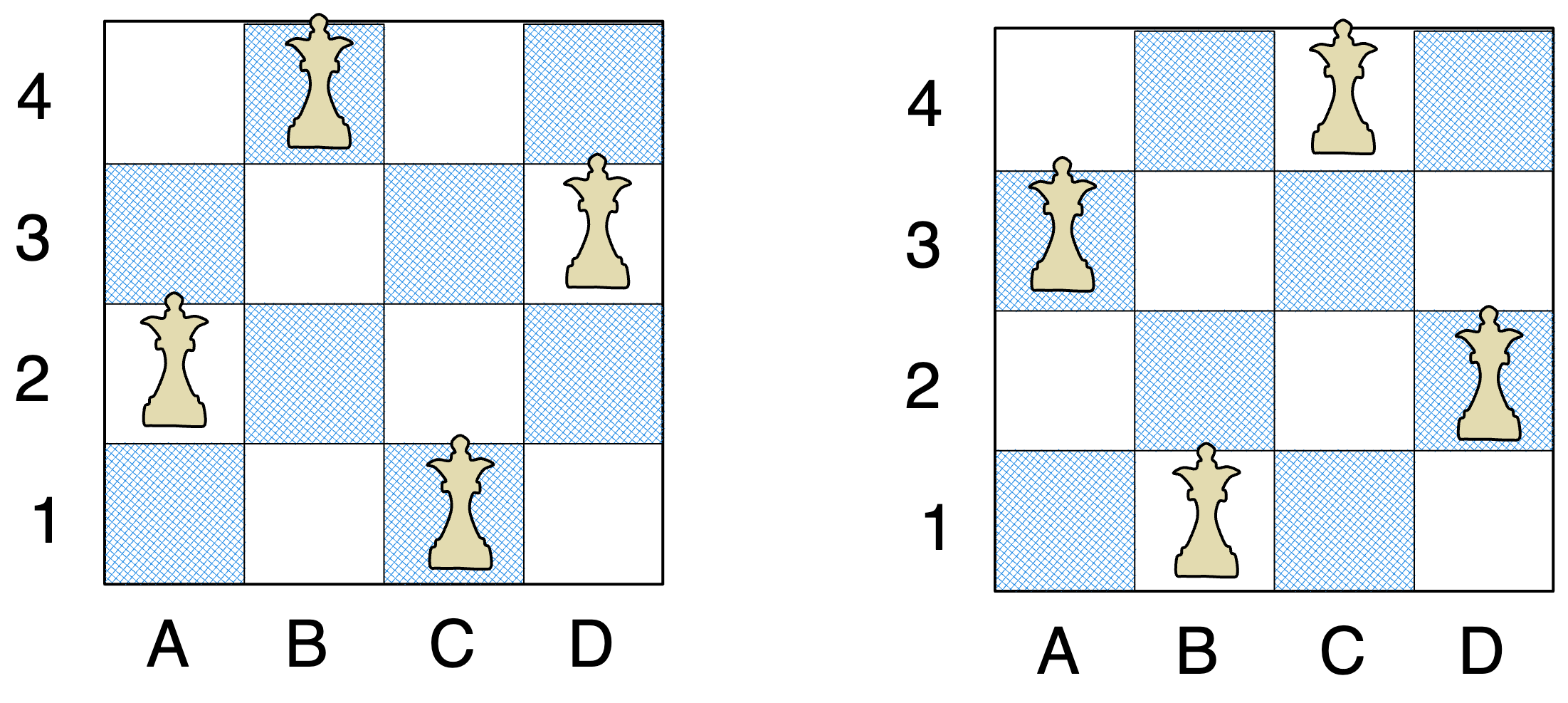
Input: n = 4
Output:
[
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]

Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above

Solution

Method 1 - Backtracking Using O(N^2) Space Matrix

The N Queen Problem is one of the best problem used to teach backtracking and of course recursion. Backtracking is a general algorithm which finds all complete solutions to a problem by building over partial solutions. In this process, the problem might reach to a partial solution which may not result into a complete solution. Such partial solutions are effectively rejected by the backtracking algorithm.

What Are Major & Minor Diagonals ?

With respect to a cell(i, j), the major diagonal contains all the cells [(i+2, j+2), (i+1, j+1), (i, j), (i-1, j-1), (i-2, j-2), (i-3, j-3)] till the limits of the board. On similar lines the minor diagonal contains all the cells [(i+2, j-2), (i+1, j-1), (i, j), (i-1, j+1), (i-2, j+2), (i-3, j+3)] and so on till the limits of the board. Here is a pictorial representation for the same. The blue ones are major diagonals and the red ones are minor diagonals.

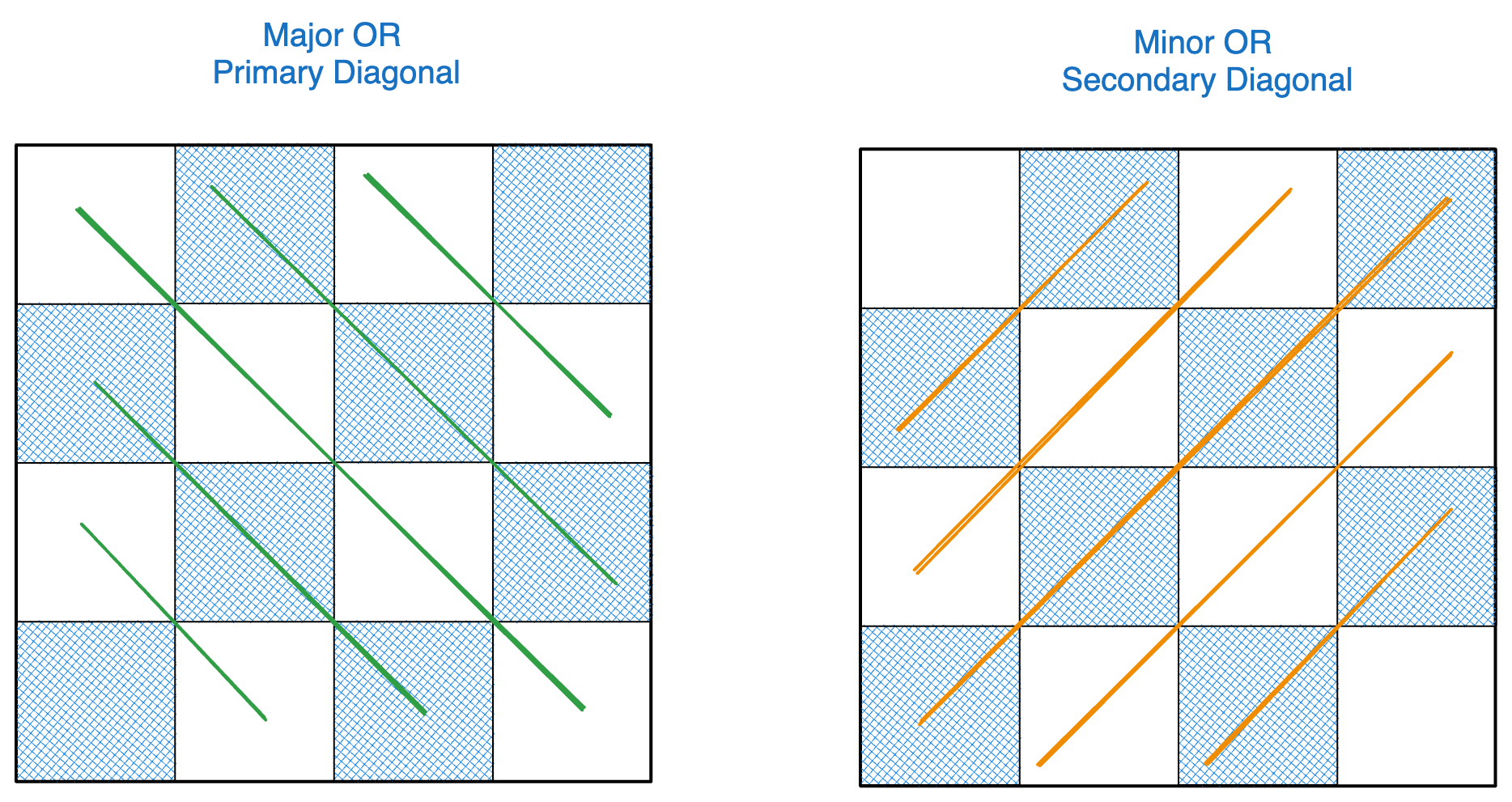
It is evident that we need a method which can check if the current cell is safe.

Algo:

  1. Place the queens column wise, start from the left most column
  2. If all queens are placed - return true and add the solution matrix.
  3. Let x be row and y be col, where we are placing queen Q. Every time we find a existing ‘Q’, 3 conditions need to be met before we can place a new ‘Q’ in the new column:
    1. no confict in columns : self explanatory as we put ‘Q’ col by col.
    2. no confict in rows : x == i
    3. no conflict in diagonals : Math.abs(x-i) == Math.abs(y-j)
  4. If all the rows are tried and nothing worked, return false and print NO SOLUTION.

Here is the approach:

  • Create a solution matrix of the same structure as chess board.
  • Whenever place a queen in the chess board, mark that particular cell in solution matrix.
  • At the end print the solution matrix, the marked cells will show the positions of the queens in the chess board.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

public List<List<String>> solveNQueens(int n) {
	char[][] board = new char[n][n];
	for (int i = 0; i<n; i++) {
		for (int j = 0; j<n; j++) {
			board[i][j] = '.';
		}
	}
	List<List<String>> ans = new ArrayList<List<String>> ();
	dfs(board, 0, ans);
	return ans;
}

private void dfs(char[][] board, int colIndex, List<List<String>> ans) {
	if (colIndex == board.length) {
		ans.add(constructSolution(board));
		return;
	}

	for (int i = 0; i<board.length; i++) {
		if (isSafe(board, i, colIndex)) {
			board[i][colIndex] = 'Q';
			dfs(board, colIndex + 1, ans);
			board[i][colIndex] = '.';
		}
	}
}

private boolean isSafe(char[][] board, int x, int y) {
	for (int i = 0; i<board.length; i++) {
		for (int j = 0; j<y; j++) {
			if (board[i][j] == 'Q' && (x + j == y + i || x + y == i + j || x == i)) {
				return false;
			}
		}
	}

	return true;
}

private List<String> constructSolution(char[][] board) {
	List<String> subAns = new LinkedList<String> ();
	for (int i = 0; i<board.length; i++) {
		String s = new String(board[i]);
		subAns.add(s);
	}
	return subAns;
}
1
2


We can also write a bit verbose `isSafe()` function:
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

private boolean isValid(char[][] board, int x, int y) {
	// check rows from top to bottom
	for (int i = 0; i<board.length; i++) {
		if (board[i][y] == 'Q') {
			return false;
		}
	}

	// check diag, top left to right bottom
	for (int i = x - 1, j = y - 1; i >= 0 && j >= 0; i--, j--) {
		if (board[i][j] == 'Q') {
			return false;
		}
	}

	// check diag, top right to left bottom
	for (int i = x - 1, j = y + 1; i >= 0 && j<board[0].length; i--, j++) {
		if (board[i][j] == 'Q') {
			return false;
		}
	}

	return true;
}

Method 2 - Backtracking Using O(N) Space Row

Solution matrix takes O(N^2) space. We can reduce it to O(N). We will solve it by taking one dimensional array and consider solution[1] = 2 as “Queen at 1st row is placed at 2nd column.

1

result[i]=j means queen at i-th row is placed at j-th column

Check if Queens placed at (x1, y1) and (x2, y2) are safe

  • x1==x2 means same rows,
  • y1==y2 means same columns
  • |x2-x1|==|y2-y1| means they are placed in diagonals.
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

public List<List<String>> solveNQueens(int n) {
	List<List<String>> ans = new ArrayList<>();
	dfs(0, new int[n], ans);
	return ans;
}

public void dfs(int rowIdx, int[] row, List<List<String>> ans) {
	int n = row.length;
	if (rowIdx == n) {
		ans.add(constructSolution(row));
		return;
	}
	for (int c = 0; c < n; c++) {
		boolean ok = true;
		row[rowIdx] = c;
		for (int r = 0; r < rowIdx; r++) {
			if (row[rowIdx] == row[r] || rowIdx - row[rowIdx] == r - row[r] || rowIdx + row[rowIdx] == r + row[r]) {
				ok = false;
				break;
			}
		}
		if (ok) {
			dfs(rowIdx + 1, row, ans);
		}
	}

}

public List<String> constructSolution(int[] row) {
	int n = row.length;
	List<String> subAns = new ArrayList<>(row.length);
	for (int i = 0; i < n; i++) {
		StringBuilder line = new StringBuilder();
		for (int j = 0; j < n; j++)
			if (j == row[i]) {
				line.append("Q");
			} else {
				line.append(".");
			}
		subAns.add(line.toString());
	}
	return subAns;
}

Analysis for N Queen Problem

  • Time Complexity: O(N! * N)
  • Space Complexity: O(N^2) OR O(N) depending on solution picked.

Space complexity

For this algorithm it is O(N). The algorithm uses an auxiliary array of length N to store just N positions.

Time complexity

  • The isSafe method takes O(N) time as it iterates through our array every time.
  • For each invocation of the placeQueen method, there is a loop which runs for O(N) time.
  • In each iteration of this loop, there is isSafe invocation which is O(N) and a recursive call with a smaller argument.

If we add all this up and define the run time as T(N). Then T(N) = O(N2) + N*T(N-1). If you draw a recursion tree using this recurrence, the final term will be something like n3+ n! O(1). By the definition of Big O, this can be reduced to O(n!) running time. Let me know in comments if you are not able to derive the n! from the recurrence, I will try to draw the recursion tree.