Problem

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return the number of distinct solutions to the n-queens puzzle.

Examples

Example 1:

1
2
3

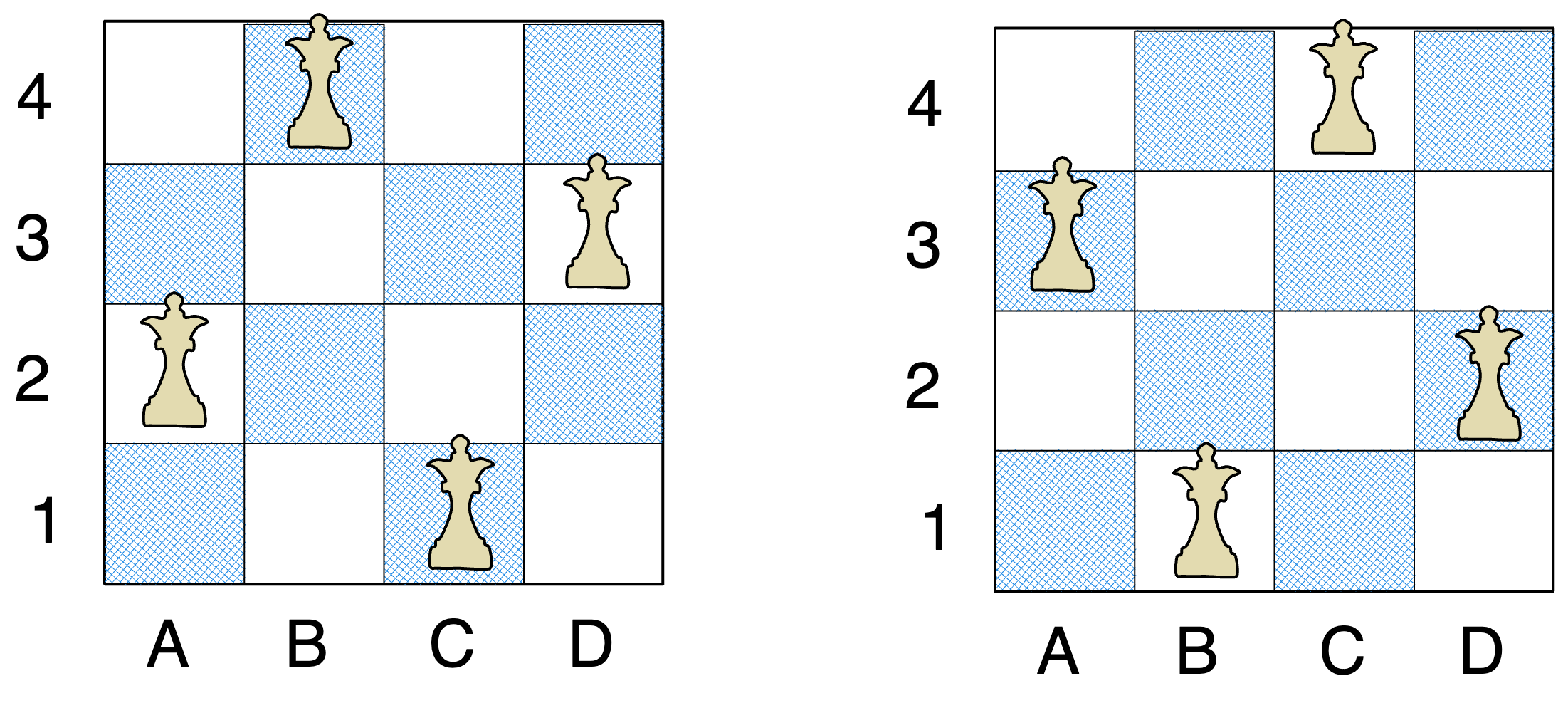
Input: n = 4
Output: 2
Explanation: There are two distinct solutions to the 4-queens puzzle as shown.

Example 2:

1
2

Input: n = 1
Output: 1

Solution

We have already seen N-Queens. We can use backtracking similar to that, and may be this problem is bit easier.

Method 1 - Backtracking Using O(N^2) Space Matrix

This is similar to the problem we had solved with O(n^2) matrix in N-Queens. But in dfs, we will not pass a list and also return a count instead of adding solution to list.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

public int totalNQueens(int n) {
	char[][] board = new char[n][n];
	for (char[] row: board) {
		Arrays.fill(row, '.');
	}
	return dfs(board, 0);
}

private int dfs(char[][] board, int colIndex) {
	if (colIndex == board.length) {
		return 1;
	}
	int count = 0;
	for (int i = 0; i<board.length; i++) {
		if (isSafe(board, i, colIndex)) {
			board[i][colIndex] = 'Q';
			count += dfs(board, colIndex + 1);
			board[i][colIndex] = '.';
		}
	}
	return count;
}

private boolean isSafe(char[][] board, int x, int y) {
	for (int i = 0; i<board.length; i++) {
		for (int j = 0; j<y; j++) {
			if (board[i][j] == 'Q' && (x + j == y + i || x + y == i + j || x == i)) {
				return false;
			}
		}
	}

	return true;
}

Method 2 - Backtracking Using O(N) Space Row

Again this is similar to Backtracking Using O(N) Space Row in N-Queens.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

public int totalNQueens(int n) {
	return dfs(0, new int[n]);
}

public int dfs(int cur, int[] row) {
	if (cur == row.length) {
		return 1;
	}
	int count = 0;
	for (int i = 0; i < row.length; i++) {
		boolean ok = true;
		row[cur] = i;
		for (int j = 0; j < cur; j++) {
			if (row[cur] == row[j] || row[cur] - row[j] == cur - j || row[cur] - row[j] == j - cur) {
				ok = false;
				break;
			}
		}
		if (ok) {
			count += dfs(cur + 1, row);
		}
	}
	return count;
}

Complexity

  • ⏰ Time complexity: O(N! * N)
  • 🧺 Space complexity: O(N^2)

Method 3 - Backtracking Using Sets for Row and Diagonals

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

public int totalNQueens(int n) {
    int[] res = new int[1];
    helper(res,n,0);
    return res[0];
}
public void helper(int[] res, int n, int row){
    if(row==n){
        res[0]++;
    }
    else{
        for(int i=0; i<n; i++){
            if(col.contains(i) || diag1.contains(i+row) || diag2.contains(row-i)) continue;
            else{
                col.add(i);
                diag1.add(i+row);
                diag2.add(row-i);
                helper(res,n,row+1);
                col.remove(i);
                diag1.remove(i+row);
                diag2.remove(row-i);
            }
        }
    }
}

Method 4 - Backtracking Using Boolean Arrays for Col and Diagonals

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

public class Solution {
    int count = 0;
    public int totalNQueens(int n) {
        boolean[] cols = new boolean[n];     // columns   |
        boolean[] d1 = new boolean[2 * n];   // diagonals \
        boolean[] d2 = new boolean[2 * n];   // diagonals /
        backtracking(0, cols, d1, d2, n);
        return count;
    }

    public void backtracking(int row, boolean[] cols, boolean[] d1, boolean []d2, int n) {
        if(row == n) count++;

        for(int col = 0; col < n; col++) {
            int id1 = col - row + n;
            int id2 = col + row;
            if(cols[col] || d1[id1] || d2[id2]) continue;

            cols[col] = true; d1[id1] = true; d2[id2] = true;
            backtracking(row + 1, cols, d1, d2, n);
            cols[col] = false; d1[id1] = false; d2[id2] = false;
        }
    }
}