Number Of Corner Rectangles

Problem

Given an m x n integer matrix grid where each entry is only 0 or 1, return the number ofcorner rectangles.

A corner rectangle is four distinct 1's on the grid that forms an axis-aligned rectangle. Note that only the corners need to have the value 1. Also, all four 1's used must be distinct.

Examples

Example 1:

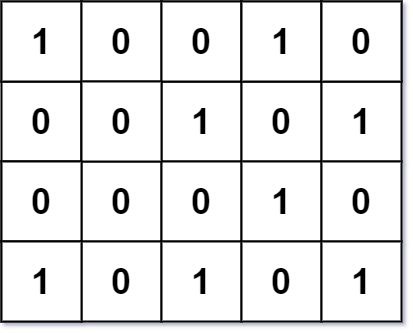
Input: grid = [[1,0,0,1,0],[0,0,1,0,1],[0,0,0,1,0],[1,0,1,0,1]]
Output: 1
Explanation: There is only one corner rectangle, with corners grid[1][2], grid[1][4], grid[3][2], grid[3][4].

Example 2:

Input: grid = [[1,1,1],[1,1,1],[1,1,1]]
Output: 9
Explanation: There are four 2x2 rectangles, four 2x3 and 3x2 rectangles, and one 3x3 rectangle.

Example 3:

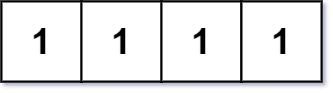
Input: grid = [[1,1,1,1]]
Output: 0
Explanation: Rectangles must have four distinct corners.

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• grid[i][j] is either 0 or 1.
• The number of 1's in the grid is in the range [1, 6000].

Solution

Method 1 – Count Pairs of Columns with 1s

Intuition

For each pair of columns, count how many rows have 1s in both columns. For each such pair, the number of rectangles is C(count, 2) = count*(count-1)/2.

Approach

1. For each row, for each pair of columns with 1s, increment a counter.
2. For each pair, add count*(count-1)/2 to the answer.

Code

C++

#include <vector>
using namespace std;
class Solution {
public:
    int countCornerRectangles(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size(), ans = 0;
        vector<vector<int>> cnt(n, vector<int>(n));
        for (auto& row : grid) {
            for (int i = 0; i < n; ++i) if (row[i])
                for (int j = i+1; j < n; ++j) if (row[j]) {
                    ans += cnt[i][j];
                    cnt[i][j]++;
                }
        }
        return ans;
    }
};

Go

func countCornerRectangles(grid [][]int) int {
    m, n := len(grid), len(grid[0])
    cnt := make([][]int, n)
    for i := range cnt { cnt[i] = make([]int, n) }
    ans := 0
    for _, row := range grid {
        for i := 0; i < n; i++ {
            if row[i] == 1 {
                for j := i+1; j < n; j++ {
                    if row[j] == 1 {
                        ans += cnt[i][j]
                        cnt[i][j]++
                    }
                }
            }
        }
    }
    return ans
}

Java

class Solution {
    public int countCornerRectangles(int[][] grid) {
        int m = grid.length, n = grid[0].length, ans = 0;
        int[][] cnt = new int[n][n];
        for (int[] row : grid) {
            for (int i = 0; i < n; ++i) if (row[i]==1)
                for (int j = i+1; j < n; ++j) if (row[j]==1) {
                    ans += cnt[i][j];
                    cnt[i][j]++;
                }
        }
        return ans;
    }
}

Kotlin

class Solution {
    fun countCornerRectangles(grid: Array<IntArray>): Int {
        val m = grid.size; val n = grid[0].size
        val cnt = Array(n) { IntArray(n) }
        var ans = 0
        for (row in grid) {
            for (i in 0 until n) if (row[i]==1)
                for (j in i+1 until n) if (row[j]==1) {
                    ans += cnt[i][j]
                    cnt[i][j]++
                }
        }
        return ans
    }
}

Python

class Solution:
    def countCornerRectangles(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        cnt = [[0]*n for _ in range(n)]
        ans = 0
        for row in grid:
            for i in range(n):
                if row[i]:
                    for j in range(i+1, n):
                        if row[j]:
                            ans += cnt[i][j]
                            cnt[i][j] += 1
        return ans

Rust

impl Solution {
    pub fn count_corner_rectangles(grid: Vec<Vec<i32>>) -> i32 {
        let m = grid.len(); let n = grid[0].len();
        let mut cnt = vec![vec![0;n];n];
        let mut ans = 0;
        for row in &grid {
            for i in 0..n {
                if row[i]==1 {
                    for j in i+1..n {
                        if row[j]==1 {
                            ans += cnt[i][j];
                            cnt[i][j] += 1;
                        }
                    }
                }
            }
        }
        ans
    }
}

TypeScript

function countCornerRectangles(grid: number[][]): number {
    const m = grid.length, n = grid[0].length;
    const cnt = Array.from({length: n}, () => Array(n).fill(0));
    let ans = 0;
    for (const row of grid) {
        for (let i = 0; i < n; ++i) if (row[i])
            for (let j = i+1; j < n; ++j) if (row[j]) {
                ans += cnt[i][j];
                cnt[i][j]++;
            }
    }
    return ans;
}

Complexity

• ⏰ Time complexity: O(m * n^2)
• 🧺 Space complexity: O(n^2)