problemhardalgorithmsleetcode-1819leetcode 1819leetcode1819

Number of Different Subsequences GCDs

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given an array nums that consists of positive integers.

The GCD of a sequence of numbers is defined as the greatest integer that divides all the numbers in the sequence evenly.

  • For example, the GCD of the sequence [4,6,16] is 2.

A subsequence of an array is a sequence that can be formed by removing some elements (possibly none) of the array.

  • For example, [2,5,10] is a subsequence of [1,2,1,**_2_** ,4,1,_**5**_ ,_**10**_].

Return thenumber of different GCDs among all non-empty subsequences of nums.

Examples

Example 1


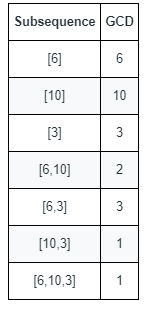
![](https://assets.leetcode.com/uploads/2021/03/17/image-1.png)

Input: nums = [6,10,3]
Output: 5
Explanation: The figure shows all the non-empty subsequences and their GCDs.
The different GCDs are 6, 10, 3, 2, and 1.

Example 2

Input: nums = [5,15,40,5,6]
Output: 7

Constraints

  • 1 <= nums.length <= 10^5
  • 1 <= nums[i] <= 2 * 10^5

Solution

Method 1 – Math, Multiples, and GCD

Intuition

For each possible GCD g, check if there exists a subsequence whose GCD is g. For g to be a GCD, there must be numbers in nums that are multiples of g, and their GCD can be reduced to g by picking appropriate elements. Use a sieve-like approach to check for each g from 1 to max(nums).

Approach

  1. Build a set or boolean array to mark which numbers are present in nums.
  2. For each g from 1 to max(nums), check all multiples of g in nums, and compute their GCD. If the GCD equals g, count it.
  3. Return the total count.

Code

C++
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
    int countDifferentSubsequenceGCDs(vector<int>& nums) {
        int mx = *max_element(nums.begin(), nums.end());
        vector<bool> present(mx+1, false);
        for (int x : nums) present[x] = true;
        int ans = 0;
        for (int g = 1; g <= mx; ++g) {
            int cur = 0;
            for (int m = g; m <= mx; m += g) {
                if (present[m]) cur = gcd(cur, m);
            }
            if (cur == g) ++ans;
        }
        return ans;
    }
    int gcd(int a, int b) { return b ? gcd(b, a % b) : a; }
};
Go
func countDifferentSubsequenceGCDs(nums []int) int {
    mx := 0
    for _, x := range nums { if x > mx { mx = x } }
    present := make([]bool, mx+1)
    for _, x := range nums { present[x] = true }
    ans := 0
    gcd := func(a, b int) int { for b != 0 { a, b = b, a%b }; return a }
    for g := 1; g <= mx; g++ {
        cur := 0
        for m := g; m <= mx; m += g {
            if present[m] { cur = gcd(cur, m) }
        }
        if cur == g { ans++ }
    }
    return ans
}
Java
import java.util.*;
class Solution {
    public int countDifferentSubsequenceGCDs(int[] nums) {
        int mx = Arrays.stream(nums).max().getAsInt();
        boolean[] present = new boolean[mx+1];
        for (int x : nums) present[x] = true;
        int ans = 0;
        for (int g = 1; g <= mx; ++g) {
            int cur = 0;
            for (int m = g; m <= mx; m += g) {
                if (present[m]) cur = gcd(cur, m);
            }
            if (cur == g) ++ans;
        }
        return ans;
    }
    int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }
}
Kotlin
class Solution {
    fun countDifferentSubsequenceGCDs(nums: IntArray): Int {
        val mx = nums.maxOrNull()!!
        val present = BooleanArray(mx+1)
        for (x in nums) present[x] = true
        var ans = 0
        fun gcd(a: Int, b: Int): Int = if (b == 0) a else gcd(b, a % b)
        for (g in 1..mx) {
            var cur = 0
            var m = g
            while (m <= mx) {
                if (present[m]) cur = gcd(cur, m)
                m += g
            }
            if (cur == g) ans++
        }
        return ans
    }
}
Python
from math import gcd
class Solution:
    def countDifferentSubsequenceGCDs(self, nums: List[int]) -> int:
        mx = max(nums)
        present = set(nums)
        ans = 0
        for g in range(1, mx+1):
            cur = 0
            for m in range(g, mx+1, g):
                if m in present:
                    cur = gcd(cur, m)
            if cur == g:
                ans += 1
        return ans
Rust
use std::collections::HashSet;
impl Solution {
    pub fn count_different_subsequence_gcds(nums: Vec<i32>) -> i32 {
        let mx = *nums.iter().max().unwrap();
        let present: HashSet<i32> = nums.into_iter().collect();
        let mut ans = 0;
        for g in 1..=mx {
            let mut cur = 0;
            let mut m = g;
            while m <= mx {
                if present.contains(&m) { cur = gcd(cur, m); }
                m += g;
            }
            if cur == g { ans += 1; }
        }
        ans
    }
}
fn gcd(a: i32, b: i32) -> i32 { if b == 0 { a } else { gcd(b, a % b) } }
TypeScript
function countDifferentSubsequenceGCDs(nums: number[]): number {
    const mx = Math.max(...nums);
    const present = new Set(nums);
    let ans = 0;
    for (let g = 1; g <= mx; ++g) {
        let cur = 0;
        for (let m = g; m <= mx; m += g) {
            if (present.has(m)) cur = gcd(cur, m);
        }
        if (cur === g) ans++;
    }
    return ans;
}
function gcd(a: number, b: number): number { return b === 0 ? a : gcd(b, a % b); }

Complexity

  • ⏰ Time complexity: O(M log M) (M = max(nums))
  • 🧺 Space complexity: O(M)

Comments