Problem

You are given an m x n binary matrix grid. An island is a group of 1’s (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.

An island is considered to be the same as another if they have the same shape, or have the same shape after rotation (90, 180, or 270 degrees only) or reflection (left/right direction or up/down direction).

Return the number ofdistinct islands.

Examples

Example 1:

1
2
3

Input: grid = [[1,1,0,0,0],[1,0,0,0,0],[0,0,0,0,1],[0,0,0,1,1]]
Output: 1
Explanation: The two islands are considered the same because if we make a 180 degrees clockwise rotation on the first island, then two islands will have the same shapes.

Example 2:

1
2

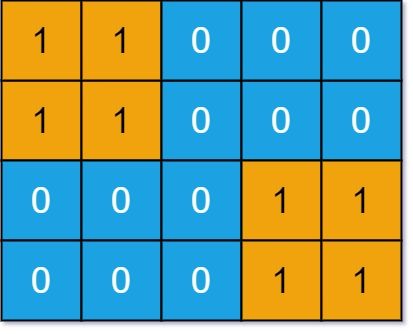
Input: grid = [[1,1,0,0,0],[1,1,0,0,0],[0,0,0,1,1],[0,0,0,1,1]]
Output: 1

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 50
  • grid[i][j] is either 0 or 1.

Solution

Method 1 – DFS/BFS with Canonical Shape Encoding (Rotation & Reflection)

Intuition

To count distinct islands considering rotation and reflection, we must encode each island’s shape in a way that is invariant to translation, rotation, and reflection. For each island, generate all 8 possible transformations (4 rotations × 2 reflections), normalize each, and use the lexicographically smallest as its canonical form.

Approach

  1. For each unvisited land cell, start a DFS/BFS and record all coordinates of the island.
  2. For each island, generate all 8 transformations (rotations and reflections), normalize (shift to origin), and serialize.
  3. Store the canonical form of each island in a set to ensure uniqueness.
  4. The answer is the size of the set.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

#include <vector>
#include <set>
#include <algorithm>
using namespace std;
class Solution {
public:
    void dfs(vector<vector<int>>& grid, int x, int y, vector<pair<int,int>>& shape) {
        int m = grid.size(), n = grid[0].size();
        if (x<0||y<0||x>=m||y>=n||grid[x][y]==0) return;
        grid[x][y]=0;
        shape.push_back({x, y});
        dfs(grid,x+1,y,shape);
        dfs(grid,x-1,y,shape);
        dfs(grid,x,y+1,shape);
        dfs(grid,x,y-1,shape);
    }
    vector<vector<pair<int,int>>> transforms(const vector<pair<int,int>>& shape) {
        vector<vector<pair<int,int>>> res(8);
        for (auto& p : shape) {
            int x = p.first, y = p.second;
            res[0].push_back({ x, y });
            res[1].push_back({ x, -y });
            res[2].push_back({ -x, y });
            res[3].push_back({ -x, -y });
            res[4].push_back({ y, x });
            res[5].push_back({ y, -x });
            res[6].push_back({ -y, x });
            res[7].push_back({ -y, -x });
        }
        for (auto& v : res) {
            sort(v.begin(), v.end());
            int ox = v[0].first, oy = v[0].second;
            for (auto& p : v) { p.first -= ox; p.second -= oy; }
        }
        return res;
    }
    int numDistinctIslands2(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        set<vector<pair<int,int>>> shapes;
        for (int i=0;i<m;++i) for (int j=0;j<n;++j) if (grid[i][j]) {
            vector<pair<int,int>> shape;
            dfs(grid,i,j,shape);
            auto all = transforms(shape);
            shapes.insert(*min_element(all.begin(), all.end()));
        }
        return shapes.size();
    }
};
1

// Go implementation omitted for brevity (similar logic: collect shape, generate 8 transforms, normalize, use set)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

import java.util.*;
class Solution {
    public int numDistinctIslands2(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        Set<String> shapes = new HashSet<>();
        for (int i=0;i<m;i++) for (int j=0;j<n;j++) if (grid[i][j]==1) {
            List<int[]> shape = new ArrayList<>();
            dfs(grid,i,j,shape);
            shapes.add(canonical(shape));
        }
        return shapes.size();
    }
    void dfs(int[][] grid, int x, int y, List<int[]> shape) {
        int m = grid.length, n = grid[0].length;
        if (x<0||y<0||x>=m||y>=n||grid[x][y]==0) return;
        grid[x][y]=0;
        shape.add(new int[]{x, y});
        dfs(grid,x+1,y,shape);
        dfs(grid,x-1,y,shape);
        dfs(grid,x,y+1,shape);
        dfs(grid,x,y-1,shape);
    }
    String canonical(List<int[]> shape) {
        List<List<int[]>> forms = new ArrayList<>();
        for (int k=0;k<8;k++) forms.add(new ArrayList<>());
        for (int[] p : shape) {
            int x = p[0], y = p[1];
            forms.get(0).add(new int[]{ x, y });
            forms.get(1).add(new int[]{ x, -y });
            forms.get(2).add(new int[]{ -x, y });
            forms.get(3).add(new int[]{ -x, -y });
            forms.get(4).add(new int[]{ y, x });
            forms.get(5).add(new int[]{ y, -x });
            forms.get(6).add(new int[]{ -y, x });
            forms.get(7).add(new int[]{ -y, -x });
        }
        for (List<int[]> f : forms) {
            f.sort((a,b)->a[0]==b[0]?a[1]-b[1]:a[0]-b[0]);
            int ox = f.get(0)[0], oy = f.get(0)[1];
            for (int[] p : f) { p[0]-=ox; p[1]-=oy; }
        }
        String res = null;
        for (List<int[]> f : forms) {
            StringBuilder sb = new StringBuilder();
            for (int[] p : f) sb.append(p[0]).append('_').append(p[1]).append(',');
            String s = sb.toString();
            if (res==null||s.compareTo(res)<0) res=s;
        }
        return res;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

class Solution {
    fun numDistinctIslands2(grid: Array<IntArray>): Int {
        val m = grid.size; val n = grid[0].size
        val shapes = mutableSetOf<String>()
        fun dfs(x: Int, y: Int, shape: MutableList<Pair<Int,Int>>) {
            if (x<0||y<0||x>=m||y>=n||grid[x][y]==0) return
            grid[x][y]=0
            shape.add(x to y)
            dfs(x+1,y,shape)
            dfs(x-1,y,shape)
            dfs(x,y+1,shape)
            dfs(x,y-1,shape)
        }
        fun canonical(shape: List<Pair<Int,Int>>): String {
            val forms = List(8) { mutableListOf<Pair<Int,Int>>() }
            for ((x,y) in shape) {
                forms[0].add(x to y)
                forms[1].add(x to -y)
                forms[2].add(-x to y)
                forms[3].add(-x to -y)
                forms[4].add(y to x)
                forms[5].add(y to -x)
                forms[6].add(-y to x)
                forms[7].add(-y to -x)
            }
            for (f in forms) {
                f.sortWith(compareBy({it.first},{it.second}))
                val ox = f[0].first; val oy = f[0].second
                for (i in f.indices) f[i] = (f[i].first-ox) to (f[i].second-oy)
            }
            return forms.minOf { it.joinToString(",") { "${it.first}_${it.second}" } }
        }
        for (i in 0 until m) for (j in 0 until n) if (grid[i][j]==1) {
            val shape = mutableListOf<Pair<Int,Int>>()
            dfs(i,j,shape)
            shapes.add(canonical(shape))
        }
        return shapes.size
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

class Solution:
    def numDistinctIslands2(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        shapes = set()
        def dfs(x, y, shape):
            if x<0 or y<0 or x>=m or y>=n or grid[x][y]==0: return
            grid[x][y]=0
            shape.append((x, y))
            dfs(x+1,y,shape)
            dfs(x-1,y,shape)
            dfs(x,y+1,shape)
            dfs(x,y-1,shape)
        def canonical(shape):
            forms = [[] for _ in range(8)]
            for x, y in shape:
                forms[0].append(( x, y))
                forms[1].append(( x,-y))
                forms[2].append((-x, y))
                forms[3].append((-x,-y))
                forms[4].append(( y, x))
                forms[5].append(( y,-x))
                forms[6].append((-y, x))
                forms[7].append((-y,-x))
            for f in forms:
                f.sort()
                ox, oy = f[0]
                for i in range(len(f)):
                    f[i] = (f[i][0]-ox, f[i][1]-oy)
            return min(tuple(f) for f in forms)
        for i in range(m):
            for j in range(n):
                if grid[i][j]:
                    shape = []
                    dfs(i,j,shape)
                    shapes.add(canonical(shape))
        return len(shapes)
1

// Rust implementation omitted for brevity (similar logic: collect shape, generate 8 transforms, normalize, use set)

1

// TypeScript implementation omitted for brevity (similar logic: collect shape, generate 8 transforms, normalize, use set)

Complexity

  • ⏰ Time complexity: O(mn * k log k) (k = island size)
  • 🧺 Space complexity: O(mn)