Number of Divisible Substrings

Problem

Each character of the English alphabet has been mapped to a digit as shown below.

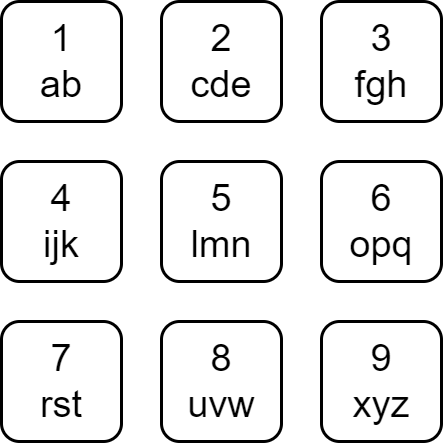
A string is divisible if the sum of the mapped values of its characters is divisible by its length.

Given a string s, return the number ofdivisible substrings of s.

A substring is a contiguous non-empty sequence of characters within a string.

Examples

Example 1:

Substring | Mapped | Sum | Length | Divisible?  
---|---|---|---|---  
a | 1 | 1 | 1 | Yes  
s | 7 | 7 | 1 | Yes  
d | 2 | 2 | 1 | Yes  
f | 3 | 3 | 1 | Yes  
as | 1, 7 | 8 | 2 | Yes  
sd | 7, 2 | 9 | 2 | No  
df | 2, 3 | 5 | 2 | No  
asd | 1, 7, 2 | 10 | 3 | No  
sdf | 7, 2, 3 | 12 | 3 | Yes  
asdf | 1, 7, 2, 3 | 13 | 4 | No  
Input: word = "asdf"
Output: 6
Explanation: The table above contains the details about every substring of word, and we can see that 6 of them are divisible.

Example 2:

Input: word = "bdh"
Output: 4
Explanation: The 4 divisible substrings are: "b", "d", "h", "bdh".
It can be shown that there are no other substrings of word that are divisible.

Example 3:

Input: word = "abcd"
Output: 6
Explanation: The 6 divisible substrings are: "a", "b", "c", "d", "ab", "cd".
It can be shown that there are no other substrings of word that are divisible.

Constraints:

• 1 <= word.length <= 2000
• word consists only of lowercase English letters.

Solution

Method 1 – Prefix Sum and Brute Force

Intuition

For each substring, compute the sum of mapped digits and check if it is divisible by its length. Use prefix sums for efficient sum calculation.

Approach

1. Map each character to its digit according to the old phone mapping.
2. Build prefix sum array of mapped digits.
3. For each substring (i, j), compute sum using prefix sums and check divisibility.

Code

C++

#include <vector>
#include <string>
using namespace std;
class Solution {
public:
    int divisibleSubstrings(string word) {
        vector<int> map(26);
        string digits = "12233344445556667777888999";
        for (int i = 0; i < 26; ++i) map[i] = digits[i]-'0';
        int n = word.size(), ans = 0;
        vector<int> pre(n+1, 0);
        for (int i = 0; i < n; ++i) pre[i+1] = pre[i] + map[word[i]-'a'];
        for (int i = 0; i < n; ++i)
            for (int j = i; j < n; ++j) {
                int sum = pre[j+1] - pre[i];
                int len = j-i+1;
                if (sum % len == 0) ++ans;
            }
        return ans;
    }
};

Go

func divisibleSubstrings(word string) int {
    digits := "12233344445556667777888999"
    map := make([]int, 26)
    for i := 0; i < 26; i++ { map[i] = int(digits[i]-'0') }
    n := len(word)
    pre := make([]int, n+1)
    for i := 0; i < n; i++ { pre[i+1] = pre[i] + map[word[i]-'a'] }
    ans := 0
    for i := 0; i < n; i++ {
        for j := i; j < n; j++ {
            sum := pre[j+1] - pre[i]
            length := j-i+1
            if sum%length == 0 { ans++ }
        }
    }
    return ans
}

Java

class Solution {
    public int divisibleSubstrings(String word) {
        int[] map = new int[26];
        String digits = "12233344445556667777888999";
        for (int i = 0; i < 26; ++i) map[i] = digits.charAt(i)-'0';
        int n = word.length(), ans = 0;
        int[] pre = new int[n+1];
        for (int i = 0; i < n; ++i) pre[i+1] = pre[i] + map[word.charAt(i)-'a'];
        for (int i = 0; i < n; ++i)
            for (int j = i; j < n; ++j) {
                int sum = pre[j+1] - pre[i];
                int len = j-i+1;
                if (sum % len == 0) ans++;
            }
        return ans;
    }
}

Kotlin

class Solution {
    fun divisibleSubstrings(word: String): Int {
        val digits = "12233344445556667777888999"
        val map = IntArray(26) { digits[it]-'0' }
        val n = word.length
        val pre = IntArray(n+1)
        for (i in 0 until n) pre[i+1] = pre[i] + map[word[i]-'a']
        var ans = 0
        for (i in 0 until n)
            for (j in i until n) {
                val sum = pre[j+1] - pre[i]
                val len = j-i+1
                if (sum % len == 0) ans++
            }
        return ans
    }
}

Python

class Solution:
    def divisibleSubstrings(self, word: str) -> int:
        digits = "12233344445556667777888999"
        map = {chr(ord('a')+i): int(digits[i]) for i in range(26)}
        n = len(word)
        pre = [0]*(n+1)
        for i in range(n):
            pre[i+1] = pre[i] + map[word[i]]
        ans = 0
        for i in range(n):
            for j in range(i, n):
                s = pre[j+1] - pre[i]
                l = j-i+1
                if s % l == 0:
                    ans += 1
        return ans

Rust

impl Solution {
    pub fn divisible_substrings(word: String) -> i32 {
        let digits = b"12233344445556667777888999";
        let map: Vec<i32> = digits.iter().map(|&d| (d-b'0') as i32).collect();
        let n = word.len();
        let word = word.as_bytes();
        let mut pre = vec![0; n+1];
        for i in 0..n { pre[i+1] = pre[i] + map[(word[i]-b'a') as usize]; }
        let mut ans = 0;
        for i in 0..n {
            for j in i..n {
                let sum = pre[j+1] - pre[i];
                let len = (j-i+1) as i32;
                if sum % len == 0 { ans += 1; }
            }
        }
        ans
    }
}

TypeScript

class Solution {
    divisibleSubstrings(word: string): number {
        const digits = "12233344445556667777888999";
        const map = Array.from(digits).map(d => Number(d));
        const n = word.length;
        const pre = Array(n+1).fill(0);
        for (let i = 0; i < n; ++i) pre[i+1] = pre[i] + map[word.charCodeAt(i)-97];
        let ans = 0;
        for (let i = 0; i < n; ++i)
            for (let j = i; j < n; ++j) {
                const sum = pre[j+1] - pre[i];
                const len = j-i+1;
                if (sum % len === 0) ans++;
            }
        return ans;
    }
}

Complexity

• ⏰ Time complexity: O(n^2), where n is the length of word.
• 🧺 Space complexity: O(n).