Number of Flowers in Full Bloom

Problem

You are given a 0-indexed 2D integer array flowers, where flowers[i] = [starti, endi] means the ith flower will be in full bloom from starti to endi (inclusive). You are also given a 0-indexed integer array people of size n, where people[i] is the time that the ith person will arrive to see the flowers.

Return an integer array answer of size n, where answer[i] is the number of flowers that are in full bloom when the ith person arrives.

Examples

Example 1:

1
2
3
4
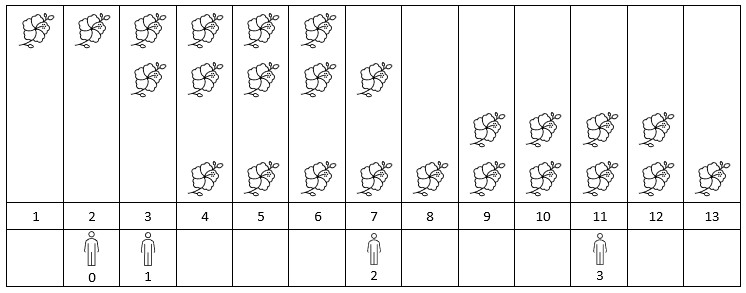
Input: flowers = [[1,6],[3,7],[9,12],[4,13]], people = [2,3,7,11]
Output: [1,2,2,2]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Example 2:

1
2
3
4
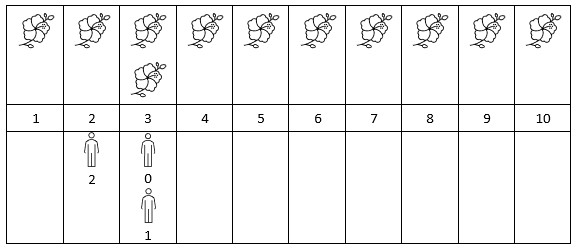
Input: flowers = [[1,10],[3,3]], people = [3,3,2]
Output: [2,2,1]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Solution

Method 1 - Using Binary Search

The problem involves determining for each person, how many flowers are in full bloom at the given time they arrive. We approach this efficiently instead of checking each person’s arrival time against every interval of bloom directly, which can be computationally expensive.

Approach

Separate the start and end times of flowers into two sorted arrays.
For each person’s arrival time (people[i]), use binary search to:
- Count the number of flowers that have started blooming up to the arrival time (using start times).
- Count the flowers that have already finished blooming before the arrival time (using end times).
Subtract the count of flowers that have ended from those that have started blooming to determine the number of flowers in bloom at the given arrival time.
Sorting both start and end arrays enables efficient queries using binary search.
The use of binary search reduces the time complexity compared to brute force iteration.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    public int[] fullBloomFlowers(int[][] flowers, int[] people) {
        int[] starts = Arrays.stream(flowers).mapToInt(f -> f[0]).sorted().toArray();
        int[] ends = Arrays.stream(flowers).mapToInt(f -> f[1]).sorted().toArray();
        
        int[] ans = new int[people.length];
        for (int i = 0; i < people.length; i++) {
            int p = people[i];
            int blooming = upperBound(starts, p) - lowerBound(ends, p);
            ans[i] = blooming;
        }
        
        return ans;
    }
    
    private int upperBound(int[] arr, int x) {
        int l = 0, r = arr.length;
        while (l < r) {
            int mid = (l + r) / 2;
            if (arr[mid] <= x) l = mid + 1;
            else r = mid;
        }
        return l;
    }
    
    private int lowerBound(int[] arr, int x) {
        int l = 0, r = arr.length;
        while (l < r) {
            int mid = (l + r) / 2;
            if (arr[mid] < x) l = mid + 1;
            else r = mid;
        }
        return l;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
class Solution:
    def fullBloomFlowers(self, flowers: List[List[int]], people: List[int]) -> List[int]:
        starts = sorted(f[0] for f in flowers)
        ends = sorted(f[1] for f in flowers)
        
        ans = []
        for p in people:
            bloom_count = bisect.bisect_right(starts, p) - bisect.bisect_left(ends, p)
            ans.append(bloom_count)
        
        return ans

Complexity

⏰ Time complexity: O(m log m + n log m).
- Sorting starts and ends arrays: O(m log m) where m is the number of flowers.
- Querying each p with binary search in sorted arrays: O(n log m) where n is the number of people.
🧺 Space complexity: O(m + n)
- O(m) for starts, ends arrays.
- O(n) for ans result array.
- Total: O(m + n).

Problem#

Examples#

Solution#

Method 1 - Using Binary Search#

Approach#

Code#

Complexity#