Number of Nodes With Value One

Problem

There is an undirected connected tree with n nodes labeled from 1 to n and n - 1 edges. You are given the integer n. The parent node of a node with a label v is the node with the label floor (v / 2). The root of the tree is the node with the label 1.

• For example, if n = 7, then the node with the label 3 has the node with the label floor(3 / 2) = 1 as its parent, and the node with the label 7 has the node with the label floor(7 / 2) = 3 as its parent.

You are also given an integer array queries. Initially, every node has a value 0 on it. For each query queries[i], you should flip all values in the subtree of the node with the label queries[i].

Return the total number of nodes with the value1 after processing all the queries.

Note that:

• Flipping the value of a node means that the node with the value 0 becomes 1 and vice versa.
• floor(x) is equivalent to rounding x down to the nearest integer.

Examples

Example 1:

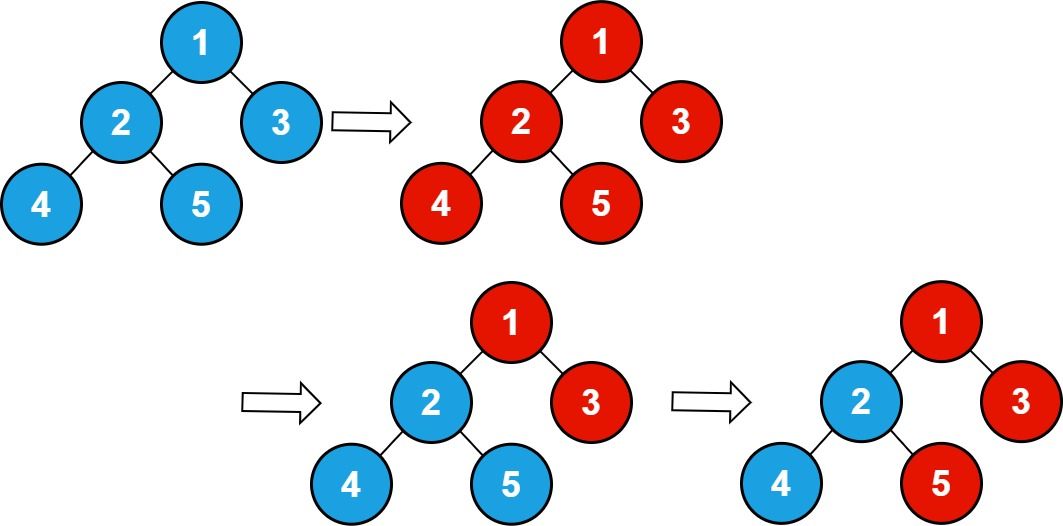
Input: n = 5 , queries = [1,2,5]
Output: 3
Explanation: The diagram above shows the tree structure and its status after performing the queries. The blue node represents the value 0, and the red node represents the value 1.
After processing the queries, there are three red nodes (nodes with value 1): 1, 3, and 5.

Example 2:

Input: n = 3, queries = [2,3,3]
Output: 1
Explanation: The diagram above shows the tree structure and its status after performing the queries. The blue node represents the value 0, and the red node represents the value 1.
After processing the queries, there are one red node (node with value 1): 2.

Constraints:

• 1 <= n <= 10^5
• 1 <= queries.length <= 10^5
• 1 <= queries[i] <= n

Solution

Method 1 – Difference Array for Range Flips

Intuition

Each query flips all values in the subtree of a node. The tree is a binary heap, so the subtree of node v is all nodes with labels in [v, r], where r is the largest label in v's subtree. We can use a difference array to efficiently process range flips, then count the number of nodes with odd flips.

Approach

1. For each query, compute the range [v, r] for the subtree rooted at v. For a binary heap, r = min(n, v * 2^{h} - 1), where h is the height such that v * 2^{h} <= n < v * 2^{h+1}.
2. Use a difference array to mark flips: diff[v] += 1, diff[r+1] -= 1.
3. After all queries, compute prefix sums and count nodes with odd flips.

Code

C++

#include <vector>
#include <cmath>
using namespace std;
class Solution {
public:
    int numberOfNodes(int n, vector<int>& queries) {
        vector<int> diff(n+2, 0);
        for (int v : queries) {
            int r = v;
            while (r*2 <= n) r = r*2;
            while (r*2+1 <= n) r = r*2+1;
            diff[v]++;
            if (r+1 <= n) diff[r+1]--;
        }
        int ans = 0, cur = 0;
        for (int i = 1; i <= n; ++i) {
            cur += diff[i];
            if (cur % 2 == 1) ++ans;
        }
        return ans;
    }
};

Go

func numberOfNodes(n int, queries []int) int {
    diff := make([]int, n+2)
    for _, v := range queries {
        r := v
        for r*2 <= n { r = r*2 }
        for r*2+1 <= n { r = r*2+1 }
        diff[v]++
        if r+1 <= n { diff[r+1]-- }
    }
    ans, cur := 0, 0
    for i := 1; i <= n; i++ {
        cur += diff[i]
        if cur%2 == 1 { ans++ }
    }
    return ans
}

Java

class Solution {
    public int numberOfNodes(int n, int[] queries) {
        int[] diff = new int[n+2];
        for (int v : queries) {
            int r = v;
            while (r*2 <= n) r = r*2;
            while (r*2+1 <= n) r = r*2+1;
            diff[v]++;
            if (r+1 <= n) diff[r+1]--;
        }
        int ans = 0, cur = 0;
        for (int i = 1; i <= n; ++i) {
            cur += diff[i];
            if (cur % 2 == 1) ans++;
        }
        return ans;
    }
}

Kotlin

class Solution {
    fun numberOfNodes(n: Int, queries: IntArray): Int {
        val diff = IntArray(n+2)
        for (v in queries) {
            var r = v
            while (r*2 <= n) r *= 2
            while (r*2+1 <= n) r = r*2+1
            diff[v]++
            if (r+1 <= n) diff[r+1]--
        }
        var ans = 0; var cur = 0
        for (i in 1..n) {
            cur += diff[i]
            if (cur % 2 == 1) ans++
        }
        return ans
    }
}

Python

class Solution:
    def numberOfNodes(self, n: int, queries: list[int]) -> int:
        diff = [0]*(n+2)
        for v in queries:
            r = v
            while r*2 <= n: r = r*2
            while r*2+1 <= n: r = r*2+1
            diff[v] += 1
            if r+1 <= n: diff[r+1] -= 1
        ans = cur = 0
        for i in range(1, n+1):
            cur += diff[i]
            if cur % 2 == 1: ans += 1
        return ans

Rust

impl Solution {
    pub fn number_of_nodes(n: i32, queries: Vec<i32>) -> i32 {
        let n = n as usize;
        let mut diff = vec![0; n+2];
        for &v in &queries {
            let mut r = v as usize;
            while r*2 <= n { r *= 2; }
            while r*2+1 <= n { r = r*2+1; }
            diff[v as usize] += 1;
            if r+1 <= n { diff[r+1] -= 1; }
        }
        let mut ans = 0;
        let mut cur = 0;
        for i in 1..=n {
            cur += diff[i];
            if cur % 2 == 1 { ans += 1; }
        }
        ans
    }
}

TypeScript

class Solution {
    numberOfNodes(n: number, queries: number[]): number {
        const diff = Array(n+2).fill(0);
        for (let v of queries) {
            let r = v;
            while (r*2 <= n) r = r*2;
            while (r*2+1 <= n) r = r*2+1;
            diff[v]++;
            if (r+1 <= n) diff[r+1]--;
        }
        let ans = 0, cur = 0;
        for (let i = 1; i <= n; ++i) {
            cur += diff[i];
            if (cur % 2 === 1) ans++;
        }
        return ans;
    }
}

Complexity

• ⏰ Time complexity: O(q log n + n), where q is the number of queries (to find subtree range) and n is the number of nodes.
• 🧺 Space complexity: O(n), for the difference array.