problemmediumalgorithmsleetcode-1319leetcode 1319leetcode1319

Number of Operations to Make Network Connected

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

There are n computers numbered from 0 to n - 1 connected by ethernet cables connections forming a network where connections[i] = [ai, bi] represents a connection between computers ai and bi. Any computer can reach any other computer directly or indirectly through the network.

You are given an initial computer network connections. You can extract certain cables between two directly connected computers, and place them between any pair of disconnected computers to make them directly connected.

Return the minimum number of times you need to do this in order to make all the computers connected. If it is not possible, return -1.

Examples

Example 1:

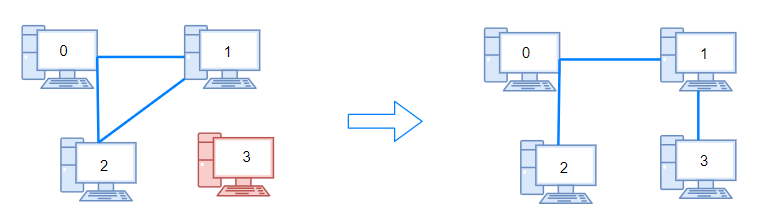
Input:
n = 4, connections = [[0,1],[0,2],[1,2]]
Output:
 1
Explanation: Remove cable between computer 1 and 2 and place between computers 1 and 3.

Example 2:

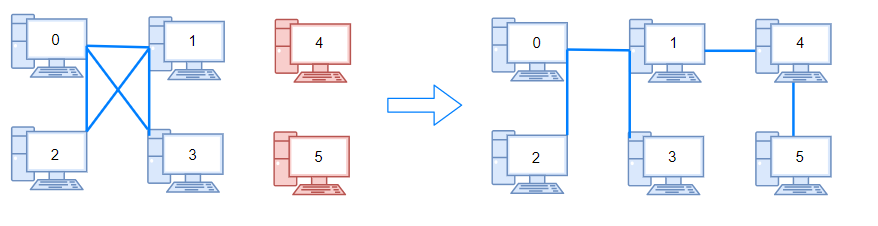
Input:
n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
Output:
 2

Example 3:

Input:
n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]
Output:
 -1
Explanation: There are not enough cables.

Solution

Method 1 – Union-Find (Disjoint Set Union)

Intuition

The key idea is to count the number of connected components in the network. To connect all computers, we need at least n-1 cables. If there are enough cables, the answer is the number of components minus one (the number of operations needed to connect all components).

Approach

  1. If the number of connections is less than n-1, return -1 (not enough cables).
  2. Initialize a Union-Find structure for all computers.
  3. For each connection, union the two computers.
  4. Count the number of connected components.
  5. The answer is the number of components minus one.

Code

C++
class Solution {
public:
    int makeConnected(int n, vector<vector<int>>& connections) {
        if (connections.size() < n - 1) return -1;
        vector<int> par(n);
        iota(par.begin(), par.end(), 0);
        function<int(int)> find = [&](int x) { return par[x] == x ? x : par[x] = find(par[x]); };
        for (auto& e : connections) par[find(e[0])] = find(e[1]);
        int comp = 0;
        for (int i = 0; i < n; ++i) if (find(i) == i) comp++;
        return comp - 1;
    }
};
Go
func makeConnected(n int, connections [][]int) int {
    if len(connections) < n-1 {
        return -1
    }
    par := make([]int, n)
    for i := range par { par[i] = i }
    var find func(int) int
    find = func(x int) int { if par[x] != x { par[x] = find(par[x]) }; return par[x] }
    for _, e := range connections {
        par[find(e[0])] = find(e[1])
    }
    comp := 0
    for i := 0; i < n; i++ {
        if find(i) == i {
            comp++
        }
    }
    return comp - 1
}
Java
class Solution {
    public int makeConnected(int n, int[][] connections) {
        if (connections.length < n - 1) return -1;
        int[] par = new int[n];
        for (int i = 0; i < n; i++) par[i] = i;
        java.util.function.IntUnaryOperator find = new java.util.function.IntUnaryOperator() {
            public int applyAsInt(int x) { return par[x] == x ? x : (par[x] = applyAsInt(par[x])); }
        };
        for (int[] e : connections) par[find.applyAsInt(e[0])] = find.applyAsInt(e[1]);
        int comp = 0;
        for (int i = 0; i < n; i++) if (find.applyAsInt(i) == i) comp++;
        return comp - 1;
    }
}
Kotlin
class Solution {
    fun makeConnected(n: Int, connections: Array<IntArray>): Int {
        if (connections.size < n - 1) return -1
        val par = IntArray(n) { it }
        fun find(x: Int): Int = if (par[x] == x) x else { par[x] = find(par[x]); par[x] }
        for (e in connections) par[find(e[0])] = find(e[1])
        var comp = 0
        for (i in 0 until n) if (find(i) == i) comp++
        return comp - 1
    }
}
Python
class Solution:
    def makeConnected(self, n: int, connections: list[list[int]]) -> int:
        if len(connections) < n - 1:
            return -1
        par = list(range(n))
        def find(x):
            if par[x] != x:
                par[x] = find(par[x])
            return par[x]
        for u, v in connections:
            par[find(u)] = find(v)
        comp = sum(find(i) == i for i in range(n))
        return comp - 1
Rust
impl Solution {
    pub fn make_connected(n: i32, connections: Vec<Vec<i32>>) -> i32 {
        let n = n as usize;
        if connections.len() < n - 1 { return -1; }
        let mut par: Vec<_> = (0..n).collect();
        fn find(par: &mut Vec<usize>, x: usize) -> usize {
            if par[x] != x { par[x] = find(par, par[x]); }
            par[x]
        }
        for e in &connections {
            let (u, v) = (e[0] as usize, e[1] as usize);
            let pu = find(&mut par, u);
            let pv = find(&mut par, v);
            par[pu] = pv;
        }
        let mut comp = 0;
        for i in 0..n {
            if find(&mut par, i) == i {
                comp += 1;
            }
        }
        (comp - 1) as i32
    }
}
TypeScript
class Solution {
    makeConnected(n: number, connections: number[][]): number {
        if (connections.length < n - 1) return -1;
        const par = Array.from({length: n}, (_, i) => i);
        const find = (x: number): number => par[x] === x ? x : (par[x] = find(par[x]));
        for (const [u, v] of connections) par[find(u)] = find(v);
        let comp = 0;
        for (let i = 0; i < n; i++) if (find(i) === i) comp++;
        return comp - 1;
    }
}

Complexity

  • ⏰ Time complexity: O(n + m), where n is the number of computers and m is the number of connections; each node and edge is processed once.
  • 🧺 Space complexity: O(n), for the parent array.

Comments