Number of paths from source to destination in a directed acyclic graph

Problem

Given a directed acyclic graph (DAG) with n vertices and m edges, find the number of different paths from a given source vertex to a destination vertex.

Examples

Example 1

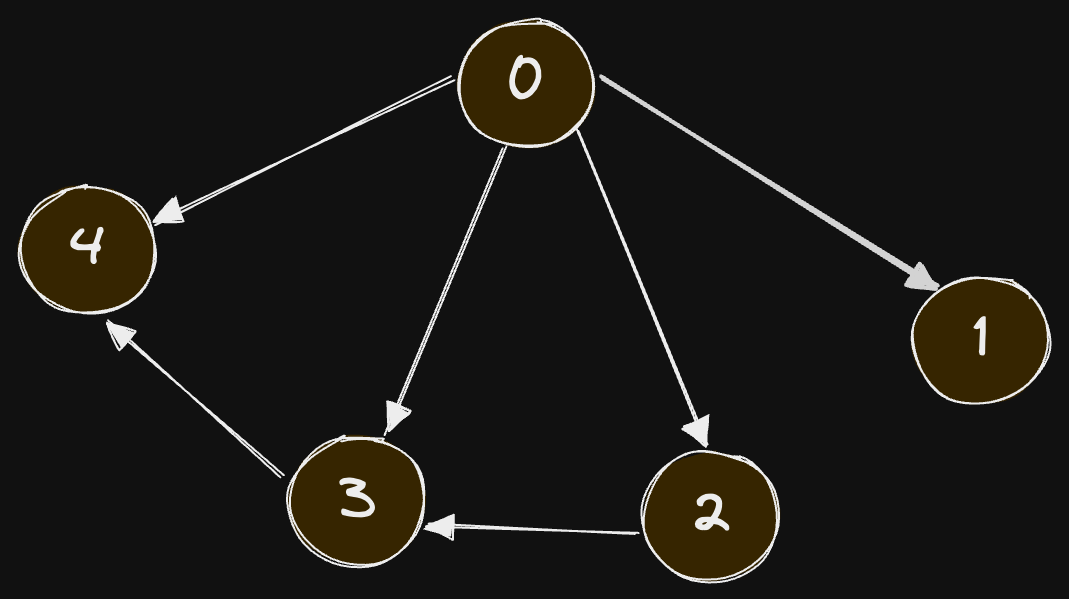
Input:
n = 5
edges = [
  [0, 2],
  [0, 3],
  [0, 4],
  [2, 3],
  [3, 4]
]
source = 0
destination = 4
Output: 3
Explanation:
0 -> 2 -> 3 -> 4
0 -> 3 -> 4
0 -> 4

Example 2

Input:
n = 2
edges = [
  [0, 1]
]
source = 0
destination = 1
Output: 1
Explanation: There exists only one path 0->1

Solution

Method 1 – Dynamic Programming with Topological Sort

Intuition

In a DAG, the number of paths from a node to the destination is the sum of the number of paths from each of its neighbors to the destination. By processing nodes in reverse topological order, we can compute the number of paths efficiently using dynamic programming.

Approach

1. Perform a topological sort of the DAG.
2. Initialize dp[dest] = 1 (only one way to reach destination from itself).
3. Traverse nodes in reverse topological order:

• For each node u, set dp[u] = sum of dp[v] for all neighbors v of u.

4. The answer is dp[source].

Code

C++

class Solution {
public:
  int countPaths(int n, vector<vector<int>>& edges, int source, int dest) {
    vector<vector<int>> adj(n);
    vector<int> indeg(n, 0);
    for (auto& e : edges) {
      adj[e[0]].push_back(e[1]);
      indeg[e[1]]++;
    }
    // Topological sort
    queue<int> q;
    for (int i = 0; i < n; ++i) if (indeg[i] == 0) q.push(i);
    vector<int> topo;
    while (!q.empty()) {
      int u = q.front(); q.pop();
      topo.push_back(u);
      for (int v : adj[u]) if (--indeg[v] == 0) q.push(v);
    }
    vector<int> dp(n, 0);
    dp[dest] = 1;
    for (int i = n-1; i >= 0; --i) {
      int u = topo[i];
      for (int v : adj[u]) dp[u] += dp[v];
    }
    return dp[source];
  }
};

Java

class Solution {
  public int countPaths(int n, int[][] edges, int source, int dest) {
    List<List<Integer>> adj = new ArrayList<>();
    int[] indeg = new int[n];
    for (int i = 0; i < n; ++i) adj.add(new ArrayList<>());
    for (int[] e : edges) {
      adj.get(e[0]).add(e[1]);
      indeg[e[1]]++;
    }
    Queue<Integer> q = new LinkedList<>();
    for (int i = 0; i < n; ++i) if (indeg[i] == 0) q.add(i);
    List<Integer> topo = new ArrayList<>();
    while (!q.isEmpty()) {
      int u = q.poll();
      topo.add(u);
      for (int v : adj.get(u)) if (--indeg[v] == 0) q.add(v);
    }
    int[] dp = new int[n];
    dp[dest] = 1;
    for (int i = n-1; i >= 0; --i) {
      int u = topo.get(i);
      for (int v : adj.get(u)) dp[u] += dp[v];
    }
    return dp[source];
  }
}

Python

class Solution:
  def count_paths(self, n: int, edges: list[list[int]], source: int, dest: int) -> int:
    from collections import deque, defaultdict
    adj = defaultdict(list)
    indeg = [0] * n
    for u, v in edges:
      adj[u].append(v)
      indeg[v] += 1
    q = deque([i for i in range(n) if indeg[i] == 0])
    topo = []
    while q:
      u = q.popleft()
      topo.append(u)
      for v in adj[u]:
        indeg[v] -= 1
        if indeg[v] == 0:
          q.append(v)
    dp = [0] * n
    dp[dest] = 1
    for u in reversed(topo):
      for v in adj[u]:
        dp[u] += dp[v]
    return dp[source]

Complexity

• ⏰ Time complexity: O(n + m), where n is the number of nodes and m is the number of edges. Each node and edge is processed once.
• 🧺 Space complexity: O(n + m), for adjacency list, indegree array, and dp array.