Problem

You are given an m x n 0-indexed 2D array of positive integers heights where heights[i][j] is the height of the person standing at position (i, j).

A person standing at position (row1, col1) can see a person standing at position (row2, col2) if:

  • The person at (row2, col2) is to the right or below the person at (row1, col1). More formally, this means that either row1 == row2 and col1 < col2 or row1 < row2 and col1 == col2.
  • Everyone in between them is shorter than both of them.

Return anm x n 2D array of integersanswer whereanswer[i][j]is the number of people that the person at position(i, j)can see.

Examples

Example 1:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2200-2299/2282.Number%20of%20People%20That%20Can%20Be%20Seen%20in%20a%20Grid/images/image-20220524180458-1.png)
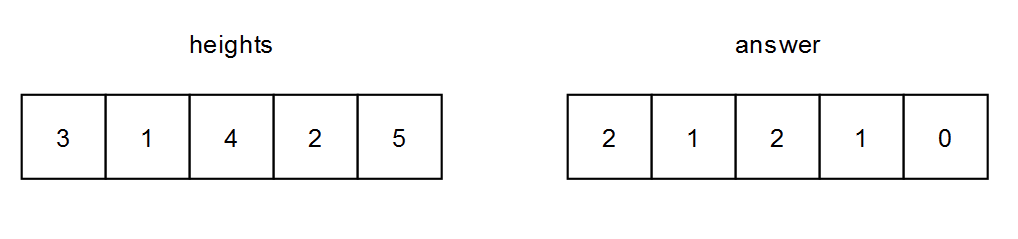
Input: heights = [[3,1,4,2,5]]
Output: [[2,1,2,1,0]]
Explanation:
- The person at (0, 0) can see the people at (0, 1) and (0, 2).
Note that he cannot see the person at (0, 4) because the person at (0, 2) is taller than him.
- The person at (0, 1) can see the person at (0, 2).
- The person at (0, 2) can see the people at (0, 3) and (0, 4).
- The person at (0, 3) can see the person at (0, 4).
- The person at (0, 4) cannot see anybody.

Example 2:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2200-2299/2282.Number%20of%20People%20That%20Can%20Be%20Seen%20in%20a%20Grid/images/image-20220523113533-2.png)
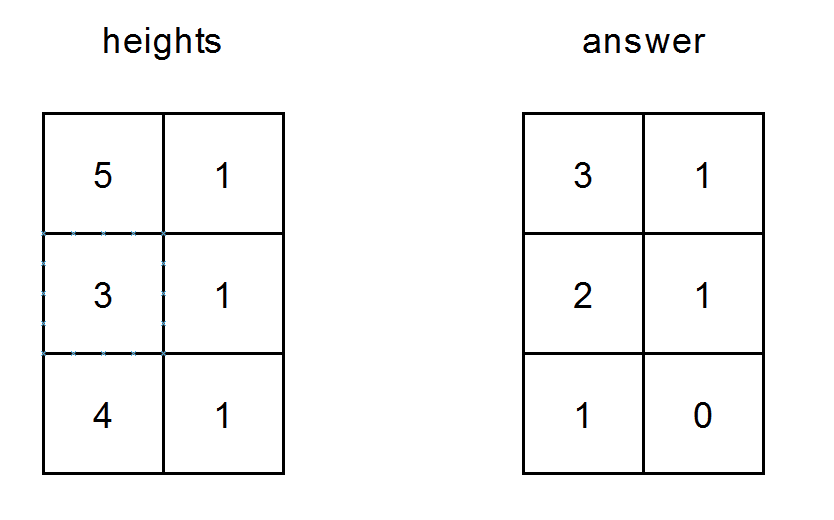
Input: heights = [[5,1],[3,1],[4,1]]
Output: [[3,1],[2,1],[1,0]]
Explanation:
- The person at (0, 0) can see the people at (0, 1), (1, 0) and (2, 0).
- The person at (0, 1) can see the person at (1, 1).
- The person at (1, 0) can see the people at (1, 1) and (2, 0).
- The person at (1, 1) can see the person at (2, 1).
- The person at (2, 0) can see the person at (2, 1).
- The person at (2, 1) cannot see anybody.

Constraints:

  • 1 <= heights.length <= 400
  • 1 <= heights[i].length <= 400
  • 1 <= heights[i][j] <= 10^5

Solution

Method 1 – Monotonic Stack for Each Row and Column

Intuition

For each person, we need to count how many people they can see to the right and below, following the rule that all people in between must be shorter than both. This is a classic monotonic stack problem, similar to “next greater element” but counting visible people.

Approach

  1. For each row, process from right to left using a stack:
    • For each person, pop from the stack while the top is shorter than the current person, counting each pop as a visible person.
    • If the stack is not empty after popping, the next person is also visible.
  2. Repeat for each column, processing from bottom to top.
  3. Sum the counts for each person.
  4. Return the answer grid.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

#include <vector>
#include <stack>
using namespace std;
class Solution {
public:
    vector<vector<int>> canSeePersons(vector<vector<int>>& heights) {
        int m = heights.size(), n = heights[0].size();
        vector<vector<int>> ans(m, vector<int>(n, 0));
        // Right direction
        for (int i = 0; i < m; ++i) {
            stack<int> st;
            for (int j = n-1; j >= 0; --j) {
                int cnt = 0;
                while (!st.empty() && heights[i][j] > heights[i][st.top()]) {
                    st.pop(); ++cnt;
                }
                if (!st.empty()) ++cnt;
                ans[i][j] += cnt;
                st.push(j);
            }
        }
        // Down direction
        for (int j = 0; j < n; ++j) {
            stack<int> st;
            for (int i = m-1; i >= 0; --i) {
                int cnt = 0;
                while (!st.empty() && heights[i][j] > heights[st.top()][j]) {
                    st.pop(); ++cnt;
                }
                if (!st.empty()) ++cnt;
                ans[i][j] += cnt;
                st.push(i);
            }
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

func canSeePersons(heights [][]int) [][]int {
    m, n := len(heights), len(heights[0])
    ans := make([][]int, m)
    for i := range ans { ans[i] = make([]int, n) }
    // Right direction
    for i := 0; i < m; i++ {
        st := []int{}
        for j := n-1; j >= 0; j-- {
            cnt := 0
            for len(st) > 0 && heights[i][j] > heights[i][st[len(st)-1]] {
                st = st[:len(st)-1]; cnt++
            }
            if len(st) > 0 { cnt++ }
            ans[i][j] += cnt
            st = append(st, j)
        }
    }
    // Down direction
    for j := 0; j < n; j++ {
        st := []int{}
        for i := m-1; i >= 0; i-- {
            cnt := 0
            for len(st) > 0 && heights[i][j] > heights[st[len(st)-1]][j] {
                st = st[:len(st)-1]; cnt++
            }
            if len(st) > 0 { cnt++ }
            ans[i][j] += cnt
            st = append(st, i)
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

import java.util.*;
class Solution {
    public int[][] canSeePersons(int[][] heights) {
        int m = heights.length, n = heights[0].length;
        int[][] ans = new int[m][n];
        // Right direction
        for (int i = 0; i < m; ++i) {
            Deque<Integer> st = new ArrayDeque<>();
            for (int j = n-1; j >= 0; --j) {
                int cnt = 0;
                while (!st.isEmpty() && heights[i][j] > heights[i][st.peek()]) {
                    st.pop(); ++cnt;
                }
                if (!st.isEmpty()) ++cnt;
                ans[i][j] += cnt;
                st.push(j);
            }
        }
        // Down direction
        for (int j = 0; j < n; ++j) {
            Deque<Integer> st = new ArrayDeque<>();
            for (int i = m-1; i >= 0; --i) {
                int cnt = 0;
                while (!st.isEmpty() && heights[i][j] > heights[st.peek()][j]) {
                    st.pop(); ++cnt;
                }
                if (!st.isEmpty()) ++cnt;
                ans[i][j] += cnt;
                st.push(i);
            }
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class Solution {
    fun canSeePersons(heights: Array<IntArray>): Array<IntArray> {
        val m = heights.size
        val n = heights[0].size
        val ans = Array(m) { IntArray(n) }
        // Right direction
        for (i in 0 until m) {
            val st = ArrayDeque<Int>()
            for (j in n-1 downTo 0) {
                var cnt = 0
                while (st.isNotEmpty() && heights[i][j] > heights[i][st.peek()]) {
                    st.pop(); cnt++
                }
                if (st.isNotEmpty()) cnt++
                ans[i][j] += cnt
                st.push(j)
            }
        }
        // Down direction
        for (j in 0 until n) {
            val st = ArrayDeque<Int>()
            for (i in m-1 downTo 0) {
                var cnt = 0
                while (st.isNotEmpty() && heights[i][j] > heights[st.peek()][j]) {
                    st.pop(); cnt++
                }
                if (st.isNotEmpty()) cnt++
                ans[i][j] += cnt
                st.push(i)
            }
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution:
    def canSeePersons(self, heights: list[list[int]]) -> list[list[int]]:
        m, n = len(heights), len(heights[0])
        ans = [[0]*n for _ in range(m)]
        # Right direction
        for i in range(m):
            st = []
            for j in range(n-1, -1, -1):
                cnt = 0
                while st and heights[i][j] > heights[i][st[-1]]:
                    st.pop(); cnt += 1
                if st: cnt += 1
                ans[i][j] += cnt
                st.append(j)
        # Down direction
        for j in range(n):
            st = []
            for i in range(m-1, -1, -1):
                cnt = 0
                while st and heights[i][j] > heights[st[-1]][j]:
                    st.pop(); cnt += 1
                if st: cnt += 1
                ans[i][j] += cnt
                st.append(i)
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

impl Solution {
    pub fn can_see_persons(heights: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
        let m = heights.len();
        let n = heights[0].len();
        let mut ans = vec![vec![0; n]; m];
        // Right direction
        for i in 0..m {
            let mut st = Vec::new();
            for j in (0..n).rev() {
                let mut cnt = 0;
                while let Some(&k) = st.last() {
                    if heights[i][j] > heights[i][k] {
                        st.pop(); cnt += 1;
                    } else { break; }
                }
                if !st.is_empty() { cnt += 1; }
                ans[i][j] += cnt;
                st.push(j);
            }
        }
        // Down direction
        for j in 0..n {
            let mut st = Vec::new();
            for i in (0..m).rev() {
                let mut cnt = 0;
                while let Some(&k) = st.last() {
                    if heights[i][j] > heights[k][j] {
                        st.pop(); cnt += 1;
                    } else { break; }
                }
                if !st.is_empty() { cnt += 1; }
                ans[i][j] += cnt;
                st.push(i);
            }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

class Solution {
    canSeePersons(heights: number[][]): number[][] {
        const m = heights.length, n = heights[0].length;
        const ans = Array.from({length:m},()=>Array(n).fill(0));
        // Right direction
        for (let i = 0; i < m; ++i) {
            const st: number[] = [];
            for (let j = n-1; j >= 0; --j) {
                let cnt = 0;
                while (st.length && heights[i][j] > heights[i][st[st.length-1]]) {
                    st.pop(); cnt++;
                }
                if (st.length) cnt++;
                ans[i][j] += cnt;
                st.push(j);
            }
        }
        // Down direction
        for (let j = 0; j < n; ++j) {
            const st: number[] = [];
            for (let i = m-1; i >= 0; --i) {
                let cnt = 0;
                while (st.length && heights[i][j] > heights[st[st.length-1]][j]) {
                    st.pop(); cnt++;
                }
                if (st.length) cnt++;
                ans[i][j] += cnt;
                st.push(i);
            }
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(m*n), where m and n are the grid dimensions. Each cell is processed twice with a stack.
  • 🧺 Space complexity: O(m*n), for the answer grid and stacks.