Problem

There is a company with n branches across the country, some of which are connected by roads. Initially, all branches are reachable from each other by traveling some roads.

The company has realized that they are spending an excessive amount of time traveling between their branches. As a result, they have decided to close down some of these branches (possibly none). However, they want to ensure that the remaining branches have a distance of at most maxDistance from each other.

The distance between two branches is the minimum total traveled length needed to reach one branch from another.

You are given integers n, maxDistance, and a 0-indexed 2D array roads, where roads[i] = [ui, vi, wi] represents the undirected road between branches ui and vi with length wi.

Return the number of possible sets of closing branches, so that any branch has a distance of at mostmaxDistance from any other.

Note that, after closing a branch, the company will no longer have access to any roads connected to it.

Note that, multiple roads are allowed.

Examples

Example 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


![](https://assets.leetcode.com/uploads/2023/11/08/example11.png)

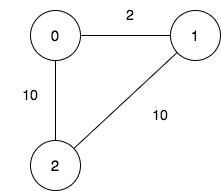
Input: n = 3, maxDistance = 5, roads = [[0,1,2],[1,2,10],[0,2,10]]
Output: 5
Explanation: The possible sets of closing branches are:
- The set [2], after closing, active branches are [0,1] and they are reachable to each other within distance 2.
- The set [0,1], after closing, the active branch is [2].
- The set [1,2], after closing, the active branch is [0].
- The set [0,2], after closing, the active branch is [1].
- The set [0,1,2], after closing, there are no active branches.
It can be proven, that there are only 5 possible sets of closing branches.

Example 2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


![](https://assets.leetcode.com/uploads/2023/11/08/example22.png)

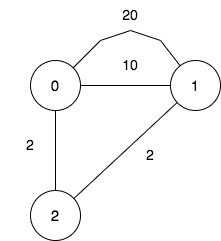
Input: n = 3, maxDistance = 5, roads = [[0,1,20],[0,1,10],[1,2,2],[0,2,2]]
Output: 7
Explanation: The possible sets of closing branches are:
- The set [], after closing, active branches are [0,1,2] and they are reachable to each other within distance 4.
- The set [0], after closing, active branches are [1,2] and they are reachable to each other within distance 2.
- The set [1], after closing, active branches are [0,2] and they are reachable to each other within distance 2.
- The set [0,1], after closing, the active branch is [2].
- The set [1,2], after closing, the active branch is [0].
- The set [0,2], after closing, the active branch is [1].
- The set [0,1,2], after closing, there are no active branches.
It can be proven, that there are only 7 possible sets of closing branches.

Example 3

1
2
3
4
5
6

Input: n = 1, maxDistance = 10, roads = []
Output: 2
Explanation: The possible sets of closing branches are:
- The set [], after closing, the active branch is [0].
- The set [0], after closing, there are no active branches.
It can be proven, that there are only 2 possible sets of closing branches.

Constraints

  • 1 <= n <= 10
  • 1 <= maxDistance <= 10^5
  • 0 <= roads.length <= 1000
  • roads[i].length == 3
  • 0 <= ui, vi <= n - 1
  • ui != vi
  • 1 <= wi <= 1000
  • All branches are reachable from each other by traveling some roads.

Solution

Method 1 – Bitmask Enumeration and Floyd-Warshall

Intuition

Since n is small (≤10), we can enumerate all possible sets of closing branches using bitmasks. For each set, we compute the shortest paths between remaining branches using Floyd-Warshall, and check if all pairs are within maxDistance.

Approach

  1. For each bitmask (subset of branches to keep open), build the graph with only those branches.
  2. For each subset, run Floyd-Warshall to compute shortest paths between all pairs of open branches.
  3. If all pairs are reachable and have distance ≤ maxDistance, count this subset as valid.
  4. Return the total count.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
    int possibleSets(int n, int maxDistance, vector<vector<int>>& roads) {
        vector<vector<int>> g(n, vector<int>(n, 1e9));
        for (int i = 0; i < n; ++i) g[i][i] = 0;
        for (auto& r : roads) {
            g[r[0]][r[1]] = min(g[r[0]][r[1]], r[2]);
            g[r[1]][r[0]] = min(g[r[1]][r[0]], r[2]);
        }
        int ans = 0;
        for (int mask = 0; mask < (1<<n); ++mask) {
            vector<vector<int>> dist = g;
            for (int k = 0; k < n; ++k) if (mask & (1<<k))
                for (int i = 0; i < n; ++i) for (int j = 0; j < n; ++j)
                    dist[i][k] = dist[k][j] = dist[i][j] = 1e9;
            for (int k = 0; k < n; ++k) if (!(mask & (1<<k)))
                for (int i = 0; i < n; ++i) if (!(mask & (1<<i)))
                    for (int j = 0; j < n; ++j) if (!(mask & (1<<j)))
                        dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
            bool ok = true;
            vector<int> active;
            for (int i = 0; i < n; ++i) if (!(mask & (1<<i))) active.push_back(i);
            for (int i : active) for (int j : active) if (i != j)
                if (dist[i][j] > maxDistance) ok = false;
            if (ok) ++ans;
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

func possibleSets(n int, maxDistance int, roads [][]int) int {
    g := make([][]int, n)
    for i := range g {
        g[i] = make([]int, n)
        for j := range g[i] {
            if i == j {
                g[i][j] = 0
            } else {
                g[i][j] = 1e9
            }
        }
    }
    for _, r := range roads {
        u, v, w := r[0], r[1], r[2]
        if w < g[u][v] { g[u][v] = w }
        if w < g[v][u] { g[v][u] = w }
    }
    ans := 0
    for mask := 0; mask < 1<<n; mask++ {
        dist := make([][]int, n)
        for i := range dist {
            dist[i] = make([]int, n)
            copy(dist[i], g[i])
        }
        for k := 0; k < n; k++ {
            if mask&(1<<k) != 0 {
                for i := 0; i < n; i++ {
                    dist[i][k] = 1e9
                    dist[k][i] = 1e9
                }
            }
        }
        for k := 0; k < n; k++ {
            if mask&(1<<k) == 0 {
                for i := 0; i < n; i++ {
                    if mask&(1<<i) == 0 {
                        for j := 0; j < n; j++ {
                            if mask&(1<<j) == 0 {
                                if dist[i][j] > dist[i][k]+dist[k][j] {
                                    dist[i][j] = dist[i][k]+dist[k][j]
                                }
                            }
                        }
                    }
                }
            }
        }
        ok := true
        active := []int{}
        for i := 0; i < n; i++ {
            if mask&(1<<i) == 0 {
                active = append(active, i)
            }
        }
        for _, i := range active {
            for _, j := range active {
                if i != j && dist[i][j] > maxDistance {
                    ok = false
                }
            }
        }
        if ok { ans++ }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
    public int possibleSets(int n, int maxDistance, int[][] roads) {
        int[][] g = new int[n][n];
        for (int i = 0; i < n; ++i) for (int j = 0; j < n; ++j) g[i][j] = i==j?0:1000000000;
        for (int[] r : roads) {
            g[r[0]][r[1]] = Math.min(g[r[0]][r[1]], r[2]);
            g[r[1]][r[0]] = Math.min(g[r[1]][r[0]], r[2]);
        }
        int ans = 0;
        for (int mask = 0; mask < (1<<n); ++mask) {
            int[][] dist = new int[n][n];
            for (int i = 0; i < n; ++i) dist[i] = g[i].clone();
            for (int k = 0; k < n; ++k) if ((mask & (1<<k)) != 0)
                for (int i = 0; i < n; ++i) dist[i][k] = dist[k][i] = 1000000000;
            for (int k = 0; k < n; ++k) if ((mask & (1<<k)) == 0)
                for (int i = 0; i < n; ++i) if ((mask & (1<<i)) == 0)
                    for (int j = 0; j < n; ++j) if ((mask & (1<<j)) == 0)
                        dist[i][j] = Math.min(dist[i][j], dist[i][k]+dist[k][j]);
            boolean ok = true;
            for (int i = 0; i < n; ++i) if ((mask & (1<<i)) == 0)
                for (int j = 0; j < n; ++j) if (i != j && (mask & (1<<j)) == 0)
                    if (dist[i][j] > maxDistance) ok = false;
            if (ok) ++ans;
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
    fun possibleSets(n: Int, maxDistance: Int, roads: Array<IntArray>): Int {
        val g = Array(n) { IntArray(n) { if (it == 0) 0 else 1000000000 } }
        for (i in 0 until n) g[i][i] = 0
        for (r in roads) {
            g[r[0]][r[1]] = minOf(g[r[0]][r[1]], r[2])
            g[r[1]][r[0]] = minOf(g[r[1]][r[0]], r[2])
        }
        var ans = 0
        for (mask in 0 until (1 shl n)) {
            val dist = Array(n) { g[it].clone() }
            for (k in 0 until n) if ((mask and (1 shl k)) != 0)
                for (i in 0 until n) dist[i][k] = dist[k][i] = 1000000000
            for (k in 0 until n) if ((mask and (1 shl k)) == 0)
                for (i in 0 until n) if ((mask and (1 shl i)) == 0)
                    for (j in 0 until n) if ((mask and (1 shl j)) == 0)
                        dist[i][j] = minOf(dist[i][j], dist[i][k]+dist[k][j])
            var ok = true
            for (i in 0 until n) if ((mask and (1 shl i)) == 0)
                for (j in 0 until n) if (i != j && (mask and (1 shl j)) == 0)
                    if (dist[i][j] > maxDistance) ok = false
            if (ok) ans++
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class Solution:
    def possibleSets(self, n: int, maxDistance: int, roads: list[list[int]]) -> int:
        g = [[float('inf')]*n for _ in range(n)]
        for i in range(n): g[i][i] = 0
        for u,v,w in roads:
            g[u][v] = min(g[u][v], w)
            g[v][u] = min(g[v][u], w)
        ans = 0
        for mask in range(1<<n):
            dist = [row[:] for row in g]
            for k in range(n):
                if mask & (1<<k):
                    for i in range(n): dist[i][k] = dist[k][i] = float('inf')
            for k in range(n):
                if not (mask & (1<<k)):
                    for i in range(n):
                        if not (mask & (1<<i)):
                            for j in range(n):
                                if not (mask & (1<<j)):
                                    dist[i][j] = min(dist[i][j], dist[i][k]+dist[k][j])
            ok = True
            active = [i for i in range(n) if not (mask & (1<<i))]
            for i in active:
                for j in active:
                    if i != j and dist[i][j] > maxDistance:
                        ok = False
            if ok: ans += 1
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

impl Solution {
    pub fn possible_sets(n: i32, max_distance: i32, roads: Vec<Vec<i32>>) -> i32 {
        let n = n as usize;
        let mut g = vec![vec![1_000_000_000; n]; n];
        for i in 0..n { g[i][i] = 0; }
        for r in &roads {
            let u = r[0] as usize;
            let v = r[1] as usize;
            let w = r[2];
            g[u][v] = g[u][v].min(w);
            g[v][u] = g[v][u].min(w);
        }
        let mut ans = 0;
        for mask in 0..(1<<n) {
            let mut dist = g.clone();
            for k in 0..n {
                if (mask & (1<<k)) != 0 {
                    for i in 0..n { dist[i][k] = 1_000_000_000; dist[k][i] = 1_000_000_000; }
                }
            }
            for k in 0..n {
                if (mask & (1<<k)) == 0 {
                    for i in 0..n {
                        if (mask & (1<<i)) == 0 {
                            for j in 0..n {
                                if (mask & (1<<j)) == 0 {
                                    let d = dist[i][k] + dist[k][j];
                                    if dist[i][j] > d { dist[i][j] = d; }
                                }
                            }
                        }
                    }
                }
            }
            let mut ok = true;
            let active: Vec<_> = (0..n).filter(|&i| (mask & (1<<i)) == 0).collect();
            for &i in &active {
                for &j in &active {
                    if i != j && dist[i][j] > max_distance { ok = false; }
                }
            }
            if ok { ans += 1; }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
    possibleSets(n: number, maxDistance: number, roads: number[][]): number {
        const g = Array.from({length:n},()=>Array(n).fill(1e9));
        for (let i = 0; i < n; ++i) g[i][i] = 0;
        for (const [u,v,w] of roads) {
            g[u][v] = Math.min(g[u][v], w);
            g[v][u] = Math.min(g[v][u], w);
        }
        let ans = 0;
        for (let mask = 0; mask < (1<<n); ++mask) {
            const dist = g.map(row=>row.slice());
            for (let k = 0; k < n; ++k) if (mask & (1<<k))
                for (let i = 0; i < n; ++i) dist[i][k] = dist[k][i] = 1e9;
            for (let k = 0; k < n; ++k) if (!(mask & (1<<k)))
                for (let i = 0; i < n; ++i) if (!(mask & (1<<i)))
                    for (let j = 0; j < n; ++j) if (!(mask & (1<<j)))
                        dist[i][j] = Math.min(dist[i][j], dist[i][k]+dist[k][j]);
            let ok = true;
            const active = [];
            for (let i = 0; i < n; ++i) if (!(mask & (1<<i))) active.push(i);
            for (const i of active) for (const j of active) if (i !== j)
                if (dist[i][j] > maxDistance) ok = false;
            if (ok) ans++;
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(2^n * n^3), where n is the number of branches. For each subset, we run Floyd-Warshall on up to n nodes.
  • 🧺 Space complexity: O(n^2), for the distance matrix.