Number of Restricted Paths From First to Last Node Problem

Problem

There is an undirected weighted connected graph. You are given a positive integer n which denotes that the graph has n nodes labeled from 1 to n, and an array edges where each edges[i] = [ui, vi, weighti] denotes that there is an edge between nodes ui and vi with weight equal to weighti.

A path from node start to node end is a sequence of nodes [z0, z1, z2, ..., zk] such that z0 = start and zk = end and there is an edge between zi and zi+1 where 0 <= i <= k-1.

The distance of a path is the sum of the weights on the edges of the path. Let distanceToLastNode(x) denote the shortest distance of a path between node n and node x. A restricted path is a path that also satisfies that distanceToLastNode(zi) > distanceToLastNode(zi+1) where 0 <= i <= k-1.

Return the number of restricted paths from node 1 to node n. Since that number may be too large, return it modulo 109 + 7.

Examples

Example 1:

1
2
3
4
5
6
7
8


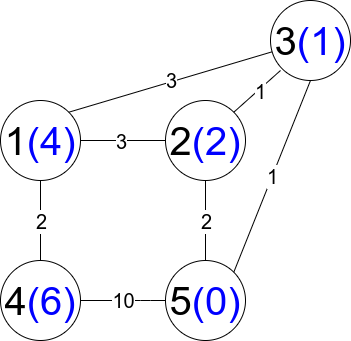
Input:
n = 5, edges = [[1,2,3],[1,3,3],[2,3,1],[1,4,2],[5,2,2],[3,5,1],[5,4,10]]
Output:
 3
Explanation: Each circle contains the node number in black and its `distanceToLastNode value in blue.` The three restricted paths are:
1) 1 --> 2 --> 5
2) 1 --> 2 --> 3 --> 5
3) 1 --> 3 --> 5

Example 2:

1
2
3
4
5


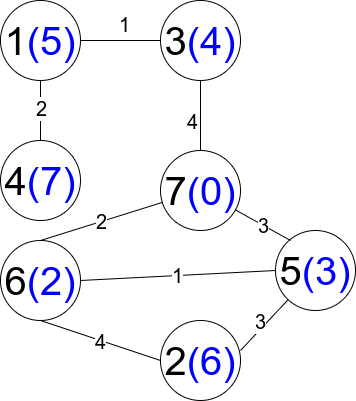
Input:
n = 7, edges = [[1,3,1],[4,1,2],[7,3,4],[2,5,3],[5,6,1],[6,7,2],[7,5,3],[2,6,4]]
Output:
 1
Explanation: Each circle contains the node number in black and its `distanceToLastNode value in blue.` The only restricted path is 1 --> 3 --> 7.

Solution

Method 1 – Dijkstra + DP

Intuition

The key idea is to use Dijkstra’s algorithm to compute the shortest distance from every node to node n. Then, use dynamic programming to count the number of restricted paths from node 1 to node n, where each step must go to a neighbor with a strictly smaller distance to node n.

Approach

Build the graph as an adjacency list.
Use Dijkstra’s algorithm from node n to compute the shortest distance from every node to node n.
Sort nodes by their distance to node n.
Use DP: for each node, sum the number of restricted paths from its neighbors with a strictly smaller distance.
The answer is the number of restricted paths from node 1 to node n.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38


class Solution {
public:
    int countRestrictedPaths(int n, vector<vector<int>>& edges) {
        const int MOD = 1e9+7;
        vector<vector<pair<int,int>>> g(n+1);
        for (auto& e : edges) {
            g[e[0]].emplace_back(e[1], e[2]);
            g[e[1]].emplace_back(e[0], e[2]);
        }
        vector<int> dist(n+1, INT_MAX);
        dist[n] = 0;
        priority_queue<pair<int,int>, vector<pair<int,int>>, greater<>> pq;
        pq.emplace(0, n);
        while (!pq.empty()) {
            auto [d, u] = pq.top(); pq.pop();
            if (d > dist[u]) continue;
            for (auto& [v, w] : g[u]) {
                if (dist[v] > d + w) {
                    dist[v] = d + w;
                    pq.emplace(dist[v], v);
                }
            }
        }
        vector<int> order(n);
        iota(order.begin(), order.end(), 1);
        sort(order.begin(), order.end(), [&](int a, int b) { return dist[a] < dist[b]; });
        vector<int> dp(n+1);
        dp[n] = 1;
        for (int u : order) {
            for (auto& [v, w] : g[u]) {
                if (dist[u] > dist[v]) {
                    dp[u] = (dp[u] + dp[v]) % MOD;
                }
            }
        }
        return dp[1];
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46


func countRestrictedPaths(n int, edges [][]int) int {
    const MOD = 1e9 + 7
    g := make([][][2]int, n+1)
    for _, e := range edges {
        g[e[0]] = append(g[e[0]], [2]int{e[1], e[2]})
        g[e[1]] = append(g[e[1]], [2]int{e[0], e[2]})
    }
    dist := make([]int, n+1)
    for i := range dist { dist[i] = 1<<31-1 }
    dist[n] = 0
    pq := &hp{}
    heap.Init(pq)
    heap.Push(pq, [2]int{0, n})
    for pq.Len() > 0 {
        d, u := (*pq)[0][0], (*pq)[0][1]
        heap.Pop(pq)
        if d > dist[u] { continue }
        for _, vw := range g[u] {
            v, w := vw[0], vw[1]
            if dist[v] > d+w {
                dist[v] = d + w
                heap.Push(pq, [2]int{dist[v], v})
            }
        }
    }
    order := make([]int, n)
    for i := 1; i <= n; i++ { order[i-1] = i }
    sort.Slice(order, func(i, j int) bool { return dist[order[i]] < dist[order[j]] })
    dp := make([]int, n+1)
    dp[n] = 1
    for _, u := range order {
        for _, vw := range g[u] {
            v := vw[0]
            if dist[u] > dist[v] {
                dp[u] = (dp[u] + dp[v]) % MOD
            }
        }
    }
    return dp[1]
}
type hp [][2]int
func (h hp) Len() int           { return len(h) }
func (h hp) Less(i, j int) bool { return h[i][0] < h[j][0] }
func (h hp) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(x interface{}) { *h = append(*h, x.([2]int)) }
func (h *hp) Pop() interface{}   { old := *h; x := old[len(old)-1]; *h = old[:len(old)-1]; return x }

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42


class Solution {
    public int countRestrictedPaths(int n, int[][] edges) {
        final int MOD = 1_000_000_007;
        List<int[]>[] g = new List[n+1];
        for (int i = 1; i <= n; i++) g[i] = new ArrayList<>();
        for (int[] e : edges) {
            g[e[0]].add(new int[]{e[1], e[2]});
            g[e[1]].add(new int[]{e[0], e[2]});
        }
        int[] dist = new int[n+1];
        Arrays.fill(dist, Integer.MAX_VALUE);
        dist[n] = 0;
        PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
        pq.offer(new int[]{0, n});
        while (!pq.isEmpty()) {
            int[] cur = pq.poll();
            int d = cur[0], u = cur[1];
            if (d > dist[u]) continue;
            for (int[] vw : g[u]) {
                int v = vw[0], w = vw[1];
                if (dist[v] > d + w) {
                    dist[v] = d + w;
                    pq.offer(new int[]{dist[v], v});
                }
            }
        }
        Integer[] order = new Integer[n];
        for (int i = 1; i <= n; i++) order[i-1] = i;
        Arrays.sort(order, Comparator.comparingInt(a -> dist[a]));
        int[] dp = new int[n+1];
        dp[n] = 1;
        for (int u : order) {
            for (int[] vw : g[u]) {
                int v = vw[0];
                if (dist[u] > dist[v]) {
                    dp[u] = (dp[u] + dp[v]) % MOD;
                }
            }
        }
        return dp[1];
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


class Solution {
    fun countRestrictedPaths(n: Int, edges: Array<IntArray>): Int {
        val MOD = 1_000_000_007
        val g = Array(n+1) { mutableListOf<Pair<Int,Int>>() }
        for (e in edges) {
            g[e[0]].add(e[1] to e[2])
            g[e[1]].add(e[0] to e[2])
        }
        val dist = IntArray(n+1) { Int.MAX_VALUE }
        dist[n] = 0
        val pq = java.util.PriorityQueue(compareBy<Pair<Int,Int>> { it.first })
        pq.add(0 to n)
        while (pq.isNotEmpty()) {
            val (d, u) = pq.remove()
            if (d > dist[u]) continue
            for ((v, w) in g[u]) {
                if (dist[v] > d + w) {
                    dist[v] = d + w
                    pq.add(dist[v] to v)
                }
            }
        }
        val order = (1..n).sortedBy { dist[it] }
        val dp = IntArray(n+1)
        dp[n] = 1
        for (u in order) {
            for ((v, _) in g[u]) {
                if (dist[u] > dist[v]) {
                    dp[u] = (dp[u] + dp[v]) % MOD
                }
            }
        }
        return dp[1]
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


class Solution:
    def countRestrictedPaths(self, n: int, edges: list[list[int]]) -> int:
        import heapq
        MOD = 10**9 + 7
        g = [[] for _ in range(n+1)]
        for u, v, w in edges:
            g[u].append((v, w))
            g[v].append((u, w))
        dist = [float('inf')] * (n+1)
        dist[n] = 0
        h = [(0, n)]
        while h:
            d, u = heapq.heappop(h)
            if d > dist[u]: continue
            for v, w in g[u]:
                if dist[v] > d + w:
                    dist[v] = d + w
                    heapq.heappush(h, (dist[v], v))
        order = sorted(range(1, n+1), key=lambda x: dist[x])
        dp = [0] * (n+1)
        dp[n] = 1
        for u in order:
            for v, _ in g[u]:
                if dist[u] > dist[v]:
                    dp[u] = (dp[u] + dp[v]) % MOD
        return dp[1]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37


impl Solution {
    pub fn count_restricted_paths(n: i32, edges: Vec<Vec<i32>>) -> i32 {
        use std::collections::BinaryHeap;
        let n = n as usize;
        let mut g = vec![vec![]; n+1];
        for e in &edges {
            g[e[0] as usize].push((e[1] as usize, e[2]));
            g[e[1] as usize].push((e[0] as usize, e[2]));
        }
        let mut dist = vec![i32::MAX; n+1];
        dist[n] = 0;
        let mut h = std::collections::BinaryHeap::new();
        h.push((0, n));
        while let Some((d, u)) = h.pop() {
            let d = -d;
            if d > dist[u] { continue; }
            for &(v, w) in &g[u] {
                if dist[v] > d + w {
                    dist[v] = d + w;
                    h.push((-(dist[v]), v));
                }
            }
        }
        let mut order: Vec<_> = (1..=n).collect();
        order.sort_by_key(|&x| dist[x]);
        let mut dp = vec![0; n+1];
        dp[n] = 1;
        for &u in &order {
            for &(v, _) in &g[u] {
                if dist[u] > dist[v] {
                    dp[u] = (dp[u] + dp[v]) % 1_000_000_007;
                }
            }
        }
        dp[1]
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


class Solution {
    countRestrictedPaths(n: number, edges: number[][]): number {
        const MOD = 1e9 + 7;
        const g: [number, number][][] = Array.from({length: n+1}, () => []);
        for (const [u, v, w] of edges) {
            g[u].push([v, w]);
            g[v].push([u, w]);
        }
        const dist = Array(n+1).fill(Infinity);
        dist[n] = 0;
        const h: [number, number][] = [[0, n]];
        while (h.length) {
            h.sort((a, b) => a[0] - b[0]);
            const [d, u] = h.shift()!;
            if (d > dist[u]) continue;
            for (const [v, w] of g[u]) {
                if (dist[v] > d + w) {
                    dist[v] = d + w;
                    h.push([dist[v], v]);
                }
            }
        }
        const order = Array.from({length: n}, (_, i) => i+1).sort((a, b) => dist[a] - dist[b]);
        const dp = Array(n+1).fill(0);
        dp[n] = 1;
        for (const u of order) {
            for (const [v, _] of g[u]) {
                if (dist[u] > dist[v]) {
                    dp[u] = (dp[u] + dp[v]) % MOD;
                }
            }
        }
        return dp[1];
    }
}

Complexity

⏰ Time complexity: O((n + m) log n), where n is the number of nodes and m is the number of edges; Dijkstra’s algorithm dominates.
🧺 Space complexity: O(n + m), for the graph, distance, and DP arrays.

Number of Restricted Paths From First to Last Node Problem#

Problem#

Examples#

Solution#

Method 1 – Dijkstra + DP#

Intuition#

Approach#

Code#

Complexity#