problemmediumalgorithmsleetcode-1621leetcode 1621leetcode1621

Number of Sets of K Non-Overlapping Line Segments

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

Given n points on a 1-D plane, where the ith point (from 0 to n-1) is at x = i, find the number of ways we can draw exactly k non-overlapping line segments such that each segment covers two or more points. The endpoints of each segment must have integral coordinates. The k line segments do not have to cover all n points, and they are allowed to share endpoints.

Return the number of ways we can draw k non-overlapping line segments_._ Since this number can be huge, return it modulo 10^9 + 7.

Examples

Example 1

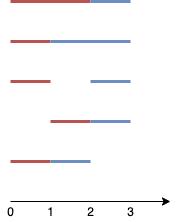
Input: n = 4, k = 2
Output: 5
Explanation: The two line segments are shown in red and blue.
The image above shows the 5 different ways {(0,2),(2,3)}, {(0,1),(1,3)}, {(0,1),(2,3)}, {(1,2),(2,3)}, {(0,1),(1,2)}.

Example 2

Input: n = 3, k = 1
Output: 3
Explanation: The 3 ways are {(0,1)}, {(0,2)}, {(1,2)}.

Example 3

Input: n = 30, k = 7
Output: 796297179
Explanation: The total number of possible ways to draw 7 line segments is 3796297200. Taking this number modulo 109 + 7 gives us 796297179.

Solution

Method 1 – Dynamic Programming with Combinatorics

Intuition

We need to count the number of ways to draw k non-overlapping segments on n points, where each segment covers at least two points. This is a classic combinatorial DP problem, where we can use DP to count the ways by considering whether to start a segment at each point or not.

Approach

  1. Use a DP table dp[i][j] where i is the number of points considered and j is the number of segments drawn.
  2. For each point, either:
    • Do not start a segment at this point (carry over previous value).
    • Start a segment ending at this point (consider all possible starts for the segment).
  3. Use prefix sums or combinatorial identities to optimize transitions.
  4. The answer is dp[n][k] modulo 10^9+7.

Code

C++
const int MOD = 1e9+7;
class Solution {
public:
    int numberOfSets(int n, int k) {
        vector<vector<int>> dp(n+1, vector<int>(k+1, 0));
        for (int i = 0; i <= n; ++i) dp[i][0] = 1;
        for (int seg = 1; seg <= k; ++seg) {
            for (int i = seg*2; i <= n; ++i) {
                for (int j = seg*2-1; j < i; ++j) {
                    dp[i][seg] = (dp[i][seg] + dp[j][seg-1]) % MOD;
                }
            }
        }
        return dp[n][k];
    }
};
Go
const MOD = 1e9+7
func numberOfSets(n, k int) int {
    dp := make([][]int, n+1)
    for i := range dp {
        dp[i] = make([]int, k+1)
        dp[i][0] = 1
    }
    for seg := 1; seg <= k; seg++ {
        for i := seg*2; i <= n; i++ {
            for j := seg*2-1; j < i; j++ {
                dp[i][seg] = (dp[i][seg] + dp[j][seg-1]) % MOD
            }
        }
    }
    return dp[n][k]
}
Java
class Solution {
    static final int MOD = 1000000007;
    public int numberOfSets(int n, int k) {
        int[][] dp = new int[n+1][k+1];
        for (int i = 0; i <= n; i++) dp[i][0] = 1;
        for (int seg = 1; seg <= k; seg++) {
            for (int i = seg*2; i <= n; i++) {
                for (int j = seg*2-1; j < i; j++) {
                    dp[i][seg] = (dp[i][seg] + dp[j][seg-1]) % MOD;
                }
            }
        }
        return dp[n][k];
    }
}
Kotlin
class Solution {
    private val MOD = 1000000007
    fun numberOfSets(n: Int, k: Int): Int {
        val dp = Array(n+1) { IntArray(k+1) }
        for (i in 0..n) dp[i][0] = 1
        for (seg in 1..k) {
            for (i in seg*2..n) {
                for (j in seg*2-1 until i) {
                    dp[i][seg] = (dp[i][seg] + dp[j][seg-1]) % MOD
                }
            }
        }
        return dp[n][k]
    }
}
Python
def numberOfSets(n: int, k: int) -> int:
    MOD = 10**9+7
    dp = [[0]*(k+1) for _ in range(n+1)]
    for i in range(n+1):
        dp[i][0] = 1
    for seg in range(1, k+1):
        for i in range(seg*2, n+1):
            for j in range(seg*2-1, i):
                dp[i][seg] = (dp[i][seg] + dp[j][seg-1]) % MOD
    return dp[n][k]
Rust
const MOD: i32 = 1_000_000_007;
impl Solution {
    pub fn number_of_sets(n: i32, k: i32) -> i32 {
        let n = n as usize;
        let k = k as usize;
        let mut dp = vec![vec![0; k+1]; n+1];
        for i in 0..=n { dp[i][0] = 1; }
        for seg in 1..=k {
            for i in seg*2..=n {
                for j in seg*2-1..i {
                    dp[i][seg] = (dp[i][seg] + dp[j][seg-1]) % MOD;
                }
            }
        }
        dp[n][k]
    }
}
TypeScript
const MOD = 1e9+7;
class Solution {
    numberOfSets(n: number, k: number): number {
        const dp: number[][] = Array.from({length: n+1}, () => Array(k+1).fill(0));
        for (let i = 0; i <= n; i++) dp[i][0] = 1;
        for (let seg = 1; seg <= k; seg++) {
            for (let i = seg*2; i <= n; i++) {
                for (let j = seg*2-1; j < i; j++) {
                    dp[i][seg] = (dp[i][seg] + dp[j][seg-1]) % MOD;
                }
            }
        }
        return dp[n][k];
    }
}

Complexity

  • ⏰ Time complexity: O(n^2*k), since for each segment and point, we may iterate over previous points.
  • 🧺 Space complexity: O(n*k), for the DP table.

Comments