Problem

There is an 8 x 8 chessboard containing n pieces (rooks, queens, or bishops). You are given a string array pieces of length n, where pieces[i] describes the type (rook, queen, or bishop) of the ith piece. In addition, you are given a 2D integer array positions also of length n, where positions[i] = [ri, ci] indicates that the ith piece is currently at the 1-based coordinate (ri, ci) on the chessboard.

When making a move for a piece, you choose a destination square that the piece will travel toward and stop on.

  • A rook can only travel horizontally or vertically from (r, c) to the direction of (r+1, c), (r-1, c), (r, c+1), or (r, c-1).
  • A queen can only travel horizontally, vertically, or diagonally from (r, c) to the direction of (r+1, c), (r-1, c), (r, c+1), (r, c-1), (r+1, c+1), (r+1, c-1), (r-1, c+1), (r-1, c-1).
  • A bishop can only travel diagonally from (r, c) to the direction of (r+1, c+1), (r+1, c-1), (r-1, c+1), (r-1, c-1).

You must make a move for every piece on the board simultaneously. A move combination consists of all the moves performed on all the given pieces. Every second, each piece will instantaneously travel one square towards their destination if they are not already at it. All pieces start traveling at the 0th second. A move combination is invalid if, at a given time, two or more pieces occupy the same square.

Return _the number ofvalid move combinations_​​​​​.

Notes:

  • No two pieces will start in thesame square.
  • You may choose the square a piece is already on as its destination.
  • If two pieces are directly adjacent to each other, it is valid for them to move past each other and swap positions in one second.

Examples

Example 1

1
2
3
4
5
6


![](https://assets.leetcode.com/uploads/2021/09/23/a1.png)

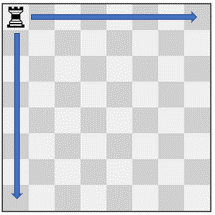
Input: pieces = ["rook"], positions = [[1,1]]
Output: 15
Explanation: The image above shows the possible squares the piece can move to.

Example 2

1
2
3
4
5
6


![](https://assets.leetcode.com/uploads/2021/09/23/a2.png)

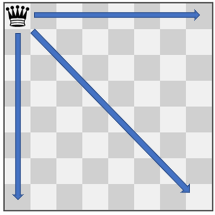
Input: pieces = ["queen"], positions = [[1,1]]
Output: 22
Explanation: The image above shows the possible squares the piece can move to.

Example 3

1
2
3
4
5
6


![](https://assets.leetcode.com/uploads/2021/09/23/a3.png)

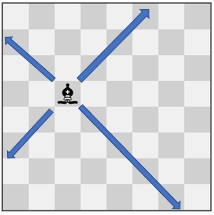
Input: pieces = ["bishop"], positions = [[4,3]]
Output: 12
Explanation: The image above shows the possible squares the piece can move to.

Constraints

  • n == pieces.length
  • n == positions.length
  • 1 <= n <= 4
  • pieces only contains the strings "rook", "queen", and "bishop".
  • There will be at most one queen on the chessboard.
  • 1 <= ri, ci <= 8
  • Each positions[i] is distinct.

Solution

Method 1 – Backtracking with Simulation

Intuition

Since n ≤ 4, we can try all possible destinations for each piece. For each combination, simulate the movement step by step and check for collisions. If no collision occurs, the combination is valid.

Approach

  1. For each piece, generate all possible destinations it can reach (including its current position).
  2. For each combination of destinations (cartesian product), simulate the movement of all pieces step by step.
  3. At each time step, move each piece one square toward its destination. If two pieces occupy the same square at the same time, the combination is invalid.
  4. If all pieces reach their destinations without collision, count the combination as valid.
  5. Return the total number of valid combinations.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

class Solution {
public:
    int countCombinations(vector<string>& pieces, vector<vector<int>>& positions) {
        vector<vector<pair<int,int>>> moves = {
            {{1,0},{-1,0},{0,1},{0,-1}}, // rook
            {{1,0},{-1,0},{0,1},{0,-1},{1,1},{1,-1},{-1,1},{-1,-1}}, // queen
            {{1,1},{1,-1},{-1,1},{-1,-1}} // bishop
        };
        int n = pieces.size(), ans = 0;
        vector<vector<pair<int,int>>> dests(n);
        for (int i = 0; i < n; ++i) {
            set<pair<int,int>> s;
            int t = pieces[i] == "rook" ? 0 : pieces[i] == "queen" ? 1 : 2;
            int r = positions[i][0], c = positions[i][1];
            s.insert({r,c});
            for (auto [dr,dc] : moves[t]) {
                for (int k = 1; k < 8; ++k) {
                    int nr = r + dr*k, nc = c + dc*k;
                    if (nr < 1 || nr > 8 || nc < 1 || nc > 8) break;
                    s.insert({nr,nc});
                }
            }
            dests[i] = vector<pair<int,int>>(s.begin(), s.end());
        }
        vector<int> idx(n);
        function<void(int)> dfs = [&](int d) {
            if (d == n) {
                vector<pair<int,int>> cur = positions;
                set<vector<pair<int,int>>> seen;
                bool ok = true;
                while (true) {
                    vector<pair<int,int>> nxt = cur;
                    bool done = true;
                    for (int i = 0; i < n; ++i) {
                        if (cur[i] != dests[i][idx[i]]) {
                            int dr = dests[i][idx[i]].first - cur[i].first;
                            int dc = dests[i][idx[i]].second - cur[i].second;
                            nxt[i].first += (dr == 0 ? 0 : dr/abs(dr));
                            nxt[i].second += (dc == 0 ? 0 : dc/abs(dc));
                            done = false;
                        }
                    }
                    set<pair<int,int>> s(nxt.begin(), nxt.end());
                    if (s.size() < n) { ok = false; break; }
                    if (done) break;
                    cur = nxt;
                }
                if (ok) ans++;
                return;
            }
            for (int i = 0; i < dests[d].size(); ++i) {
                idx[d] = i;
                dfs(d+1);
            }
        };
        dfs(0);
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

func countCombinations(pieces []string, positions [][]int) int {
    moves := [][][2]int{
        {{1,0},{-1,0},{0,1},{0,-1}},
        {{1,0},{-1,0},{0,1},{0,-1},{1,1},{1,-1},{-1,1},{-1,-1}},
        {{1,1},{1,-1},{-1,1},{-1,-1}},
    }
    n, ans := len(pieces), 0
    dests := make([][][2]int, n)
    for i := 0; i < n; i++ {
        s := map[[2]int]struct{}{}
        t := 0
        if pieces[i] == "queen" { t = 1 } else if pieces[i] == "bishop" { t = 2 }
        r, c := positions[i][0], positions[i][1]
        s[[2]int{r,c}] = struct{}{}
        for _, d := range moves[t] {
            for k := 1; k < 8; k++ {
                nr, nc := r+d[0]*k, c+d[1]*k
                if nr < 1 || nr > 8 || nc < 1 || nc > 8 { break }
                s[[2]int{nr,nc}] = struct{}{}
            }
        }
        for p := range s { dests[i] = append(dests[i], p) }
    }
    idx := make([]int, n)
    var dfs func(int)
    dfs = func(d int) {
        if d == n {
            cur := make([][2]int, n)
            for i := range positions { cur[i] = [2]int{positions[i][0], positions[i][1]} }
            ok := true
            for {
                nxt := make([][2]int, n)
                copy(nxt, cur)
                done := true
                for i := 0; i < n; i++ {
                    if cur[i] != dests[i][idx[i]] {
                        dr := dests[i][idx[i]][0] - cur[i][0]
                        dc := dests[i][idx[i]][1] - cur[i][1]
                        if dr != 0 { nxt[i][0] += dr/abs(dr) }
                        if dc != 0 { nxt[i][1] += dc/abs(dc) }
                        done = false
                    }
                }
                s := map[[2]int]struct{}{}
                for _, p := range nxt { s[p] = struct{}{} }
                if len(s) < n { ok = false; break }
                if done { break }
                copy(cur, nxt)
            }
            if ok { ans++ }
            return
        }
        for i := 0; i < len(dests[d]); i++ {
            idx[d] = i
            dfs(d+1)
        }
    }
    dfs(0)
    return ans
}
func abs(x int) int { if x < 0 { return -x }; return x }
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

class Solution {
    public int countCombinations(String[] pieces, int[][] positions) {
        int[][][] moves = {
            {{1,0},{-1,0},{0,1},{0,-1}},
            {{1,0},{-1,0},{0,1},{0,-1},{1,1},{1,-1},{-1,1},{-1,-1}},
            {{1,1},{1,-1},{-1,1},{-1,-1}}
        };
        int n = pieces.length, ans = 0;
        List<List<int[]>> dests = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            Set<String> s = new HashSet<>();
            int t = pieces[i].equals("rook") ? 0 : pieces[i].equals("queen") ? 1 : 2;
            int r = positions[i][0], c = positions[i][1];
            s.add(r+","+c);
            for (int[] d : moves[t]) {
                for (int k = 1; k < 8; k++) {
                    int nr = r + d[0]*k, nc = c + d[1]*k;
                    if (nr < 1 || nr > 8 || nc < 1 || nc > 8) break;
                    s.add(nr+","+nc);
                }
            }
            List<int[]> list = new ArrayList<>();
            for (String key : s) {
                String[] parts = key.split(",");
                list.add(new int[]{Integer.parseInt(parts[0]), Integer.parseInt(parts[1])});
            }
            dests.add(list);
        }
        int[] idx = new int[n];
        ans = dfs(0, n, dests, idx, positions);
        return ans;
    }
    private int dfs(int d, int n, List<List<int[]>> dests, int[] idx, int[][] positions) {
        if (d == n) {
            int[][] cur = new int[n][2];
            for (int i = 0; i < n; i++) cur[i] = positions[i].clone();
            boolean ok = true;
            while (true) {
                int[][] nxt = new int[n][2];
                for (int i = 0; i < n; i++) nxt[i] = cur[i].clone();
                boolean done = true;
                for (int i = 0; i < n; i++) {
                    if (cur[i][0] != dests.get(i).get(idx[i])[0] || cur[i][1] != dests.get(i).get(idx[i])[1]) {
                        int dr = dests.get(i).get(idx[i])[0] - cur[i][0];
                        int dc = dests.get(i).get(idx[i])[1] - cur[i][1];
                        if (dr != 0) nxt[i][0] += dr/Math.abs(dr);
                        if (dc != 0) nxt[i][1] += dc/Math.abs(dc);
                        done = false;
                    }
                }
                Set<String> s = new HashSet<>();
                for (int[] p : nxt) s.add(p[0]+","+p[1]);
                if (s.size() < n) { ok = false; break; }
                if (done) break;
                for (int i = 0; i < n; i++) cur[i] = nxt[i];
            }
            return ok ? 1 : 0;
        }
        int res = 0;
        for (int i = 0; i < dests.get(d).size(); i++) {
            idx[d] = i;
            res += dfs(d+1, n, dests, idx, positions);
        }
        return res;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

class Solution {
    fun countCombinations(pieces: Array<String>, positions: Array<IntArray>): Int {
        val moves = arrayOf(
            arrayOf(intArrayOf(1,0), intArrayOf(-1,0), intArrayOf(0,1), intArrayOf(0,-1)),
            arrayOf(intArrayOf(1,0), intArrayOf(-1,0), intArrayOf(0,1), intArrayOf(0,-1), intArrayOf(1,1), intArrayOf(1,-1), intArrayOf(-1,1), intArrayOf(-1,-1)),
            arrayOf(intArrayOf(1,1), intArrayOf(1,-1), intArrayOf(-1,1), intArrayOf(-1,-1))
        )
        val n = pieces.size
        val dests = Array(n) { mutableSetOf<Pair<Int,Int>>() }
        for (i in 0 until n) {
            val t = when (pieces[i]) { "rook" -> 0; "queen" -> 1; else -> 2 }
            val (r, c) = positions[i]
            dests[i].add(r to c)
            for (d in moves[t]) {
                for (k in 1..7) {
                    val nr = r + d[0]*k; val nc = c + d[1]*k
                    if (nr !in 1..8 || nc !in 1..8) break
                    dests[i].add(nr to nc)
                }
            }
        }
        val destList = dests.map { it.toList() }
        val idx = IntArray(n)
        fun dfs(d: Int): Int {
            if (d == n) {
                var cur = positions.map { it.copyOf() }.toTypedArray()
                var ok = true
                while (true) {
                    val nxt = cur.map { it.copyOf() }.toTypedArray()
                    var done = true
                    for (i in 0 until n) {
                        if (cur[i][0] != destList[i][idx[i]].first || cur[i][1] != destList[i][idx[i]].second) {
                            val dr = destList[i][idx[i]].first - cur[i][0]
                            val dc = destList[i][idx[i]].second - cur[i][1]
                            if (dr != 0) nxt[i][0] += dr/Math.abs(dr)
                            if (dc != 0) nxt[i][1] += dc/Math.abs(dc)
                            done = false
                        }
                    }
                    val s = nxt.map { it[0] to it[1] }.toSet()
                    if (s.size < n) { ok = false; break }
                    if (done) break
                    cur = nxt
                }
                return if (ok) 1 else 0
            }
            var res = 0
            for (i in destList[d].indices) {
                idx[d] = i
                res += dfs(d+1)
            }
            return res
        }
        return dfs(0)
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

class Solution:
    def countCombinations(self, pieces: list[str], positions: list[list[int]]) -> int:
        moves = {
            'rook': [(1,0),(-1,0),(0,1),(0,-1)],
            'queen': [(1,0),(-1,0),(0,1),(0,-1),(1,1),(1,-1),(-1,1),(-1,-1)],
            'bishop': [(1,1),(1,-1),(-1,1),(-1,-1)]
        }
        n = len(pieces)
        dests = []
        for i in range(n):
            s = set()
            r, c = positions[i]
            s.add((r,c))
            for dr, dc in moves[pieces[i]]:
                for k in range(1,8):
                    nr, nc = r+dr*k, c+dc*k
                    if not (1 <= nr <= 8 and 1 <= nc <= 8): break
                    s.add((nr,nc))
            dests.append(list(s))
        ans = 0
        idx = [0]*n
        def dfs(d):
            nonlocal ans
            if d == n:
                cur = [list(p) for p in positions]
                ok = True
                while True:
                    nxt = [c[:] for c in cur]
                    done = True
                    for i in range(n):
                        if cur[i] != list(dests[i][idx[i]]):
                            dr = dests[i][idx[i]][0] - cur[i][0]
                            dc = dests[i][idx[i]][1] - cur[i][1]
                            if dr != 0: nxt[i][0] += dr//abs(dr)
                            if dc != 0: nxt[i][1] += dc//abs(dc)
                            done = False
                    if len({tuple(x) for x in nxt}) < n:
                        ok = False; break
                    if done: break
                    cur = nxt
                if ok: ans += 1
                return
            for i in range(len(dests[d])):
                idx[d] = i
                dfs(d+1)
        dfs(0)
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

impl Solution {
    pub fn count_combinations(pieces: Vec<String>, positions: Vec<Vec<i32>>) -> i32 {
        let moves = [
            vec![(1,0),(-1,0),(0,1),(0,-1)],
            vec![(1,0),(-1,0),(0,1),(0,-1),(1,1),(1,-1),(-1,1),(-1,-1)],
            vec![(1,1),(1,-1),(-1,1),(-1,-1)]
        ];
        let n = pieces.len();
        let mut dests = vec![vec![]; n];
        for i in 0..n {
            let mut s = std::collections::HashSet::new();
            let (r, c) = (positions[i][0], positions[i][1]);
            s.insert((r, c));
            let t = if pieces[i] == "rook" { 0 } else if pieces[i] == "queen" { 1 } else { 2 };
            for &(dr, dc) in &moves[t] {
                for k in 1..8 {
                    let nr = r + dr*k;
                    let nc = c + dc*k;
                    if nr < 1 || nr > 8 || nc < 1 || nc > 8 { break; }
                    s.insert((nr, nc));
                }
            }
            dests[i] = s.into_iter().collect();
        }
        let mut ans = 0;
        let mut idx = vec![0; n];
        fn dfs(d: usize, n: usize, dests: &Vec<Vec<(i32,i32)>>, idx: &mut Vec<usize>, positions: &Vec<Vec<i32>>, ans: &mut i32) {
            if d == n {
                let mut cur: Vec<(i32,i32)> = positions.iter().map(|p| (p[0],p[1])).collect();
                let mut ok = true;
                loop {
                    let mut nxt = cur.clone();
                    let mut done = true;
                    for i in 0..n {
                        if cur[i] != dests[i][idx[i]] {
                            let dr = dests[i][idx[i]].0 - cur[i].0;
                            let dc = dests[i][idx[i]].1 - cur[i].1;
                            if dr != 0 { nxt[i].0 += dr/dr.abs(); }
                            if dc != 0 { nxt[i].1 += dc/dc.abs(); }
                            done = false;
                        }
                    }
                    let s: std::collections::HashSet<_> = nxt.iter().collect();
                    if s.len() < n { ok = false; break; }
                    if done { break; }
                    cur = nxt;
                }
                if ok { *ans += 1; }
                return;
            }
            for i in 0..dests[d].len() {
                idx[d] = i;
                dfs(d+1, n, dests, idx, positions, ans);
            }
        }
        dfs(0, n, &dests, &mut idx, &positions, &mut ans);
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

class Solution {
    countCombinations(pieces: string[], positions: number[][]): number {
        const moves = [
            [[1,0],[-1,0],[0,1],[0,-1]],
            [[1,0],[-1,0],[0,1],[0,-1],[1,1],[1,-1],[-1,1],[-1,-1]],
            [[1,1],[1,-1],[-1,1],[-1,-1]]
        ]
        const n = pieces.length
        const dests: Set<string>[] = Array.from({length: n}, () => new Set())
        for (let i = 0; i < n; i++) {
            const t = pieces[i] === 'rook' ? 0 : pieces[i] === 'queen' ? 1 : 2
            const [r, c] = positions[i]
            dests[i].add(`${r},${c}`)
            for (const [dr, dc] of moves[t]) {
                for (let k = 1; k < 8; k++) {
                    const nr = r + dr*k, nc = c + dc*k
                    if (nr < 1 || nr > 8 || nc < 1 || nc > 8) break
                    dests[i].add(`${nr},${nc}`)
                }
            }
        }
        const destArr = dests.map(s => Array.from(s))
        const idx = new Array(n).fill(0)
        let ans = 0
        function dfs(d: number) {
            if (d === n) {
                let cur = positions.map(p => [...p])
                let ok = true
                while (true) {
                    const nxt = cur.map(p => [...p])
                    let done = true
                    for (let i = 0; i < n; i++) {
                        const [tr, tc] = destArr[i][idx[i]].split(',').map(Number)
                        if (cur[i][0] !== tr || cur[i][1] !== tc) {
                            const dr = tr - cur[i][0], dc = tc - cur[i][1]
                            if (dr !== 0) nxt[i][0] += dr/Math.abs(dr)
                            if (dc !== 0) nxt[i][1] += dc/Math.abs(dc)
                            done = false
                        }
                    }
                    const s = new Set(nxt.map(p => p.join(',')))
                    if (s.size < n) { ok = false; break }
                    if (done) break
                    cur = nxt
                }
                if (ok) ans++
                return
            }
            for (let i = 0; i < destArr[d].length; i++) {
                idx[d] = i
                dfs(d+1)
            }
        }
        dfs(0)
        return ans
    }
}

Complexity

  • ⏰ Time complexity: O((M^n) * T), where M is the max number of destinations per piece, n is the number of pieces (≤4), and T is the max number of steps to simulate.
  • 🧺 Space complexity: O(M^n), for recursion and destination storage.