Problem

Given a rectangular pizza represented as a rows x cols matrix containing the following characters: 'A' (an apple) and '.' (empty cell) and given the integer k. You have to cut the pizza into k pieces using k-1 cuts. 

For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.

Return the number of ways of cutting the pizza such that each piece contains at least one apple. Since the answer can be a huge number, return this modulo 10^9 + 7.

Examples

Example 1:

1
2
3
4
5

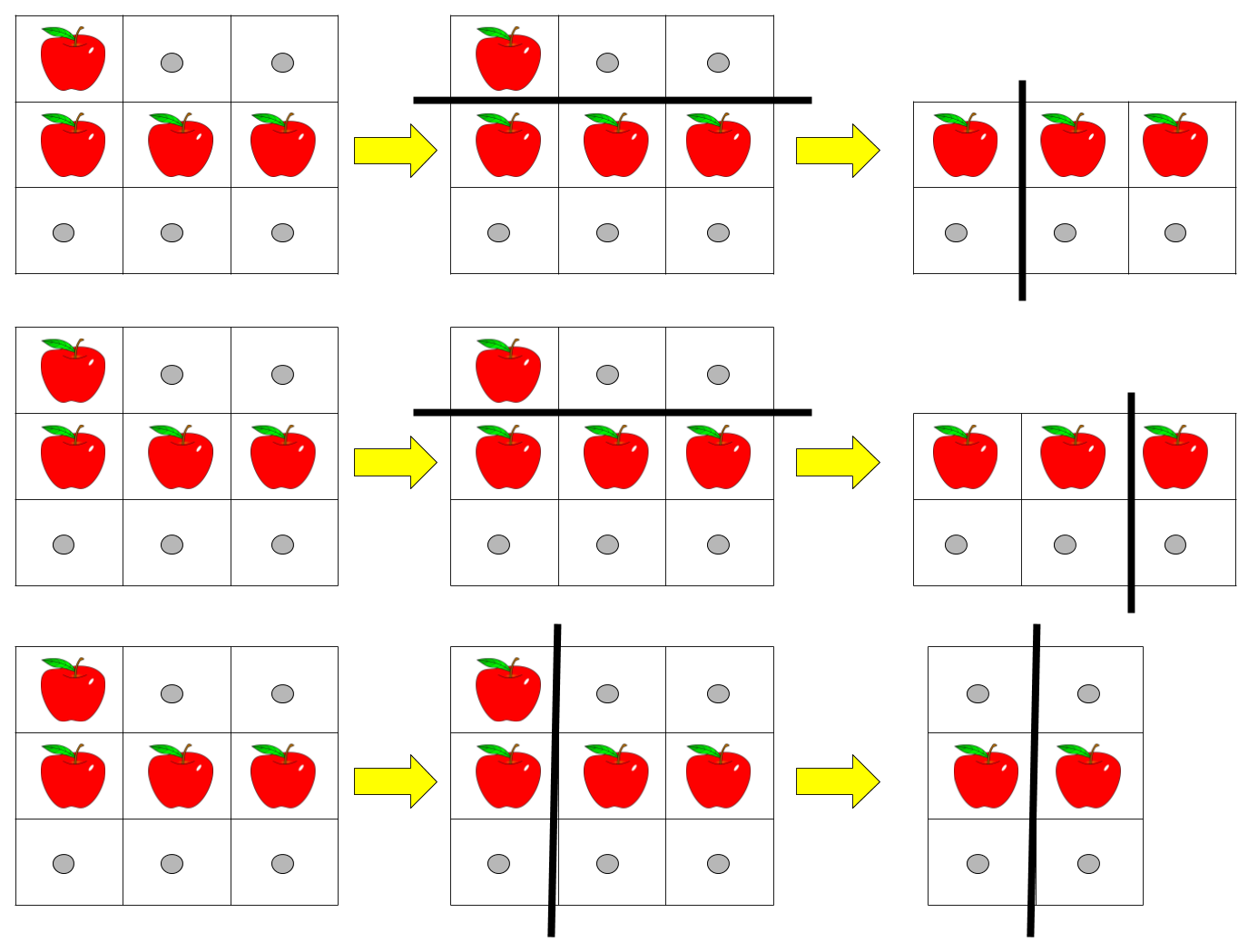
Input:
pizza = ["A..","AAA","..."], k = 3
Output:
 3 
Explanation: The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.

Example 2:

1
2
3
4

Input:
pizza = ["A..","AA.","..."], k = 3
Output:
 1

Example 3:

1
2
3
4

Input:
pizza = ["A..","A..","..."], k = 1
Output:
 1

Solution

Method 1 – Dynamic Programming with Memoization

Intuition

We use dynamic programming to count the number of ways to cut the pizza, ensuring each piece contains at least one apple. By precomputing the number of apples in each submatrix, we can quickly check if a cut is valid.

Approach

  1. Precompute a prefix sum matrix to count apples in any submatrix.
  2. Use a recursive DP function dp(r, c, k) to count ways to cut the pizza starting at (r, c) with k pieces left.
  3. For each possible horizontal and vertical cut, check if the piece to be given away contains at least one apple using the prefix sum.
  4. Memoize results to avoid recomputation.
  5. Return the total number of ways modulo 10^9 + 7.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
public:
    int ways(vector<string>& pizza, int k) {
        int MOD = 1e9 + 7, rows = pizza.size(), cols = pizza[0].size();
        vector<vector<int>> apples(rows + 1, vector<int>(cols + 1));
        for (int r = rows - 1; r >= 0; --r)
            for (int c = cols - 1; c >= 0; --c)
                apples[r][c] = (pizza[r][c] == 'A') + apples[r + 1][c] + apples[r][c + 1] - apples[r + 1][c + 1];
        vector<vector<vector<int>>> dp(rows, vector<vector<int>>(cols, vector<int>(k, -1)));
        function<int(int,int,int)> dfs = [&](int r, int c, int cuts) {
            if (apples[r][c] == 0) return 0;
            if (cuts == 0) return 1;
            if (dp[r][c][cuts] != -1) return dp[r][c][cuts];
            int ans = 0;
            for (int nr = r + 1; nr < rows; ++nr)
                if (apples[r][c] - apples[nr][c] > 0)
                    ans = (ans + dfs(nr, c, cuts - 1)) % MOD;
            for (int nc = c + 1; nc < cols; ++nc)
                if (apples[r][c] - apples[r][nc] > 0)
                    ans = (ans + dfs(r, nc, cuts - 1)) % MOD;
            return dp[r][c][cuts] = ans;
        };
        return dfs(0, 0, k - 1);
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

func ways(pizza []string, k int) int {
    MOD := int(1e9 + 7)
    rows, cols := len(pizza), len(pizza[0])
    apples := make([][]int, rows+1)
    for i := range apples {
        apples[i] = make([]int, cols+1)
    }
    for r := rows - 1; r >= 0; r-- {
        for c := cols - 1; c >= 0; c-- {
            apples[r][c] = boolToInt(pizza[r][c] == 'A') + apples[r+1][c] + apples[r][c+1] - apples[r+1][c+1]
        }
    }
    dp := make([][][]int, rows)
    for i := range dp {
        dp[i] = make([][]int, cols)
        for j := range dp[i] {
            dp[i][j] = make([]int, k)
            for l := range dp[i][j] {
                dp[i][j][l] = -1
            }
        }
    }
    var dfs func(int, int, int) int
    dfs = func(r, c, cuts int) int {
        if apples[r][c] == 0 {
            return 0
        }
        if cuts == 0 {
            return 1
        }
        if dp[r][c][cuts] != -1 {
            return dp[r][c][cuts]
        }
        ans := 0
        for nr := r + 1; nr < rows; nr++ {
            if apples[r][c]-apples[nr][c] > 0 {
                ans = (ans + dfs(nr, c, cuts-1)) % MOD
            }
        }
        for nc := c + 1; nc < cols; nc++ {
            if apples[r][c]-apples[r][nc] > 0 {
                ans = (ans + dfs(r, nc, cuts-1)) % MOD
            }
        }
        dp[r][c][cuts] = ans
        return ans
    }
    return dfs(0, 0, k-1)
}

func boolToInt(b bool) int {
    if b {
        return 1
    }
    return 0
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
    public int ways(String[] pizza, int k) {
        int MOD = 1000000007, rows = pizza.length, cols = pizza[0].length();
        int[][] apples = new int[rows + 1][cols + 1];
        for (int r = rows - 1; r >= 0; --r)
            for (int c = cols - 1; c >= 0; --c)
                apples[r][c] = (pizza[r].charAt(c) == 'A' ? 1 : 0) + apples[r + 1][c] + apples[r][c + 1] - apples[r + 1][c + 1];
        int[][][] dp = new int[rows][cols][k];
        for (int[][] arr2d : dp)
            for (int[] arr1d : arr2d)
                Arrays.fill(arr1d, -1);
        return dfs(0, 0, k - 1, apples, dp, rows, cols, MOD);
    }
    private int dfs(int r, int c, int cuts, int[][] apples, int[][][] dp, int rows, int cols, int MOD) {
        if (apples[r][c] == 0) return 0;
        if (cuts == 0) return 1;
        if (dp[r][c][cuts] != -1) return dp[r][c][cuts];
        int ans = 0;
        for (int nr = r + 1; nr < rows; ++nr)
            if (apples[r][c] - apples[nr][c] > 0)
                ans = (ans + dfs(nr, c, cuts - 1, apples, dp, rows, cols, MOD)) % MOD;
        for (int nc = c + 1; nc < cols; ++nc)
            if (apples[r][c] - apples[r][nc] > 0)
                ans = (ans + dfs(r, nc, cuts - 1, apples, dp, rows, cols, MOD)) % MOD;
        return dp[r][c][cuts] = ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
    fun ways(pizza: Array<String>, k: Int): Int {
        val MOD = 1_000_000_007
        val rows = pizza.size
        val cols = pizza[0].length
        val apples = Array(rows + 1) { IntArray(cols + 1) }
        for (r in rows - 1 downTo 0)
            for (c in cols - 1 downTo 0)
                apples[r][c] = if (pizza[r][c] == 'A') 1 else 0 + apples[r + 1][c] + apples[r][c + 1] - apples[r + 1][c + 1]
        val dp = Array(rows) { Array(cols) { IntArray(k) { -1 } } }
        fun dfs(r: Int, c: Int, cuts: Int): Int {
            if (apples[r][c] == 0) return 0
            if (cuts == 0) return 1
            if (dp[r][c][cuts] != -1) return dp[r][c][cuts]
            var ans = 0
            for (nr in r + 1 until rows)
                if (apples[r][c] - apples[nr][c] > 0)
                    ans = (ans + dfs(nr, c, cuts - 1)) % MOD
            for (nc in c + 1 until cols)
                if (apples[r][c] - apples[r][nc] > 0)
                    ans = (ans + dfs(r, nc, cuts - 1)) % MOD
            dp[r][c][cuts] = ans
            return ans
        }
        return dfs(0, 0, k - 1)
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution:
    def ways(self, pizza: list[str], k: int) -> int:
        MOD = 10**9 + 7
        rows, cols = len(pizza), len(pizza[0])
        apples = [[0] * (cols + 1) for _ in range(rows + 1)]
        for r in range(rows - 1, -1, -1):
            for c in range(cols - 1, -1, -1):
                apples[r][c] = (pizza[r][c] == 'A') + apples[r + 1][c] + apples[r][c + 1] - apples[r + 1][c + 1]
        from functools import lru_cache
        @lru_cache(None)
        def dfs(r: int, c: int, cuts: int) -> int:
            if apples[r][c] == 0:
                return 0
            if cuts == 0:
                return 1
            ans = 0
            for nr in range(r + 1, rows):
                if apples[r][c] - apples[nr][c] > 0:
                    ans = (ans + dfs(nr, c, cuts - 1)) % MOD
            for nc in range(c + 1, cols):
                if apples[r][c] - apples[r][nc] > 0:
                    ans = (ans + dfs(r, nc, cuts - 1)) % MOD
            return ans
        return dfs(0, 0, k - 1)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

impl Solution {
    pub fn ways(pizza: Vec<String>, k: i32) -> i32 {
        let mod_val = 1_000_000_007;
        let rows = pizza.len();
        let cols = pizza[0].len();
        let mut apples = vec![vec![0; cols + 1]; rows + 1];
        for r in (0..rows).rev() {
            for c in (0..cols).rev() {
                apples[r][c] = (pizza[r].as_bytes()[c] == b'A') as i32 + apples[r + 1][c] + apples[r][c + 1] - apples[r + 1][c + 1];
            }
        }
        let mut dp = vec![vec![vec![-1; k as usize]; cols]; rows];
        fn dfs(r: usize, c: usize, cuts: usize, apples: &Vec<Vec<i32>>, dp: &mut Vec<Vec<Vec<i32>>>, rows: usize, cols: usize, k: usize, mod_val: i32) -> i32 {
            if apples[r][c] == 0 { return 0; }
            if cuts == 0 { return 1; }
            if dp[r][c][cuts] != -1 { return dp[r][c][cuts]; }
            let mut ans = 0;
            for nr in r + 1..rows {
                if apples[r][c] - apples[nr][c] > 0 {
                    ans = (ans + dfs(nr, c, cuts - 1, apples, dp, rows, cols, k, mod_val)) % mod_val;
                }
            }
            for nc in c + 1..cols {
                if apples[r][c] - apples[r][nc] > 0 {
                    ans = (ans + dfs(r, nc, cuts - 1, apples, dp, rows, cols, k, mod_val)) % mod_val;
                }
            }
            dp[r][c][cuts] = ans;
            ans
        }
        dfs(0, 0, (k - 1) as usize, &apples, &mut dp, rows, cols, k as usize, mod_val)
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
    ways(pizza: string[], k: number): number {
        const MOD = 1e9 + 7;
        const rows = pizza.length, cols = pizza[0].length;
        const apples: number[][] = Array.from({ length: rows + 1 }, () => Array(cols + 1).fill(0));
        for (let r = rows - 1; r >= 0; --r)
            for (let c = cols - 1; c >= 0; --c)
                apples[r][c] = (pizza[r][c] === 'A' ? 1 : 0) + apples[r + 1][c] + apples[r][c + 1] - apples[r + 1][c + 1];
        const dp: number[][][] = Array.from({ length: rows }, () => Array.from({ length: cols }, () => Array(k).fill(-1)));
        const dfs = (r: number, c: number, cuts: number): number => {
            if (apples[r][c] === 0) return 0;
            if (cuts === 0) return 1;
            if (dp[r][c][cuts] !== -1) return dp[r][c][cuts];
            let ans = 0;
            for (let nr = r + 1; nr < rows; ++nr)
                if (apples[r][c] - apples[nr][c] > 0)
                    ans = (ans + dfs(nr, c, cuts - 1)) % MOD;
            for (let nc = c + 1; nc < cols; ++nc)
                if (apples[r][c] - apples[r][nc] > 0)
                    ans = (ans + dfs(r, nc, cuts - 1)) % MOD;
            return dp[r][c][cuts] = ans;
        };
        return dfs(0, 0, k - 1);
    }
}

Complexity

  • ⏰ Time complexity: O(k * rows^2 * cols^2), since for each state we try all possible horizontal and vertical cuts and memoize results.
  • 🧺 Space complexity: O(rows * cols * k), for the DP and prefix sum matrices.