Problem

You are given an integer n representing the number of playing cards you have. A house of cards meets the following conditions:

  • A house of cards consists of one or more rows of triangles and horizontal cards.
  • Triangles are created by leaning two cards against each other.
  • One card must be placed horizontally between all adjacent triangles in a row.
  • Any triangle on a row higher than the first must be placed on a horizontal card from the previous row.
  • Each triangle is placed in the leftmost available spot in the row.

Return the number ofdistinct house of cards you can build using all n cards. Two houses of cards are considered distinct if there exists a row where the two houses contain a different number of cards.

Examples

Example 1:

1
2
3
4
5

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2100-2199/2189.Number%20of%20Ways%20to%20Build%20House%20of%20Cards/images/image-20220227213243-1.png)
Input: n = 16
Output: 2
Explanation: The two valid houses of cards are shown.
The third house of cards in the diagram is not valid because the rightmost triangle on the top row is not placed on top of a horizontal card.

Example 2:

1
2
3
4

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2100-2199/2189.Number%20of%20Ways%20to%20Build%20House%20of%20Cards/images/image-20220227213306-2.png)
Input: n = 2
Output: 1
Explanation: The one valid house of cards is shown.

Example 3:

1
2
3
4
5
6
7

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2100-2199/2189.Number%20of%20Ways%20to%20Build%20House%20of%20Cards/images/image-20220227213331-3.png)
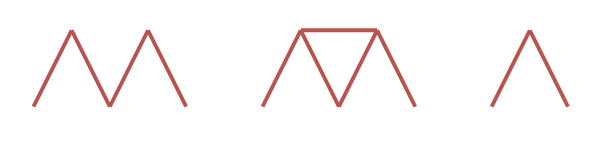
Input: n = 4
Output: 0
Explanation: The three houses of cards in the diagram are not valid.
The first house of cards needs a horizontal card placed between the two triangles.
The second house of cards uses 5 cards.
The third house of cards uses 2 cards.

Constraints:

  • 1 <= n <= 500

Solution

Method 1 – Dynamic Programming (Partition by Rows)

Intuition

Each row must have at least one triangle, and each triangle needs 2 cards, plus 1 horizontal card between every two triangles. The number of cards for a row with k triangles is 2*k + (k-1). We can use DP to count the number of ways to partition n cards into valid rows, where each row above the first must have at most as many triangles as the row below.

Approach

  1. Precompute the minimum number of cards needed for k triangles: cards = 2*k + (k-1).
  2. Use DP: dp[n][k] = number of ways to build a house with n cards and at most k triangles in the bottom row.
  3. For each possible number of triangles in the bottom row, subtract the cards used and recursively solve for the remaining cards and at most that many triangles.
  4. Base case: n == 0 is 1 way (if at least one row was used), otherwise 0.
  5. Return dp[n][max_k], where max_k is the largest possible number of triangles in the bottom row.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
public:
    int houseOfCards(int n) {
        vector<vector<int>> dp(n+1, vector<int>(n+1, -1));
        function<int(int,int)> f = [&](int rem, int maxk) {
            if (rem == 0) return 1;
            if (rem < 0 || maxk == 0) return 0;
            if (dp[rem][maxk] != -1) return dp[rem][maxk];
            int ans = 0;
            for (int k = 1; ; ++k) {
                int need = 2*k + (k-1);
                if (need > rem || k > maxk) break;
                ans += f(rem-need, k);
            }
            return dp[rem][maxk] = ans;
        };
        return f(n, n);
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

func houseOfCards(n int) int {
    dp := make([][]int, n+1)
    for i := range dp { dp[i] = make([]int, n+1); for j := range dp[i] { dp[i][j] = -1 } }
    var f func(rem, maxk int) int
    f = func(rem, maxk int) int {
        if rem == 0 { return 1 }
        if rem < 0 || maxk == 0 { return 0 }
        if dp[rem][maxk] != -1 { return dp[rem][maxk] }
        ans := 0
        for k := 1; ; k++ {
            need := 2*k + (k-1)
            if need > rem || k > maxk { break }
            ans += f(rem-need, k)
        }
        dp[rem][maxk] = ans
        return ans
    }
    return f(n, n)
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
    public int houseOfCards(int n) {
        int[][] dp = new int[n+1][n+1];
        for (int[] row : dp) Arrays.fill(row, -1);
        return f(n, n, dp);
    }
    private int f(int rem, int maxk, int[][] dp) {
        if (rem == 0) return 1;
        if (rem < 0 || maxk == 0) return 0;
        if (dp[rem][maxk] != -1) return dp[rem][maxk];
        int ans = 0;
        for (int k = 1; ; k++) {
            int need = 2*k + (k-1);
            if (need > rem || k > maxk) break;
            ans += f(rem-need, k, dp);
        }
        return dp[rem][maxk] = ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
    fun houseOfCards(n: Int): Int {
        val dp = Array(n+1) { IntArray(n+1) { -1 } }
        fun f(rem: Int, maxk: Int): Int {
            if (rem == 0) return 1
            if (rem < 0 || maxk == 0) return 0
            if (dp[rem][maxk] != -1) return dp[rem][maxk]
            var ans = 0
            for (k in 1..maxk) {
                val need = 2*k + (k-1)
                if (need > rem) break
                ans += f(rem-need, k)
            }
            dp[rem][maxk] = ans
            return ans
        }
        return f(n, n)
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution:
    def houseOfCards(self, n: int) -> int:
        from functools import lru_cache
        @lru_cache(maxsize=None)
        def f(rem: int, maxk: int) -> int:
            if rem == 0:
                return 1
            if rem < 0 or maxk == 0:
                return 0
            ans = 0
            k = 1
            while True:
                need = 2*k + (k-1)
                if need > rem or k > maxk:
                    break
                ans += f(rem-need, k)
                k += 1
            return ans
        return f(n, n)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

impl Solution {
    pub fn house_of_cards(n: i32) -> i32 {
        fn f(rem: usize, maxk: usize, dp: &mut Vec<Vec<i32>>) -> i32 {
            if rem == 0 { return 1; }
            if rem < 0 || maxk == 0 { return 0; }
            if dp[rem][maxk] != -1 { return dp[rem][maxk]; }
            let mut ans = 0;
            for k in 1..=maxk {
                let need = 2*k + (k-1);
                if need > rem { break; }
                ans += f(rem-need, k, dp);
            }
            dp[rem][maxk] = ans;
            ans
        }
        let n = n as usize;
        let mut dp = vec![vec![-1; n+1]; n+1];
        f(n, n, &mut dp)
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
    houseOfCards(n: number): number {
        const dp: number[][] = Array.from({length: n+1}, () => Array(n+1).fill(-1))
        function f(rem: number, maxk: number): number {
            if (rem === 0) return 1
            if (rem < 0 || maxk === 0) return 0
            if (dp[rem][maxk] !== -1) return dp[rem][maxk]
            let ans = 0
            for (let k = 1; k <= maxk; k++) {
                const need = 2*k + (k-1)
                if (need > rem) break
                ans += f(rem-need, k)
            }
            dp[rem][maxk] = ans
            return ans
        }
        return f(n, n)
    }
}

Complexity

  • ⏰ Time complexity: O(n^2), since we memoize for each (rem, maxk) pair.
  • 🧺 Space complexity: O(n^2), for the DP table or cache.