Number of Ways to Build Sturdy Brick Wall
Problem
You are given integers height and width which specify the dimensions of a brick wall you are building. You are also given a 0-indexed array of
unique integers bricks, where the ith brick has a height of 1 and a width of bricks[i]. You have an infinite supply of each type of brick and bricks may not be rotated.
Each row in the wall must be exactly width units long. For the wall to be
sturdy , adjacent rows in the wall should not join bricks at the same location, except at the ends of the wall.
Return the number of ways to build asturdy wall. Since the answer may be very large, return it modulo 109 + 7.
Examples
Example 1:
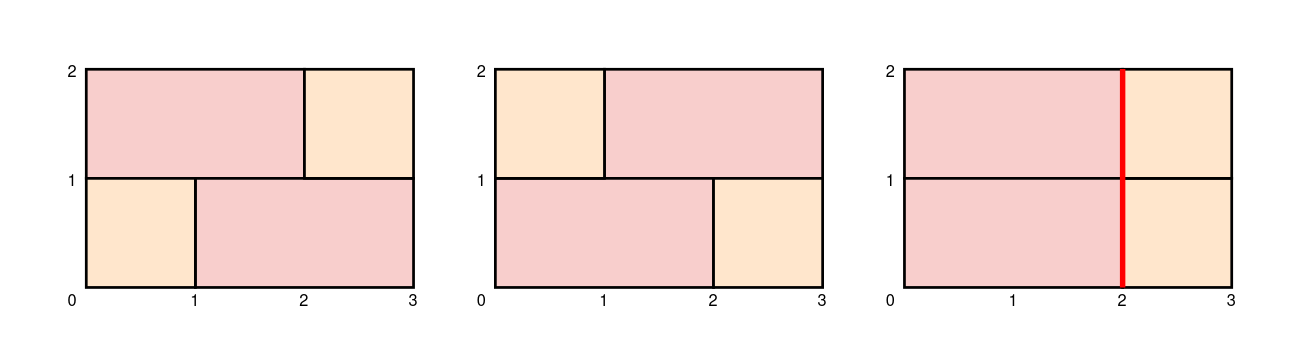
Input: height = 2, width = 3, bricks = [1,2]
Output: 2
Explanation:
The first two walls in the diagram show the only two ways to build a sturdy brick wall.
Note that the third wall in the diagram is not sturdy because adjacent rows join bricks 2 units from the left.
Example 2:
Input: height = 1, width = 1, bricks = [5]
Output: 0
Explanation:
There are no ways to build a sturdy wall because the only type of brick we have is longer than the width of the wall.
Constraints:
1 <= height <= 1001 <= width <= 101 <= bricks.length <= 101 <= bricks[i] <= 10- All the values of
bricksare unique.
Solution
Method 1 – Bitmask DP (Enumerate Row Patterns)
Intuition
Each row can be represented by the set of positions where bricks end (except the wall ends). For the wall to be sturdy, no two adjacent rows can have a brick end at the same position. Enumerate all valid row patterns, then use DP to build the wall row by row, ensuring adjacent rows are compatible.
Approach
- Generate all possible row patterns (bitmasks) for the given width and bricks.
- For each pattern, precompute which patterns are compatible (no overlapping brick ends).
- Use DP: dp[row][pattern] = number of ways to build up to this row with this pattern.
- For each row, for each pattern, sum over all compatible previous patterns.
- Return the total number of ways for the last row.
Code
C++
class Solution {
public:
int buildWall(int height, int width, vector<int>& bricks) {
const int mod = 1e9+7;
vector<int> patterns;
function<void(int,int)> dfs = [&](int pos, int mask) {
if (pos == width) { patterns.push_back(mask); return; }
for (int b : bricks) {
if (pos + b > width) continue;
int nmask = mask;
if (pos + b < width) nmask |= 1 << (pos + b);
dfs(pos + b, nmask);
}
};
dfs(0, 0);
int m = patterns.size();
vector<vector<int>> compat(m);
for (int i = 0; i < m; ++i)
for (int j = 0; j < m; ++j)
if ((patterns[i] & patterns[j]) == 0)
compat[i].push_back(j);
vector<int> dp(m, 1);
for (int h = 1; h < height; ++h) {
vector<int> ndp(m);
for (int i = 0; i < m; ++i)
for (int j : compat[i])
ndp[i] = (ndp[i] + dp[j]) % mod;
dp = ndp;
}
int ans = 0;
for (int x : dp) ans = (ans + x) % mod;
return ans;
}
};
Go
func buildWall(height, width int, bricks []int) int {
mod := int(1e9+7)
var patterns []int
var dfs func(pos, mask int)
dfs = func(pos, mask int) {
if pos == width {
patterns = append(patterns, mask)
return
}
for _, b := range bricks {
if pos+b > width { continue }
nmask := mask
if pos+b < width { nmask |= 1 << (pos+b) }
dfs(pos+b, nmask)
}
}
dfs(0, 0)
m := len(patterns)
compat := make([][]int, m)
for i := 0; i < m; i++ {
for j := 0; j < m; j++ {
if patterns[i]&patterns[j] == 0 {
compat[i] = append(compat[i], j)
}
}
}
dp := make([]int, m)
for i := range dp { dp[i] = 1 }
for h := 1; h < height; h++ {
ndp := make([]int, m)
for i := 0; i < m; i++ {
for _, j := range compat[i] {
ndp[i] = (ndp[i] + dp[j]) % mod
}
}
dp = ndp
}
ans := 0
for _, x := range dp { ans = (ans + x) % mod }
return ans
}
Java
class Solution {
public int buildWall(int height, int width, int[] bricks) {
int mod = 1_000_000_007;
List<Integer> patterns = new ArrayList<>();
dfs(0, 0, width, bricks, patterns);
int m = patterns.size();
List<Integer>[] compat = new List[m];
for (int i = 0; i < m; i++) compat[i] = new ArrayList<>();
for (int i = 0; i < m; i++)
for (int j = 0; j < m; j++)
if ((patterns.get(i) & patterns.get(j)) == 0)
compat[i].add(j);
int[] dp = new int[m];
Arrays.fill(dp, 1);
for (int h = 1; h < height; h++) {
int[] ndp = new int[m];
for (int i = 0; i < m; i++)
for (int j : compat[i])
ndp[i] = (ndp[i] + dp[j]) % mod;
dp = ndp;
}
int ans = 0;
for (int x : dp) ans = (ans + x) % mod;
return ans;
}
private void dfs(int pos, int mask, int width, int[] bricks, List<Integer> patterns) {
if (pos == width) { patterns.add(mask); return; }
for (int b : bricks) {
if (pos + b > width) continue;
int nmask = mask;
if (pos + b < width) nmask |= 1 << (pos + b);
dfs(pos + b, nmask, width, bricks, patterns);
}
}
}
Kotlin
class Solution {
fun buildWall(height: Int, width: Int, bricks: IntArray): Int {
val mod = 1_000_000_007
val patterns = mutableListOf<Int>()
fun dfs(pos: Int, mask: Int) {
if (pos == width) { patterns.add(mask); return }
for (b in bricks) {
if (pos + b > width) continue
var nmask = mask
if (pos + b < width) nmask = nmask or (1 shl (pos + b))
dfs(pos + b, nmask)
}
}
dfs(0, 0)
val m = patterns.size
val compat = Array(m) { mutableListOf<Int>() }
for (i in 0 until m)
for (j in 0 until m)
if ((patterns[i] and patterns[j]) == 0)
compat[i].add(j)
var dp = IntArray(m) { 1 }
for (h in 1 until height) {
val ndp = IntArray(m)
for (i in 0 until m)
for (j in compat[i])
ndp[i] = (ndp[i] + dp[j]) % mod
dp = ndp
}
var ans = 0
for (x in dp) ans = (ans + x) % mod
return ans
}
}
Python
class Solution:
def buildWall(self, height: int, width: int, bricks: list[int]) -> int:
mod = 10**9+7
patterns = []
def dfs(pos, mask):
if pos == width:
patterns.append(mask)
return
for b in bricks:
if pos + b > width: continue
nmask = mask
if pos + b < width: nmask |= 1 << (pos + b)
dfs(pos + b, nmask)
dfs(0, 0)
m = len(patterns)
compat = [[] for _ in range(m)]
for i in range(m):
for j in range(m):
if patterns[i] & patterns[j] == 0:
compat[i].append(j)
dp = [1]*m
for _ in range(1, height):
ndp = [0]*m
for i in range(m):
for j in compat[i]:
ndp[i] = (ndp[i] + dp[j]) % mod
dp = ndp
return sum(dp) % mod
Rust
impl Solution {
pub fn build_wall(height: i32, width: i32, bricks: Vec<i32>) -> i32 {
let modv = 1_000_000_007;
let width = width as usize;
let mut patterns = vec![];
fn dfs(pos: usize, mask: usize, width: usize, bricks: &Vec<i32>, patterns: &mut Vec<usize>) {
if pos == width { patterns.push(mask); return; }
for &b in bricks {
let b = b as usize;
if pos + b > width { continue; }
let mut nmask = mask;
if pos + b < width { nmask |= 1 << (pos + b); }
dfs(pos + b, nmask, width, bricks, patterns);
}
}
dfs(0, 0, width, &bricks, &mut patterns);
let m = patterns.len();
let mut compat = vec![vec![]; m];
for i in 0..m {
for j in 0..m {
if patterns[i] & patterns[j] == 0 {
compat[i].push(j);
}
}
}
let mut dp = vec![1; m];
for _ in 1..height {
let mut ndp = vec![0; m];
for i in 0..m {
for &j in &compat[i] {
ndp[i] = (ndp[i] + dp[j]) % modv;
}
}
dp = ndp;
}
dp.iter().fold(0, |acc, &x| (acc + x) % modv)
}
}
TypeScript
class Solution {
buildWall(height: number, width: number, bricks: number[]): number {
const mod = 1_000_000_007
const patterns: number[] = []
function dfs(pos: number, mask: number) {
if (pos === width) { patterns.push(mask); return }
for (const b of bricks) {
if (pos + b > width) continue
let nmask = mask
if (pos + b < width) nmask |= 1 << (pos + b)
dfs(pos + b, nmask)
}
}
dfs(0, 0)
const m = patterns.length
const compat: number[][] = Array.from({length: m}, () => [])
for (let i = 0; i < m; i++)
for (let j = 0; j < m; j++)
if ((patterns[i] & patterns[j]) === 0)
compat[i].push(j)
let dp = new Array(m).fill(1)
for (let h = 1; h < height; h++) {
const ndp = new Array(m).fill(0)
for (let i = 0; i < m; i++)
for (const j of compat[i])
ndp[i] = (ndp[i] + dp[j]) % mod
dp = ndp
}
return dp.reduce((a, b) => (a + b) % mod, 0)
}
}
Complexity
- ⏰ Time complexity:
O(H * M^2), where H is height and M is the number of valid row patterns (exponential in width). - 🧺 Space complexity:
O(M^2), for compatibility and DP arrays.