problemhardalgorithmsleetcode-1411leetcode 1411leetcode1411

Number of Ways to Paint N × 3 Grid

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Number of Ways to Paint N × 3 Grid Problem

Problem

You have a grid of size n x 3 and you want to paint each cell of the grid with exactly one of the three colors: Red, Yellow, or Green while making sure that no two adjacent cells have the same color (i.e., no two cells that share vertical or horizontal sides have the same color).

Given n the number of rows of the grid, return the number of ways you can paint this grid. As the answer may grow large, the answer must be computed modulo 10^9 + 7.

Examples

Example 1:

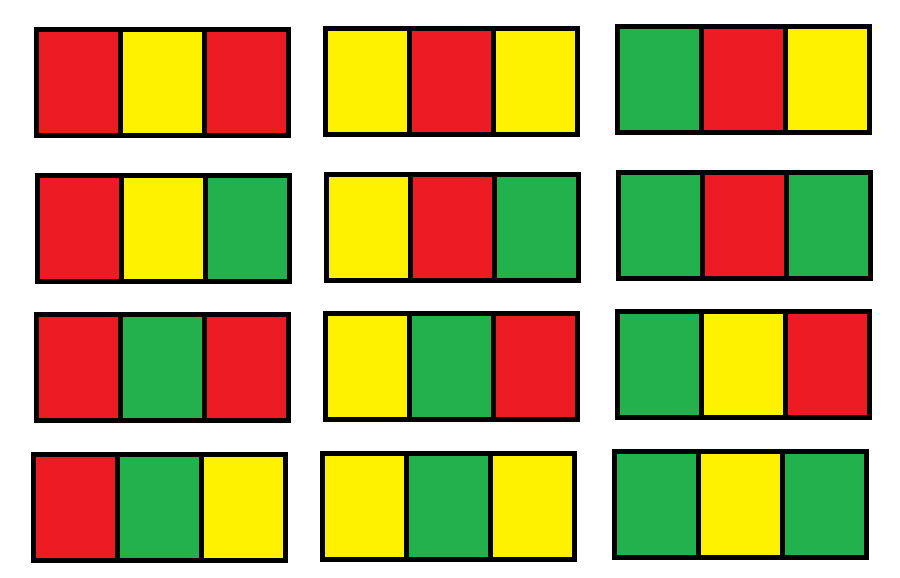
Input:
n = 1
Output:
 12
Explanation: There are 12 possible way to paint the grid as shown.

Example 2:

Input:
n = 5000
Output:
 30228214

Solution

Method 1 – Dynamic Programming

Intuition

Model the problem using two states for each row: the number of ways to paint the row with two color patterns (type1: all three colors different, type2: two colors same, but no adjacent same color). Use DP to propagate the count for each row.

Approach

  1. For n = 1, there are 6 ways for type1 (all different) and 6 ways for type2 (two same, but not adjacent), total 12.
  2. For each subsequent row, update type1 and type2 using recurrence relations based on previous row.
  3. Return the sum modulo 1e9+7.

Code

C++
class Solution {
public:
    int numOfWays(int n) {
        int MOD = 1e9+7;
        long a = 6, b = 6;
        for (int i = 2; i <= n; ++i) {
            long a_new = (2*a + 2*b) % MOD;
            long b_new = (2*a + 3*b) % MOD;
            a = a_new; b = b_new;
        }
        return (a + b) % MOD;
    }
};
Go
func numOfWays(n int) int {
    mod := int(1e9+7)
    a, b := 6, 6
    for i := 2; i <= n; i++ {
        a, b = (2*a+2*b)%mod, (2*a+3*b)%mod
    }
    return (a+b)%mod
}
Java
class Solution {
    public int numOfWays(int n) {
        int MOD = 1_000_000_007;
        long a = 6, b = 6;
        for (int i = 2; i <= n; ++i) {
            long a_new = (2*a + 2*b) % MOD;
            long b_new = (2*a + 3*b) % MOD;
            a = a_new; b = b_new;
        }
        return (int)((a + b) % MOD);
    }
}
Kotlin
class Solution {
    fun numOfWays(n: Int): Int {
        val MOD = 1_000_000_007
        var a = 6L; var b = 6L
        for (i in 2..n) {
            val aNew = (2*a + 2*b) % MOD
            val bNew = (2*a + 3*b) % MOD
            a = aNew; b = bNew
        }
        return ((a + b) % MOD).toInt()
    }
}
Python
class Solution:
    def numOfWays(self, n: int) -> int:
        MOD = 10**9+7
        a, b = 6, 6
        for _ in range(2, n+1):
            a, b = (2*a + 2*b) % MOD, (2*a + 3*b) % MOD
        return (a + b) % MOD
Rust
impl Solution {
    pub fn num_of_ways(n: i32) -> i32 {
        let mut a = 6i64;
        let mut b = 6i64;
        let m = 1_000_000_007i64;
        for _ in 2..=n {
            let a_new = (2*a + 2*b) % m;
            let b_new = (2*a + 3*b) % m;
            a = a_new; b = b_new;
        }
        ((a + b) % m) as i32
    }
}
TypeScript
class Solution {
    numOfWays(n: number): number {
        const MOD = 1e9+7;
        let a = 6, b = 6;
        for (let i = 2; i <= n; ++i) {
            const aNew = (2*a + 2*b) % MOD;
            const bNew = (2*a + 3*b) % MOD;
            a = aNew; b = bNew;
        }
        return (a + b) % MOD;
    }
}

Complexity

  • ⏰ Time complexity: O(n)
    • We iterate through n rows, updating two states at each step.
  • 🧺 Space complexity: O(1)
    • Only a constant number of variables are used for the DP states.

Comments