Problem

There are n houses in a village. We want to supply water for all the houses by building wells and laying pipes.

For each house i, we can either build a well inside it directly with cost wells[i - 1] (note the -1 due to 0-indexing), or pipe in water from another well to it. The costs to lay pipes between houses are given by the array pipes where each pipes[j] = [house1j, house2j, costj] represents the cost to connect house1j and house2j together using a pipe. Connections are bidirectional, and there could be multiple valid connections between the same two houses with different costs.

Return the minimum total cost to supply water to all houses.

Examples

Example 1:

1
2
3
4
5

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/1100-1199/1168.Optimize%20Water%20Distribution%20in%20a%20Village/images/1359_ex1.png)
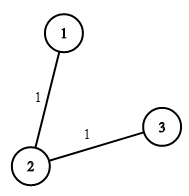
Input: n = 3, wells = [1,2,2], pipes = [[1,2,1],[2,3,1]]
Output: 3
Explanation: The image shows the costs of connecting houses using pipes.
The best strategy is to build a well in the first house with cost 1 and connect the other houses to it with cost 2 so the total cost is 3.

Example 2:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

Input: n = 2, wells = [1,1], pipes = [[1,2,1],[1,2,2]]
Output: 2
Explanation: We can supply water with cost two using one of the three options:
Option 1:
- Build a well inside house 1 with cost 1.
- Build a well inside house 2 with cost 1.
The total cost will be 2.
Option 2:
- Build a well inside house 1 with cost 1.
- Connect house 2 with house 1 with cost 1.
The total cost will be 2.
Option 3:
- Build a well inside house 2 with cost 1.
- Connect house 1 with house 2 with cost 1.
The total cost will be 2.
Note that we can connect houses 1 and 2 with cost 1 or with cost 2 but we will always choose **the cheapest option**.

Constraints:

  • 2 <= n <= 10^4
  • wells.length == n
  • 0 <= wells[i] <= 10^5
  • 1 <= pipes.length <= 10^4
  • pipes[j].length == 3
  • 1 <= house1j, house2j <= n
  • 0 <= costj <= 10^5
  • house1j != house2j

Solution

Method 1 – Minimum Spanning Tree (Prim’s or Kruskal’s Algorithm)

Intuition

We can model the problem as a graph where each house is a node. Building a well at house i is like connecting it to a virtual node 0 with cost wells[i-1]. All pipes are edges between houses. The minimum cost to supply water to all houses is the cost of the minimum spanning tree (MST) of this graph.

Approach

  1. Create a virtual node 0. For each house i, add an edge from 0 to i with cost wells[i-1].
  2. Add all pipes as edges between houses.
  3. Use Kruskal’s or Prim’s algorithm to find the MST and sum the costs.
  4. Return the total cost.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution {
public:
    int minCostToSupplyWater(int n, vector<int>& wells, vector<vector<int>>& pipes) {
        vector<vector<int>> edges;
        for (int i = 0; i < n; ++i) edges.push_back({0, i+1, wells[i]});
        for (auto& p : pipes) edges.push_back(p);
        sort(edges.begin(), edges.end(), [](auto& a, auto& b) { return a[2] < b[2]; });
        vector<int> par(n+1);
        iota(par.begin(), par.end(), 0);
        function<int(int)> find = [&](int x) { return par[x] == x ? x : par[x] = find(par[x]); };
        int ans = 0, cnt = 0;
        for (auto& e : edges) {
            int u = find(e[0]), v = find(e[1]);
            if (u != v) {
                par[u] = v;
                ans += e[2];
                if (++cnt == n) break;
            }
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

func minCostToSupplyWater(n int, wells []int, pipes [][]int) int {
    edges := make([][]int, 0, len(wells)+len(pipes))
    for i, w := range wells {
        edges = append(edges, []int{0, i+1, w})
    }
    edges = append(edges, pipes...)
    sort.Slice(edges, func(i, j int) bool { return edges[i][2] < edges[j][2] })
    par := make([]int, n+1)
    for i := range par { par[i] = i }
    var find func(int) int
    find = func(x int) int { if par[x] != x { par[x] = find(par[x]) }; return par[x] }
    ans, cnt := 0, 0
    for _, e := range edges {
        u, v := find(e[0]), find(e[1])
        if u != v {
            par[u] = v
            ans += e[2]
            cnt++
            if cnt == n { break }
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
    public int minCostToSupplyWater(int n, int[] wells, int[][] pipes) {
        List<int[]> edges = new ArrayList<>();
        for (int i = 0; i < n; i++) edges.add(new int[]{0, i+1, wells[i]});
        for (int[] p : pipes) edges.add(p);
        edges.sort(Comparator.comparingInt(a -> a[2]));
        int[] par = new int[n+1];
        for (int i = 0; i <= n; i++) par[i] = i;
        int ans = 0, cnt = 0;
        for (int[] e : edges) {
            int u = find(par, e[0]), v = find(par, e[1]);
            if (u != v) {
                par[u] = v;
                ans += e[2];
                if (++cnt == n) break;
            }
        }
        return ans;
    }
    private int find(int[] par, int x) {
        if (par[x] != x) par[x] = find(par, par[x]);
        return par[x];
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
    fun minCostToSupplyWater(n: Int, wells: IntArray, pipes: Array<IntArray>): Int {
        val edges = mutableListOf<IntArray>()
        for (i in wells.indices) edges.add(intArrayOf(0, i+1, wells[i]))
        edges.addAll(pipes)
        edges.sortBy { it[2] }
        val par = IntArray(n+1) { it }
        fun find(x: Int): Int = if (par[x] == x) x else { par[x] = find(par[x]); par[x] }
        var ans = 0; var cnt = 0
        for (e in edges) {
            val u = find(e[0]); val v = find(e[1])
            if (u != v) {
                par[u] = v
                ans += e[2]
                cnt++
                if (cnt == n) break
            }
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution:
    def minCostToSupplyWater(self, n: int, wells: list[int], pipes: list[list[int]]) -> int:
        edges = [[0, i+1, w] for i, w in enumerate(wells)] + pipes
        edges.sort(key=lambda x: x[2])
        par = list(range(n+1))
        def find(x: int) -> int:
            if par[x] != x:
                par[x] = find(par[x])
            return par[x]
        ans = cnt = 0
        for u, v, c in edges:
            fu, fv = find(u), find(v)
            if fu != fv:
                par[fu] = fv
                ans += c
                cnt += 1
                if cnt == n:
                    break
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

impl Solution {
    pub fn min_cost_to_supply_water(n: i32, wells: Vec<i32>, pipes: Vec<Vec<i32>>) -> i32 {
        let mut edges = Vec::with_capacity(wells.len() + pipes.len());
        for (i, &w) in wells.iter().enumerate() {
            edges.push(vec![0, (i+1) as i32, w]);
        }
        for p in pipes.iter() { edges.push(p.clone()); }
        edges.sort_by_key(|e| e[2]);
        let mut par: Vec<i32> = (0..=n).collect();
        fn find(par: &mut Vec<i32>, x: i32) -> i32 {
            if par[x as usize] != x {
                par[x as usize] = find(par, par[x as usize]);
            }
            par[x as usize]
        }
        let mut ans = 0;
        let mut cnt = 0;
        for e in edges {
            let u = find(&mut par, e[0]);
            let v = find(&mut par, e[1]);
            if u != v {
                par[u as usize] = v;
                ans += e[2];
                cnt += 1;
                if cnt == n { break; }
            }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution {
    minCostToSupplyWater(n: number, wells: number[], pipes: number[][]): number {
        let edges: number[][] = wells.map((w, i) => [0, i+1, w]).concat(pipes)
        edges.sort((a, b) => a[2] - b[2])
        let par: number[] = Array.from({length: n+1}, (_, i) => i)
        function find(x: number): number {
            if (par[x] !== x) par[x] = find(par[x])
            return par[x]
        }
        let ans = 0, cnt = 0
        for (let [u, v, c] of edges) {
            let fu = find(u), fv = find(v)
            if (fu !== fv) {
                par[fu] = fv
                ans += c
                cnt++
                if (cnt === n) break
            }
        }
        return ans
    }
}

Complexity

  • ⏰ Time complexity: O((n + m) log (n + m)), where n is the number of houses and m is the number of pipes. Sorting all edges dominates.
  • 🧺 Space complexity: O(n + m), for storing all edges and the union-find structure.